MATLAB实现将函数/序列进行周期延拓

原函数

假设我们有这么一个函数

x(n)=3cos(0.125πn+0.2π)+2sin(0.25πn+0.1π)
n为0到15的整数

这是他的函数图像，如何将其进行周期化

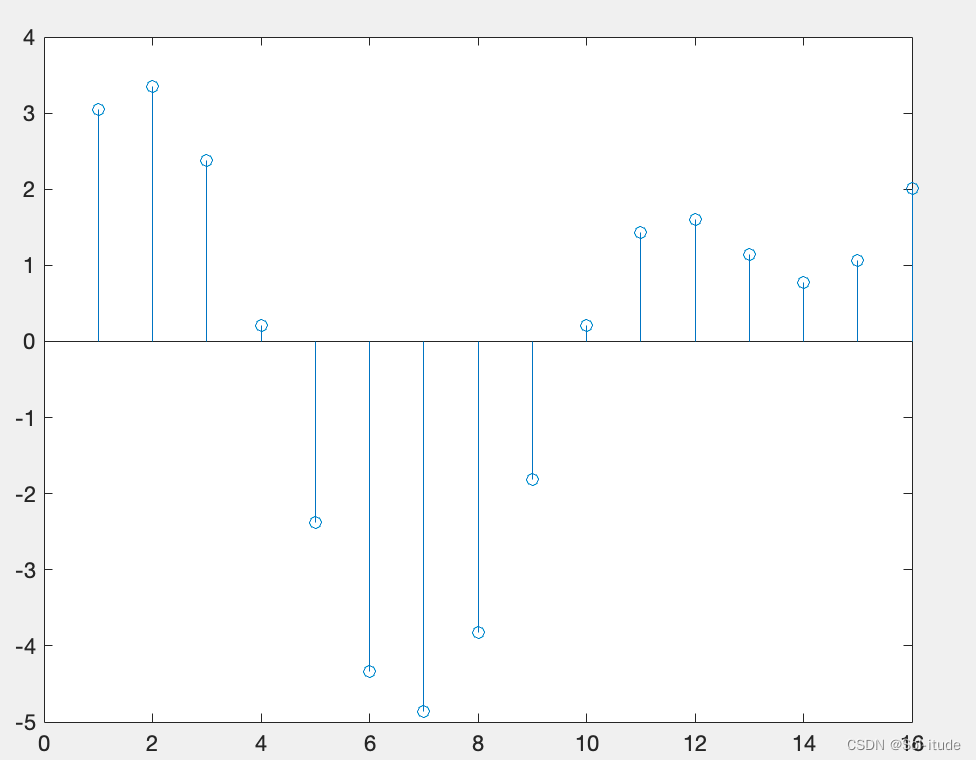
我在MATLAB中文论坛看到了一个很巧妙的方法

b = mod(a,m)

b = mod(a,m) 返回 a 除以 m 后的余数，其中 a 是被除数，m 是除数。此函数通常称为取模运算，表达式为 b = a-m.*floor(a./m)。mod 函数遵从 mod(a,0) 返回 a 的约定。

例子

b = mod(23,5)

b=3,其实就是一个取余的运算

周期化函数

那么我们转变一下思路，将函数的自变量进行一个延展，再用其周期进行取余，不就变成了周期函数

假如x要以16为周期，延拓4个周期

n2=0:80
n22=mod(n2,15);
x2=3*cos(0.125*pi*n22+0.2*pi)+2*sin(0.25*pi*n22+0.1*pi);
stem(x2)

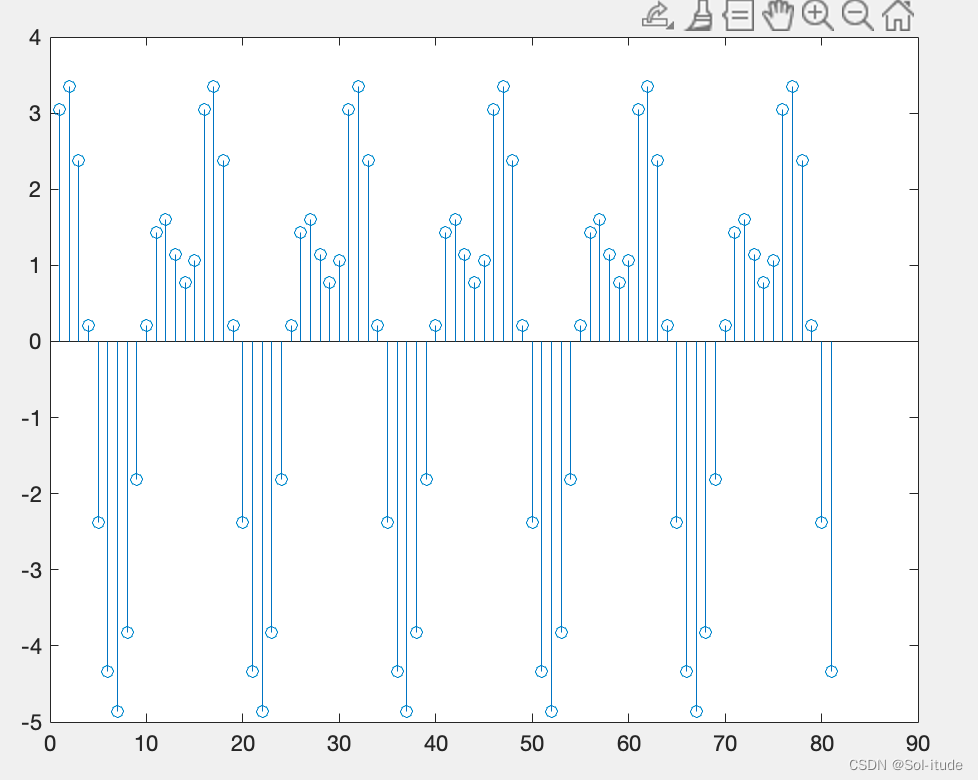
就算出来了

完整代码

画函数原来的图

n1=0:15;
x1=3*cos(0.125*pi*n1+0.2*pi)+2*sin(0.25*pi*n1+0.1*pi);
stem(x1)

画周期函数的图

n2=0:80
n22=mod(n2,15);
x2=3*cos(0.125*pi*n22+0.2*pi)+2*sin(0.25*pi*n22+0.1*pi);
stem(x2)

局限性

因为在这道题中，n只提供了正值，就导致负半轴的延拓必须通过修改n的值来实现
例如：
如果想将本文中的序列延拓到四个周期
，正负各一半，就要这么写

n1=0:15;
x1=3*cos(0.125*pi*n1+0.2*pi)+2*sin(0.25*pi*n1+0.1*pi);
subplot(2,1,1);
stem(n1,x1)

n2=0:63;
n22=mod(n2,15);
x2=3*cos(0.125*pi*n22+0.2*pi)+2*sin(0.25*pi*n22+0.1*pi);
n3=-32:31;
subplot(2,1,2);
stem(n3,x2)

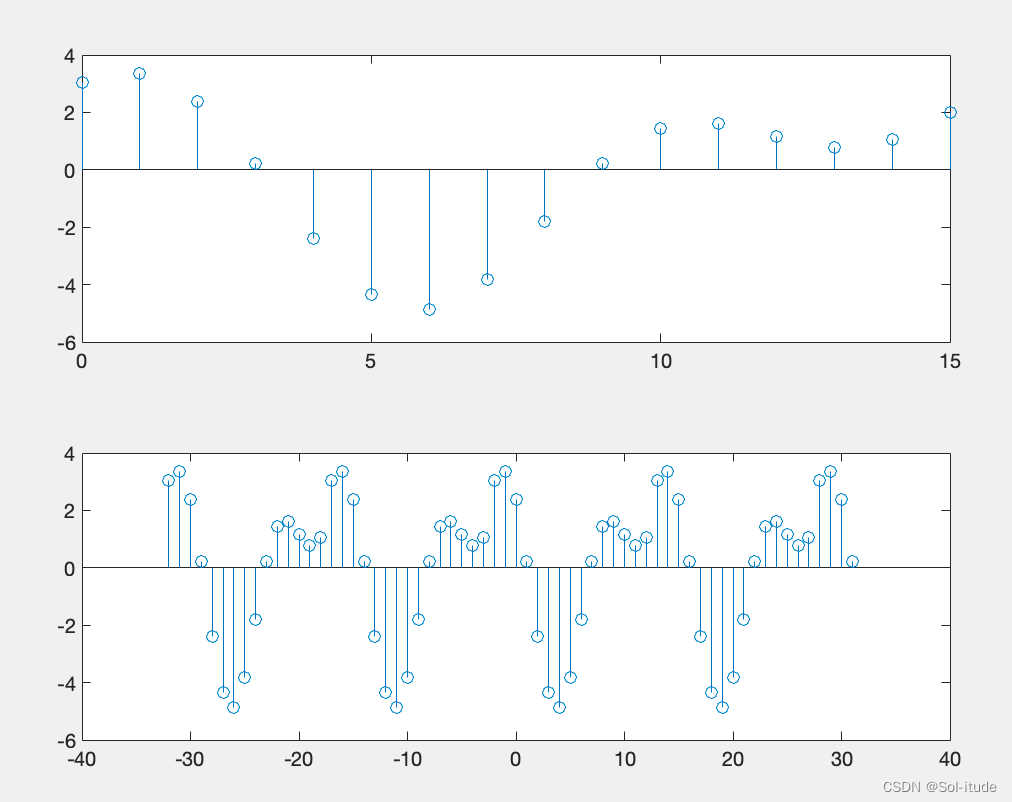
只能实现有限周期的延拓

最后

以上就是平常保温杯为你收集整理的MATLAB实现将函数/序列进行周期延拓的全部内容，希望文章能够帮你解决MATLAB实现将函数/序列进行周期延拓所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。