离散时间信号——序列的基本运算及matlab实现

前言

本篇文章主要介绍数字信号处理内容中的离散信号序列的基本运算，如：序列相加、序列相乘、倍率、移位、折叠、样本和等内容及matlab代码的实现。

提示：以下是本篇文章正文内容，下面MATLAB已亲测有效

一、什么是离散时间信号？

1、离散时间信号

信号可分为模拟信号和数字信号。模拟信号可表示为x(t),表示连续时间，，例如生活中的声音信号。而数字信号可以用x(n)来表示，代表时间的离散时刻，因此也称为离散时间信号，它的表示方法是一个有序的数字序列。
离散时间信号：时间为离散变量，幅度为连续变化的变量。

2、数字信号处理系统

数字信号处理系统基本由以下部分组成:前端模拟信号接收装置、抗混叠滤波、A/D转换装置、数字信号处理模块(DSP)、D/A转换装置、平滑滤波组成。

二、序列的基本运算

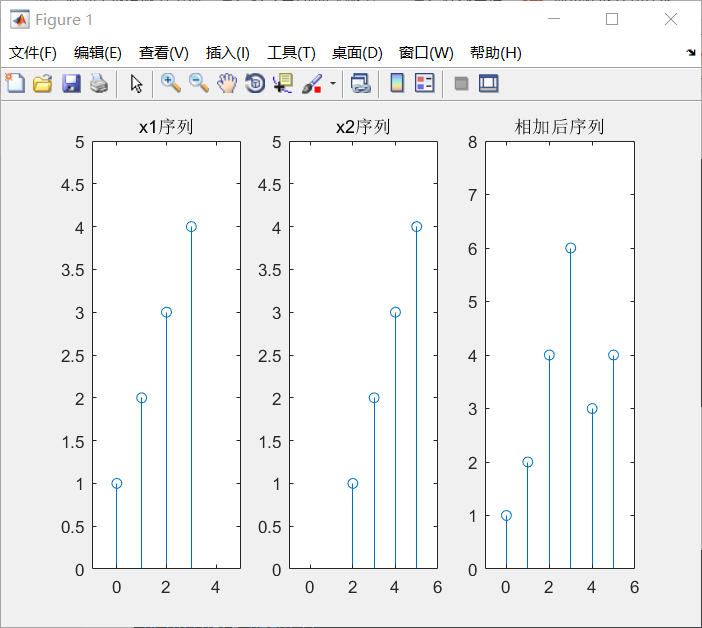
1.序列相加

序列相加是一个对应样本与样本之间的相加。
自定义sigadd函数演示运算：

function [y,n] = sigadd(x1,n1,x2,n2)
%实现序列相加
% 实现y(n)=x1(n)+x2(n)
% [y,n ]=sigadd(x1 ,n1,x2,n2)
n = min(min(n1),min(n2)):max(max(n1),max(n2));
y1 = zeros(1,length(n));
y2=y1;

y1 (find( (n>=min (n1) ) & (n<=max (n1) )==1) )=x1 ;
y2 (find( (n>=min (n2) ) & (n<=max (n2) )==1) )=x2 ;

y=y1+y2;

end

调用该函数

n1=[0 1 2 3];
x1=[1 2 3 4];

n2=[2 3 4 5];
x2=[1 2 3 4];

subplot(131);
stem(n1,x1);
axis([-1 5,0 5]);
title('x1序列');

subplot(132);
stem(n2,x2);
axis([-1 6,0 5]);
title('x2序列');

[y,n]=sigadd(x1,n1,x2,n2);

subplot(133);
stem(n,y);
axis([-1 6,0 8]);
title('相加后序列');

结果是正确的

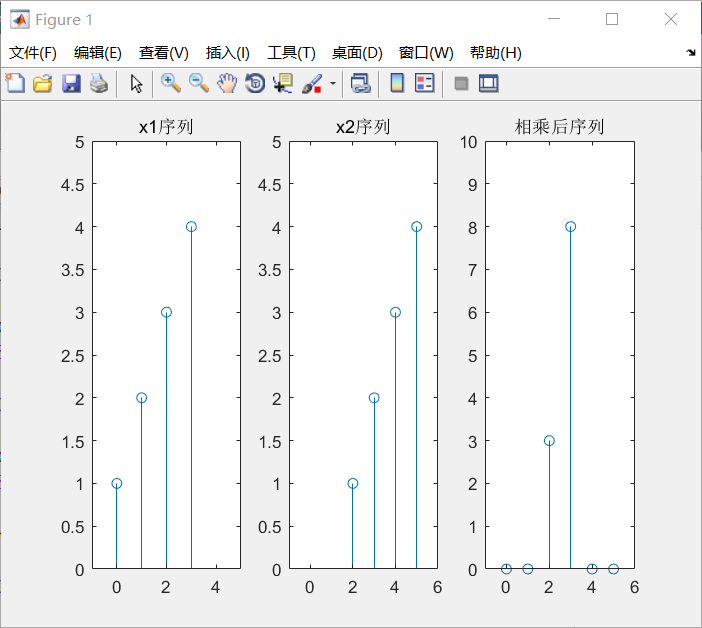
2.序列相乘

序列相乘是对应采样点之间的相乘（点乘）
自定义sigmuti函数演示运算：

function [y,n] = sigmuti(x1,n1,x2,n2)
% 实现y(n)=x1(n)*x2(n)
% [y,n ]=sigmuti(x1 ,n1,x2,n2)
n = min(min(n1),min(n2)):max(max(n1),max(n2));
y1 = zeros(1,length(n));
y2=y1;

y1 (find( (n>=min (n1) ) & (n<=max (n1) )==1) )=x1 ;
y2 (find( (n>=min (n2) ) & (n<=max (n2) )==1) )=x2 ;

y=y1.*y2;
end

调用该函数

n1=[0 1 2 3];
x1=[1 2 3 4];

n2=[2 3 4 5];
x2=[1 2 3 4];

subplot(131);
stem(n1,x1);
axis([-1 5,0 5]);
title('x1序列');

subplot(132);
stem(n2,x2);
axis([-1 6,0 5]);
title('x2序列');

[y,n]=sigmuti(x1,n1,x2,n2);

subplot(133);
stem(n,y);
axis([-1 6,0 10]);
title('相乘后序列');

结果图

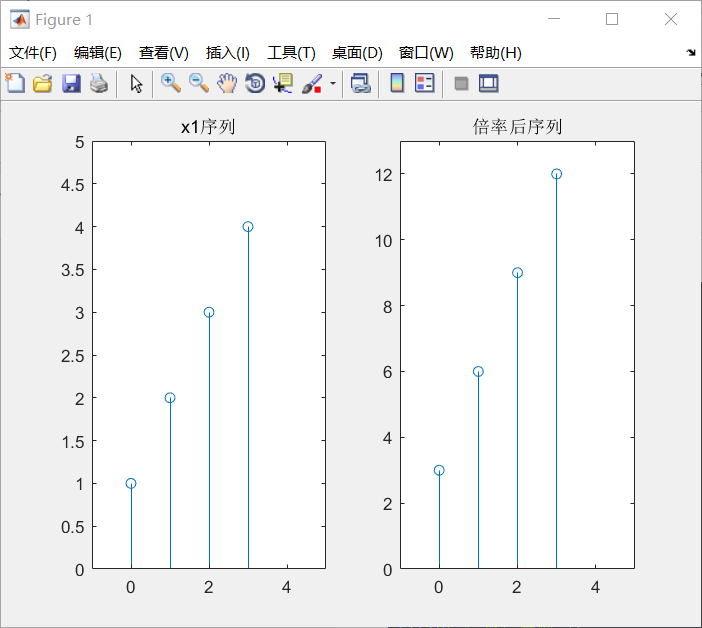
3、序列倍率

这个运算很简单，每一个采样值都乘以倍数a就可以了。
自定义sigdouble函数演示运算：

function [y,n] = sigdouble(x1,n1,a)
%sigdouble 序列倍率
%   在此运算中，
% 每个采样值乘以一个常数a。
% a{x(n)}= {ax(n)}
% 在MATLAB中可用算术运算符“*”来实现倍率运算。
n=n1;
y=a*x1;
end

调用运行

n1=[0 1 2 3];
x1=[1 2 3 4];
a=3;        %倍率
[y,n]=sigdouble(x1,n1,a);
subplot(121);
stem(n1,x1);
axis([-1 5,0 5]);
title('x1序列');

subplot(122);
stem(n,y);
axis([-1 5,0 13]);
title('倍率后序列');

结果图

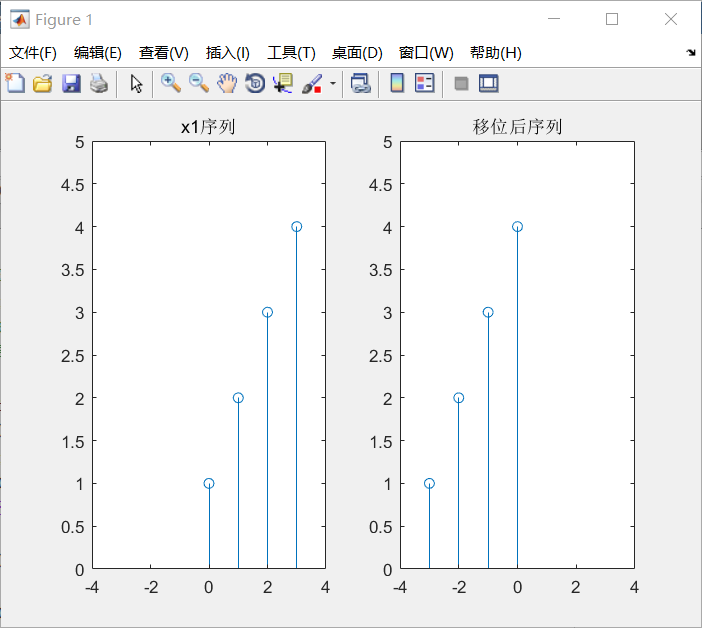
4、序列移位

通过移位运算，每个采样值都向右移动k个单位（k正为右，负为左）。
移位后：y（n）={x（n-k）}
自定义sigfold函数演示运算：

function [y,n] = sigshift(x,m,n0)
%实现y(n)=x(n-n0)
%移位--在此运算中，x (n)的每一个样本都移动n0个周期，移位后的序列y (n)如下。

n=m+n0;
y=x;


end

调用运行：

n1=[0 1 2 3];
x1=[1 2 3 4];
a=-3;        %向左平移3个单位
[y,n]=sigshift(x1,n1,a);
subplot(121);
stem(n1,x1);
axis([-4 4,0 5]);
title('x1序列');

subplot(122);
stem(n,y);
axis([-4 4,0 5]);
title('移位后序列');

结果图：

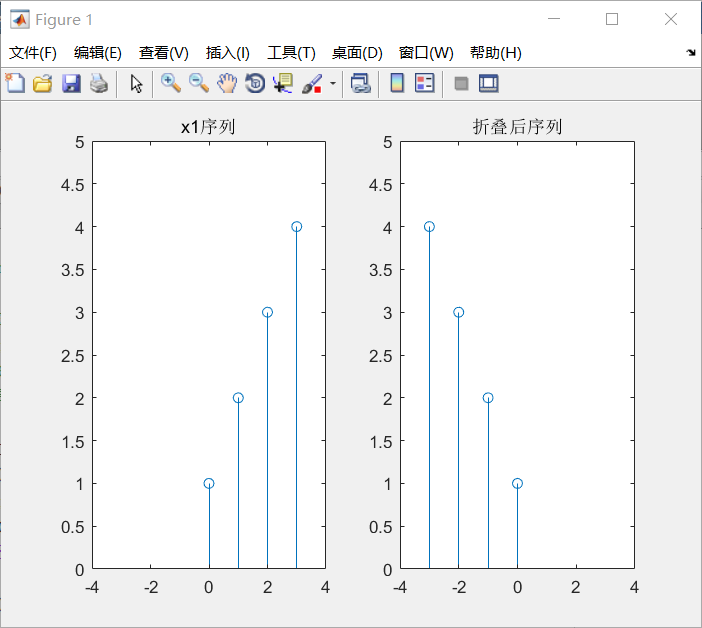
5、序列折叠

通过折叠运算，使得采样值每个样本按照n=0翻转
自定义sigfold函数演示运行：

function [y,n] = sigfold(x,n0)
%序列折叠运算
%在此运算中，x (n)的每个样本都对n= o翻转，得到一个折叠后的序列y(n)
%y(n)={x(-n)}
y=fliplr(x);
n=-max(n0):-min(n0);  

end

调用运行：

n1=[0 1 2 3];
x1=[1 2 3 4];
[y,n]=sigfold(x1,n1);
subplot(121);
stem(n1,x1);
axis([-4 4,0 5]);
title('x1序列');

subplot(122);
stem(n,y);
axis([-4 4,0 5]);
title('折叠后序列');

结果图：

总结

至此，序列的基本运算就介绍完了。往后我会持续更新信号处理的其他内容，欢迎志同道合的同仁批评指正，一起探讨经验。
QQ：2395277840
作者：草莓味的徐大力

最后

以上就是忧伤金针菇为你收集整理的信号处理第一式——离散信号序列的基本运算及MATLAB实现离散时间信号——序列的基本运算及matlab实现前言一、什么是离散时间信号？二、序列的基本运算总结的全部内容，希望文章能够帮你解决信号处理第一式——离散信号序列的基本运算及MATLAB实现离散时间信号——序列的基本运算及matlab实现前言一、什么是离散时间信号？二、序列的基本运算总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。