滤波器的设计
引言
对实际的控制系统而言,采集到的原始信号往往是有噪声的,而噪声往往会对系统的稳定性能产生隐患;或为了提取有用的控制信号,滤除不必要的频域成分,数字滤波技术必不可少。
滤波器的分类
按频率特性分类:高通、低通、带通和带阻;
按冲激响应特性分类:
FIR滤波器:有限冲激响应,滤波器的输出只与当前输入和有限历史输入有关,无反馈回路,不存在不稳定的问题,其传递函数只有零点,这种滤波器的冲激响应时间是有限的,在一定时刻后滤波器的输出会为0;
IIR滤波器:无限冲激响应,滤波器的输出不仅与当前和历史输入有关,还和历史输出有关;有反馈,传递函数既有零点也有极点,其冲击序列是无限的时间序列,随着时间的增长,输出可能会变小,但不会为0;
滤波器的截止频率选取
为了确定滤波器的截止频率,我们使用傅里叶变换来确定待滤波信号中的各频率分量信号占比;在matlab中调用快速傅里叶变换函数可以很方便地进行频谱分析(此处频率以赫兹为单位);ps:一般控制系统的频域分析以rad/s为单位,如bode图
matlab进行频谱分析的示例代码如下:(输入信号由自己创建)
%使用simulink输出信号使用快速傅里叶变换进行频谱分析
num=144;
T=10;
Fs=num/T;
Ts=T/num;
t= Ts:Ts:T;%采样步长
y= sim;
N=length(t); %样点个数
plot(t,y);
fs=Fs;%采样频率
df=fs/(N-1) ;%分辨率
f=(0:N-1)*df;%其中每点的频率
Y=fft(y)/N*2;%真实的幅值
%Y=fftshift(Y);
figure(2)
plot(f,abs(Y));
axis([0 fs/2 -inf inf]);
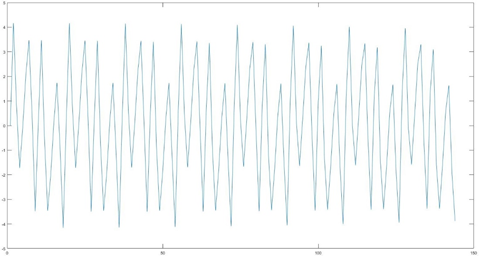
这张是原始信号的波形。
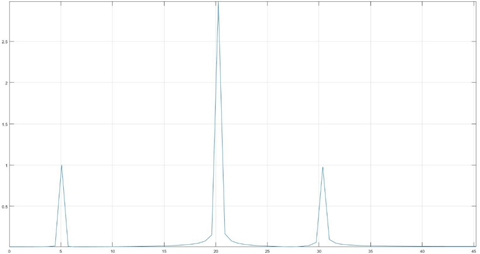
这张是傅里叶变换后的的频域表示(横坐标为频率值,纵坐标为各谐波分量的幅值)。
从频谱分析的结果来看,快速傅里叶变换能准确分离出不同频段的信号和其幅值,值得注意的是,由于香农采样定理,频谱图中频率高于采样频率一半的信号不能完全复现(故频谱只能分析频率在采样频率一半以下的信号)
有了输入信号的频谱图我们便可以根据自己的需要以及信号的频谱特性来确定截止频率,以便得到自己想要的频率范围的信号。
注意:在控制系统的反馈中,一般会结合被控对象的带宽来设置反馈信号的滤波器截止频率,高于系统带宽的信号往往是无意义的噪声(因为系统不能响应高于带宽的信号);
一般来说,宏观机械系统的带宽在50Hz以下,微机电系统可以达到100KHz,电路系统的带宽可达100MHz甚至10GHz以上。
滤波器的波德图
FIR滤波器:
从最基本的滑动均值滤波说起:
以四阶滑动均值滤波为例,离散域传递函数:(1+z-1+z-2+z^-3)/4,从离散域分析,这是一个纯零点系统,无反馈;
我们可以在matlab中画出该离散传递函数的波德图:
方法如下:
num=[1 2 3 4];%离散域传递函数形式:(1+2z^-1+3z^-2+4z^-3)/10
den=[10];
dbode(num,den,0.001)%假设采样频率为1000hz
grid on
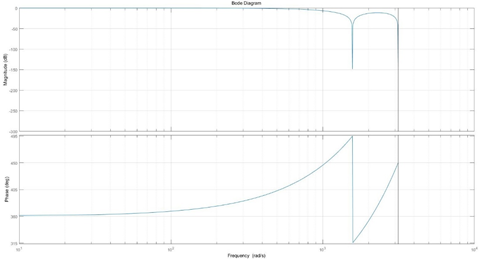
从波德图可以看出,这是一个低通滤波系统,截至频率在110hz左右(-3dB处);截止频率为Fs/n。其中Fs为采样频率。截至频率与采样频率相差越大,滤波器的阶数越高。(如下,采样频率1000hz,截止频率20hz,得到的滤波器127阶)
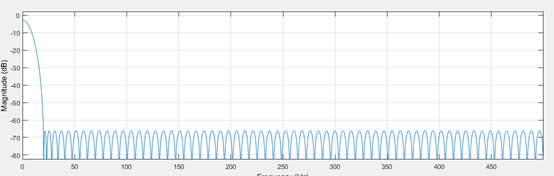
FIR由于只有前馈通道,没有反馈,可以不担心稳定性问题,这使得它在处理高速信号的时候具有优势。但是,FIR是非常消耗硬件资源的。使用硬件实现和代码实现均过于繁琐。
IIR滤波器:
反馈系统,最简单的例子是惯性环节;1/Ts+1,这是一个截止频率w约等于1/T的低通滤波器,但是惯性滤波的相位滞后比较严重,幅值曲线下降的也不够快,这时就需要更为高级的滤波器设计方法,如巴特沃斯和切比雪夫滤波器;下图为惯性环节的波德图:
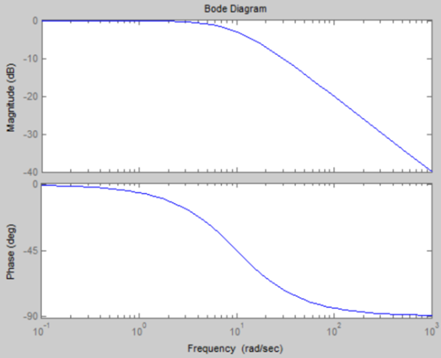
将滤波器的传递函数表示离散化(欧拉法、双线性变换法)得到差分方程,即可在嵌入式中实现;在具有相同的截止频率时,IIR滤波器的阶数更低。使用matlab自带的fdatool工具箱,选择采样频率和截止频率即可设计需要的FIR,IIR滤波器,能直接给出差分方程形式的表示,直接使用即可。
但是IIR是反馈系统,在高速的信号处理中,即使是使用并行实现,由于计算延迟和有限字长来造成的稳定性仍然是非常有挑战的。
最后
以上就是含蓄书本最近收集整理的关于滤波器的设计(一)的全部内容,更多相关滤波器内容请搜索靠谱客的其他文章。








发表评论 取消回复