PID参数 Ziegler-Nichols基于时域响应曲线的整定 反应曲线法

PID控制器是工业过程控制中广泛采用的一种控制器，其中，P、I、D分别为比例（Proportion）、积分（Integral）、微分（Differential）的简写；将偏差的比例、积分和微分通过线性组合构成控制量，用该控制量对受控对象进行控制，称为PID算法 。

其传递关系为：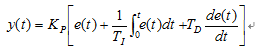

控制器的传递函数可写为：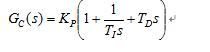

差分方程为：

其中KP、KI、KD分别为比例系数、积分系数、微分系数。

比例系数KP ：反应系统当前最基本的误差，系数大，可以加快调节，减小误差，但是过大的比例使系统稳定性下降，甚至造成系统的不稳定。

积分系数KI  ：反应系统的累计误差，使系统消除稳态误差，提高无差度，只要有误差，积分调节就会起作用。

微分系数KD ：反应系统误差的变化率，具有预见性，们可以预见偏差的变化趋势，产生超前的控制效果。因此可以改善系统的动态性能。但是微分对噪声有放大作用，会减弱系统的抗干扰性。

（一）PID控制器参数整定的方法有很多，概括起来主要有两大类：一是理论计算整定法，二是通过在线实验的工程整定法。

1. 理论计算整定法

它主要是依据被控对象准确的数学模型，经过理论计算确定控制器参数。这种方法一般较难做到，同时，得到的计算数据未必可以直接使用，还必须通过工程实际进行调整和修改。

  2.工程整定法

它不需要得到过程模型，主要依赖工程经验，在控制系统的试验中直接进行参数整定。方法简单实用，计算简便且易于掌握，可以解决一般的实际问题，在工程实际中被广泛采用。PID控制器参数的工程整定法，主要有临界比例度法（又称稳定边界法）、反应曲线法和4:1衰减法。其共同点都是通过实验，然后按照工程经验公式对控制器参数进行整定。然而，无论采用哪一种方法整定所得到的控制参数，都需要在实际运行中进行最后的调整与完善。
2.1试凑法就是通过仿真或实际运行，观察系统对典型输入作用的响应曲线，根据各控制参数对系统的影响，反复调节试凑，直到满意为止，从而确定PID参数。
  参数整定找最佳，从小到大顺序查，
  先是比例后积分，最后再把微分加，
  曲线振荡很频繁，比例度盘要放大，
  曲线漂浮绕大湾，比例度盘往小扳，
  曲线偏离回复慢，积分时间往下降，
  曲线波动周期长，积分时间再加长，
  曲线振荡频率快，先把微分降下来，
  动差大来波动慢，微分时间应加长，
  理想曲线两个波，前高后低四比一，
  一看二调多分析，调节质量不会低

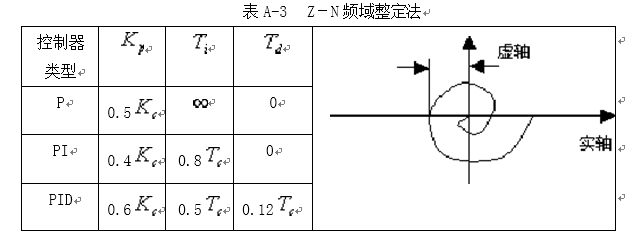
2.2 Ziegler-Nichols方法 已经发展成为一种在参数设定中，处于经验和计算法之间的中间方法。这种方法可以为控制器确定非常精确的参数，在此之后也可进行微调。
Ziegler-Nichols基于时域响应曲线的整定
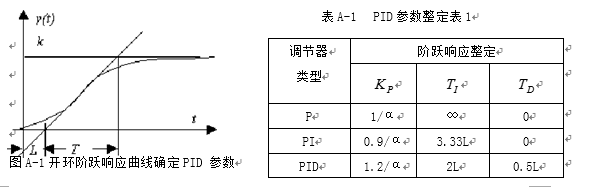
      1反应曲线法：用阶跃响应曲线来整定控制器的参数。
设想对被控对象(开环系统)施加一个阶跃信号，通过实验方法，测出其响应信号，根据这条阶跃响应曲线定出一些能反映控制对象动态特性的参数。如图所示，以曲线的拐点作一条切线得到三个参数：K是控制对象的增益，L是等效滞后时间，T是等效滞后时间常数。则输出信号可由图中的形状近似确定参数K，L和T（或α） ，其中 。如果获得了参数K，L和T（或α） 后，则可根据表A-1确定PID控制器的有关参数。

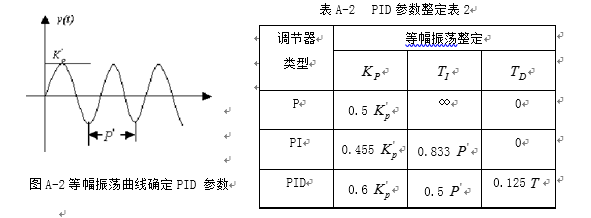
    2稳定边界法：用系统的等幅振荡曲线来整定控制器的参数。

先测出系统处于闭环状态下的对象的等幅振荡曲线，根据等幅振荡曲线定出一些能反映控制对象动态特性的参数。设系统为只有比例控制的闭环系统，则当KP增大时，闭环系统若能产生等幅振荡，如测出其振幅kp'和振荡周期p',然后由表A-2整定PID参数。

上述二法亦适用于系统模型已知的系统。但是此二法在应用中也有约束，因为许多系统并不与上述系统匹配，例如第一法无法应于开环传递中含积分项的系统，第二法就无法直接应用于二阶系统。如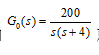就无法利用Ziegler-Nichols法进行整定。

Ziegler-Nichols基于频域法的整定

如果实验数据是由频率响应得到的，则可先画出其对应的Nyquist图，从图中可以容易得到系统的剪切频率 与系统的极限增益 ，若令 ，同样我们从表3-3给出的经验公式可以得到PID控制器对应的参数。事实上，此法即时域法的第二法。

（二）选用Ziegler-Nichols基于时域响应曲线的整定反应曲线法
已知受控对象为传递函数 
传递函数在阶跃信号激励下测出其响应信号，根据这条阶跃响应曲线定出一些能反映控制对象动态特性的参数。如图 4所示，以曲线的拐点作一条切线得到三个参数

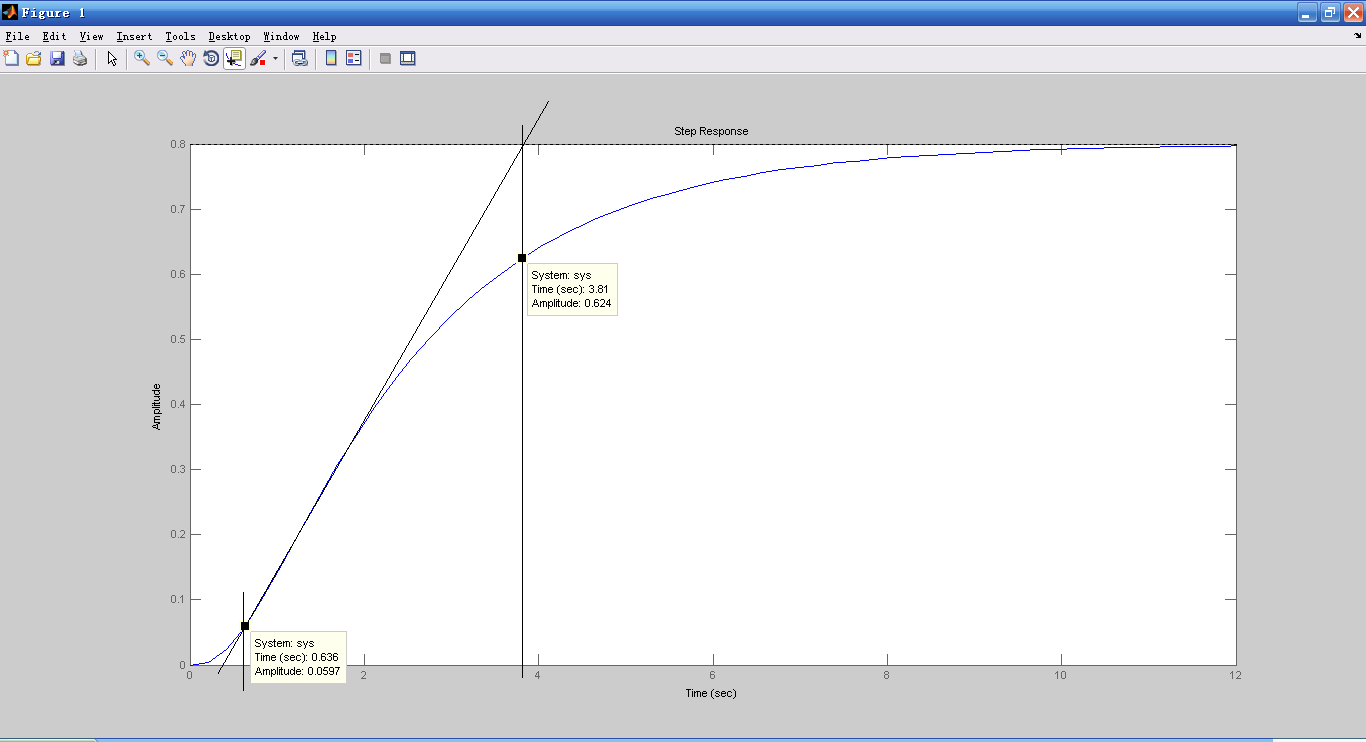
图 4开环阶跃响应曲线确定PID 参数

由图可知，取L=0.6 T=3.186 k =0.8000。于读图存在误差，因此参数仍需整定。已知对象的K、L 和T 值后,根据Ziegler — Nichols整定公式编写一个MATLAB函数

clc;clear

s=tf('s');clc;clear;

 num=[8];

den=conv([1 5],conv([1 2],[2 1]));

 G=tf(num,den)

 step(G,15);;hold on

 k=dcgain(num,den)

 L=0.6; T=3.186 ;K =0.8;

 a=K*L/T

PIDKp=1.2*T/(K*L); 

PIDTi=2*L;

PIDTd=0.5*L;

PIDG=PIDKp*(1+1/(PIDTi*s)+PIDTd*s)

step(feedback(PIDG*G,1)),hold on     

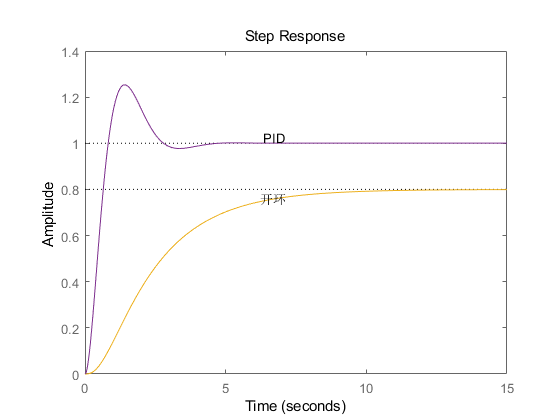
最后

以上就是含蓄小丸子为你收集整理的PID参数 Ziegler-Nichols基于时域响应曲线的整定 反应曲线法的全部内容，希望文章能够帮你解决PID参数 Ziegler-Nichols基于时域响应曲线的整定 反应曲线法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。