MATLAB信号处理——信号的变换（5）2-5频域采样

69 阅读 0 评论 46 点赞

我是靠谱客的博主妩媚鸭子，最近开发中收集的这篇文章主要介绍MATLAB信号处理——信号的变换（5）2-5频域采样，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

2-5频域采样

对于有限时宽序列x(n)的周期连续频谱X( n)进行均匀取样，当一个周期内的取样点数N大于或至少等于x (n)的有限时宽时，则有可能从频谱样点X(k)中无失真地恢复原来的周期连续频谱。如果已知一个信号的频谱，只要符合频域取样定理，对它进行频率取样，则有可能利用数字的方法求得相应的信号。

1.混叠失真

根据前面提到的采样定理，我们要求fs>2f，如果不满足这个条件，就会产生频域响应的周期延伸分量重叠现象，即频率响应的混叠失真。

针对混叠失真，我们可以提高采样频率，即减小采样间隔，也可以采用抗混滤波器。

2.频谱泄露

实际情况下，我们取的信号都是有限长的，即对原始信号序列做加窗处理使其成为有限长，然而使用加窗函数，就相当于时域相乘，频域进行卷积处理，此时频谱中除了我们需要的主瓣外，还有多余的旁瓣，这个旁瓣就是频谱泄露。

针对频谱失真，我们要改变调整窗函数，或者加长截取的时间段。

3.栅栏效应

栅栏效应是指离散傅里叶变换计算的频谱被限制在基频整数倍处，只能在相应离散点处看到输出的现象。栅栏效应是因为DFT计算的频谱被限制在基频的整数倍而不可能将频谱视为一个连续函数而产生的。就一定意义而言，栅栏效应表现为用DFT计算整个频谱时，就好像通过一个“栅栏”来观看一个图景一样，只能在离散点的地方看到真实图景。

针对栅栏效应，增加频域抽样点数N，同时在不改变时域数据的情况下，在时域数据末端添加一些零值点，使得谱线更密，这样就可以减小栅栏效应，观察到原来看不到的频谱分量。注意，该方法通过补零来增加N，此时采样频率f(s)会随之成正比上升，又由于频率分辨率F=f(s)/N，频率分辨率不改变，也就是说，补零不改变频率分辨率。

4.频率分辨率

频率分辨率是指将两个相邻谱峰分开的能力。实际应用时，可以将频率分辨率理解为频谱图中，在频率轴（频谱图的水平轴)）上得到的最小频率间隔如果采样频率为fs，采样时间间隔为t，采样点数为N，采样时间为t（完成一组样本的采集所需要的时间），则频率分辨率为：f=fs/N=1/t。

增大分辨率只有通过加大取样点N，但不能是补零而增加的。

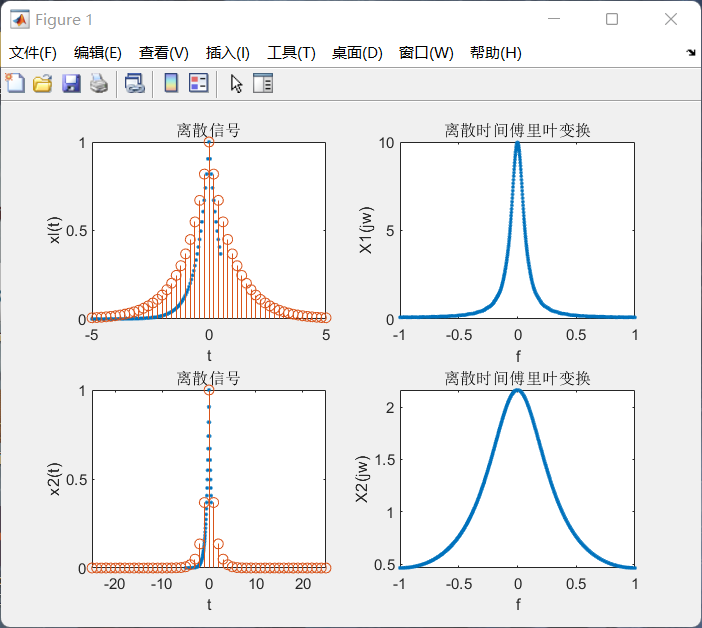
例1：已知模拟信号X(k),采样频率分别取5000Hz和1000Hz时，绘制出其傅里叶变换图。

clear all
Dt = 0.00005;
t = -0.005:Dt:0.0005;
xa = exp(-2000*abs(t));
Ts = 0.0002;
n = -25:1:25;
x = exp(-1000*abs(n*Ts));
K = 500;
k = 0:1:K;
w = pi*k/K;
X = x*exp(-j*n'*w);
X = real(X);
w = [ -fliplr(w),w(2:501)];
X = [fliplr(X),X(2:501)];
figure
subplot(221);
plot(t*1000,xa,'.');
ylabel('xl(t)');
xlabel('t');
title('离散信号');
hold on;
stem(n*Ts*1000,x);
hold off;
subplot(222);
plot(w/pi,X,'.');
ylabel('X1(jw)');
xlabel('f');
title('离散时间傅里叶变换');
Ts = 0.001;
n = -25:1:25;
x = exp(-1000*abs(n*Ts));
K = 500;
k = 0:1:K;
w = pi*k/K;
X = x*exp(-j*n'*w);
X = real(X);
w = [ -fliplr(w),w(2:501)];
X = [fliplr(X),X(2:501)];
subplot(223)
plot(t*1000,xa,'.');
ylabel('x2(t)');
xlabel('t');
title('离散信号');
hold on;
stem(n*Ts*1000,x);
hold off;
subplot(224)
plot(w/pi,X,'.');
ylabel('X2(jw)');
xlabel('f');
title('离散时间傅里叶变换');