在处理数据的时候,一般会进行数据拟合,这时候免不了会有噪点,从而造成图像上的“飞点”。幸好Matlab自带一个平滑函数smooth,笔者也是最近才晓得,做点笔记。
在Matlab Command Windows 中输入:
doc smooth
弹出来帮助文档,下面跟着帮助文档,记点有用的。
一、预备知识
有关平滑的算法又叫滤波算法,滤波是什么意思?百度百科中写道:滤波(Wave filtering)是将信号中特定波段频率滤除的操作,是抑制和防止干扰的一项重要措施,滤波分为经典滤波和现代滤波。“滤”这个字让我想起了老妈在家里用的面粉筛

(图片来源于网络)就是过滤杂质的。把噪点想象成“杂质”,那么滤波的意思就显而易见了。
1、滑动平均滤波
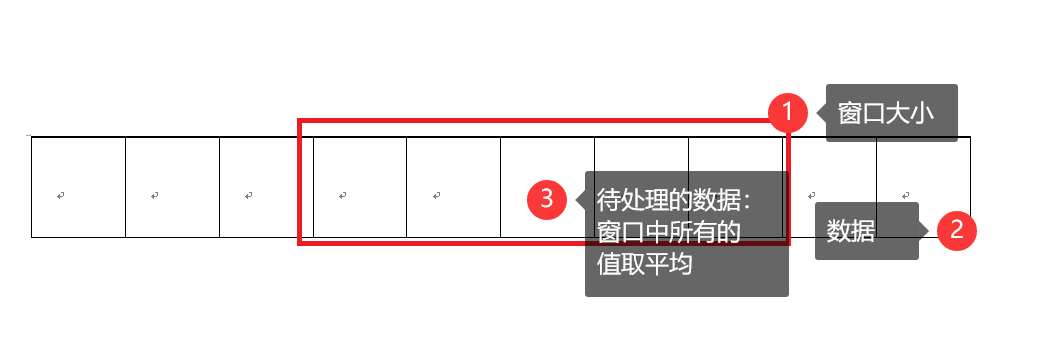
上图简单示意了滑动平均的思想,需要注意以下几点:
- 待处理的数据是一个一行或一列的向量,若不是,则将其看作是(顺序按存储顺序,matlab中)
- 窗口大小需是奇数,待处理的是中间那个数据
- 边缘数据,凑不够窗口大小个数的数据,能凑几个凑几个。
若窗口大小为5,则公式如下:
yy(1) = y(1)
yy(2) = (y(1) + y(2) + y(3))/3
yy(3) = (y(1) + y(2) + y(3) + y(4) + y(5))/5
yy(4) = (y(2) + y(3) + y(4) + y(5) + y(6))/5
...
2、其他平滑算法
如果理解滑动平均算法的话,其他算法也就好理解了。滑动平均算法可以看作和[1/n 1/n .. 1/n]做卷积(相乘相加),其他算法:
- 一次:一个一次的卷积函数,自变量为参与数与代求数的距离
- 二次及多次:卷积函数次数不同而已;值得注意的一点是窗口大小要大于卷积函数次数。
- 滑动平均算法可以看作是卷积函数是零次(常数)函数,因为里面不涉及自变量(参与数于代求数的距离)或者说自变量次数为0
3、gpuArray
就是将数据存储在GPU上面,可以加快计算效率,笔者曾经看到过一些GPU、CUP方面的知识并做了点总结,读者感兴趣可以看看:
https://blog.csdn.net/Gou_Hailong/article/details/113308630
如果想使用gpuArray的话,需安装支持它的相应matlab版本。
有关GPU的知识,笔者了解还尚浅,暂不能做详细的笔记
二、代码
1、语法
yy = smooth(y)
yy = smooth(y,span)
yy = smooth(y,method)
yy = smooth(y,span,method)
yy = smooth(y,'sgolay',degree)
yy = smooth(y,span,'sgolay',degree)
yy = smooth(x,y,___)
gpuarrayYY = smooth(gpuarrayY,___)
gpuarrayYY = smooth(gpuarrayX,gpuarrayY,___)
- yy = smooth(y) 滑动平均,窗口为5,得到的结果是一个列向量。
- yy = smooth(y,span) span 控制窗口大小
- yy = smooth(y,method) 指定平滑算法,平滑算法有好多种,下面有简介。
- yy = smooth(y,span,method) 指定窗口大小+平滑算法
- yy = smooth(y,‘sgolay’,degree) 指定多项式平滑算法+多项式次数,次数要小于窗口大小,因为确定一个n次多项式,需要n+1个值,至少需要n+1组数据。
- yy = smooth(y,span,‘sgolay’,degree) 指定窗口大小+多项式平滑算法+多项式次数
- yy = smooth(x,y,___) 多一个自变量x,x的含义见于下面,横线表示选项可取上面任意一种。
- gpuarrayYY = smooth(gpuarrayX,gpuarrayY,___) 于上边的类似,只是使用的数据为gpuArray类型的数据而已,其他于上面相同。
- span的取值可以是整数或是(0,1)范围内的小数,代表所有数据的百分比,0.1代表10%
- x为响应数据y的自变量,指定为列向量。 如果不提供x,则要求x的方法假定x = 1:length(y)。 当y未排序或均匀分布时,请指定x数据。 如果x不均匀且未指定方法,则使用lowess。如果指定要求对x进行排序的平滑方法,则该函数会自动对x数据进行排序。
- 仅当使用默认方法“滑动平均”时,才建议将gpuArray x和y输入与平滑函数一起使用。 将GPU数据与其他方法一起使用不会提供任何性能优势。
2、Method
| Method | 描述 |
|---|---|
| moving(默认) | 滑动平均平滑,滤波系数等于窗口大小的倒数 |
| lowess | 局部加权线性回归平滑,使用加权线性最小二乘法和一级多项式模型进行局部回归 |
| loess | 局部加权二次回归平滑,使用加权线性最小二乘法和二次多项式模型进行局部回归 |
| sgolay | 多项式平滑,Savitzky-Golay滤波器。 广义移动平均,其滤波器系数由未加权的线性最小二乘回归和指定度数的多项式模型确定(默认值为2)。 该方法可以接受不一致的预测变量数据。 |
| rlowess | 鲁棒局部加权线性回归平滑,“ lowess”的加强版,可为回归中的异常值分配较低的权重。 该方法将零权重分配给六个均值绝对偏差之外的数据。 |
| rloess | 鲁棒局部加权二次回归平滑,“loess”的加强版,在回归中将较低的权重分配给离群值。 该方法将零权重分配给六个均值绝对偏差之外的数据。 |
3、例子
x = (0:0.1:15)';
y = sin(x) + 0.5*(rand(size(x))-0.5);
y([90,110]) = 3;
yy1 = smooth(x,y,0.1,'loess');
yy2 = smooth(x,y,0.1,'rloess');
subplot(2,1,1)
plot(x,y,'b.',x,yy1,'r-')
set(gca,'YLim',[-1.5 3.5])
legend('Original data','Smoothed data using ''loess''',...
'Location','NW')
subplot(2,1,2)
plot(x,y,'b.',x,yy2,'r-')
set(gca,'YLim',[-1.5 3.5])
legend('Original data','Smoothed data using ''rloess''',...
'Location','NW')
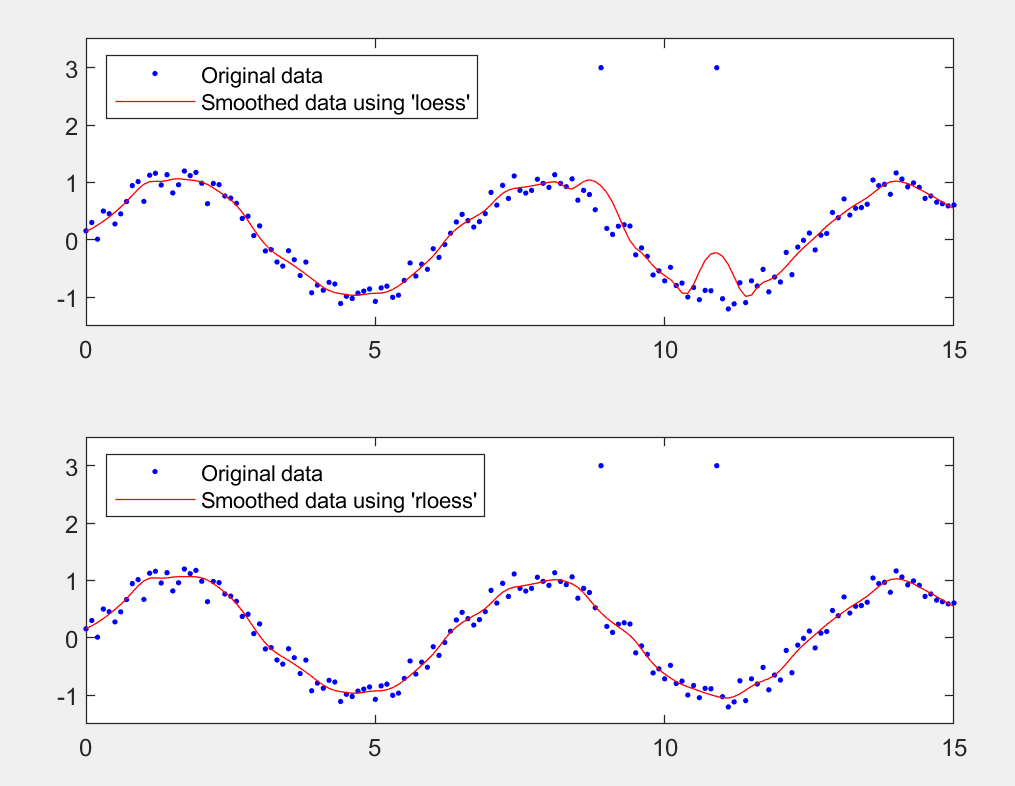
可以看出rloess效果要好一些,一般情况下,可以无脑使用:
b=smooth(a,'rloess');
b=smooth(a,'rlowess');
三、自编函数
matlab自带的平滑算法会改变原始数据,但是有时候笔者只想将一组数据中的离群数给剔除,不改变其他原始数据,所以笔者编写了个函数,如下所示:
1、V1.0
不考虑前后向量长度的话,一句话就搞定:
c=b(abs(b-mean(b))<= 3*std(b));
2、V2.0
要保持前后向量长度不变的话:
% rm data which > 3*std once
function data=rmNo(mat)
m=nanmean(mat);
s=std(mat);
dat=smooth(mat,'rlowess');
ind=find(abs(mat-m)>3*s);
data=mat;
for i=ind
data(i)=dat(i);
end
end
3、V3.0
比如现在我有一组数据,经历过一次消噪,噪声水平设置标准为大于3倍标准差。消噪之后的数据标准差发生了变化,所以之前有可能不是噪点的数据也会变成噪点。我想把这些噪点给消了,那么就需要一个迭代过程:
% rm data which > 3*std iterate
function data=rmNo1(mat)
count=0;
mat0=mat;
mat1=mat0;
while true
m=nanmean(mat0);
s=std(mat0);
dat=smooth(mat0,'rlowess');
ind=find(abs(mat0-m)>3*s);
for i=ind
mat1(i)=dat(i);
end
count=count+1;mat0=mat1;
if count>5 || length(ind)==0
break;
end
end
data=mat1;
end
迭代终止条件为:迭代超过5次或前后两次迭代结果相同。
最后
以上就是现代信封最近收集整理的关于Matlab Smooth函数/丝滑数据一、预备知识二、代码三、自编函数的全部内容,更多相关Matlab内容请搜索靠谱客的其他文章。








发表评论 取消回复