MATLAB画系统函数H(z)零极点以及幅频特性

问题引入

绘制出下式系统函数H(z)的单位冲激响应和频响曲线
$$H(z)=\frac{z-0.5}{z}$$

问题解决

1. 数学变换

原式可化为
$$H(z)=\frac{z-0.5}{z}=1-0.5z^{-1}$$
将上式进行z逆变换可以得到
$$h(n)=\delta (n)-0.5\delta (n-1)$$
按照上式使用MATLAB画图

clear;close all;clc;
step = 1;
tt=0:1:60;
hh=zeros(1,length(tt));
hh(1)=1;
hh(1/1+1)=-0.5;
figure;
plot(tt, hh) 
title("h(t)");
xlabel("N");ylabel("h(t)");

画图结果：

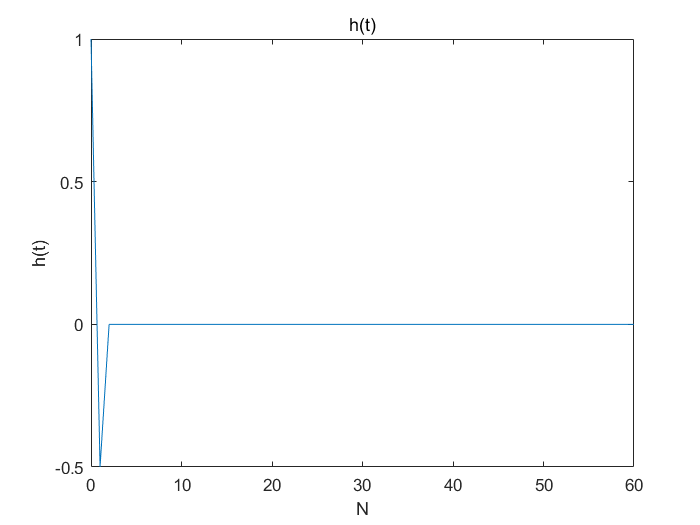
从原式可看出
零点为 z = 0.5 ; 极点为z = 0

2. 直接画图

原式
$$H(z)=\frac{z-0.5}{z}$$
对于分子b：
一次项系数为1 ，零次项系数为-0.5
因此b=[1 -0.5]
对于分子a：
一次项系数为1 ，零次项系数为0
因此a=[1 0]
使用impz函数画单位冲激响应，使用freqz函数画幅频特性曲线，使用zplane函数画零点极点图

MATLAB代码如下

clear;close all;clc;
B=[1,-0.5];
A=[1 0];
N=60;
[h,t]=impz(B,A,N);
figure;plot(t,h)
title("h(t)");
xlabel("N");ylabel("h(t)");
figure;
freqz(B,A);
figure;
zplane(B, A) 

单位冲激响应：

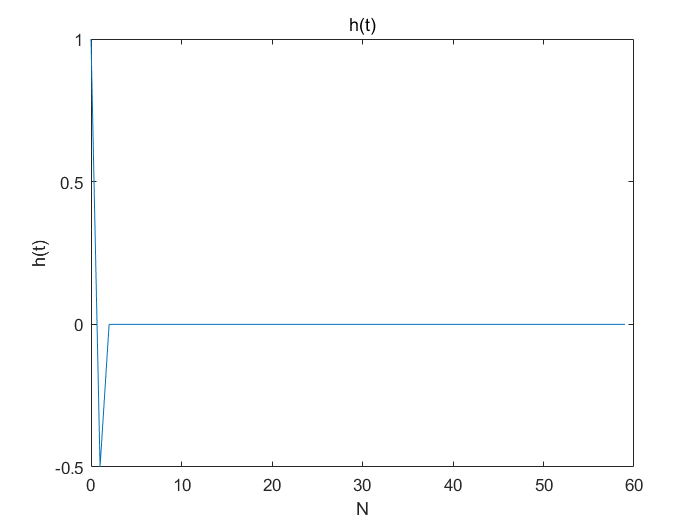
幅频响应：

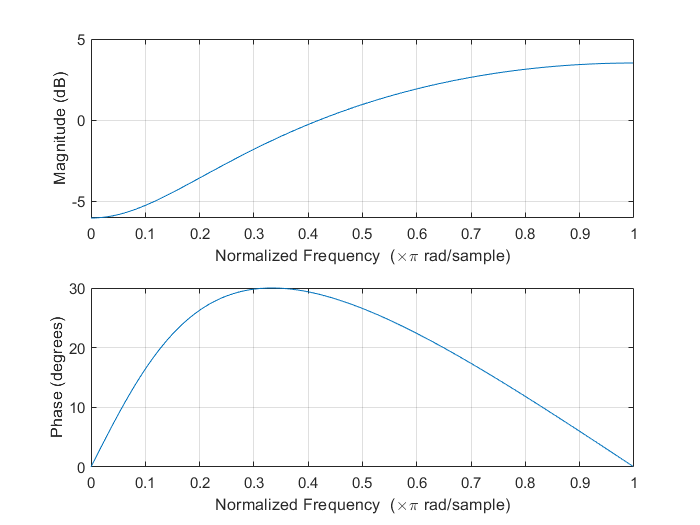
极点图：

最后

以上就是鳗鱼小丸子为你收集整理的MATLAB画系统函数H(z)零极点以及幅频特性的全部内容，希望文章能够帮你解决MATLAB画系统函数H(z)零极点以及幅频特性所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。