线性系统频域校正-校正必读

【自控笔记】5.7线性系统频域校正

一、三频段划分

为了更方便地研究对数幅频特性与系统性能指标的关系，通常将$L(\omega )$人为地分成三个频段：低频段、中频段和高频段，如下图所示：

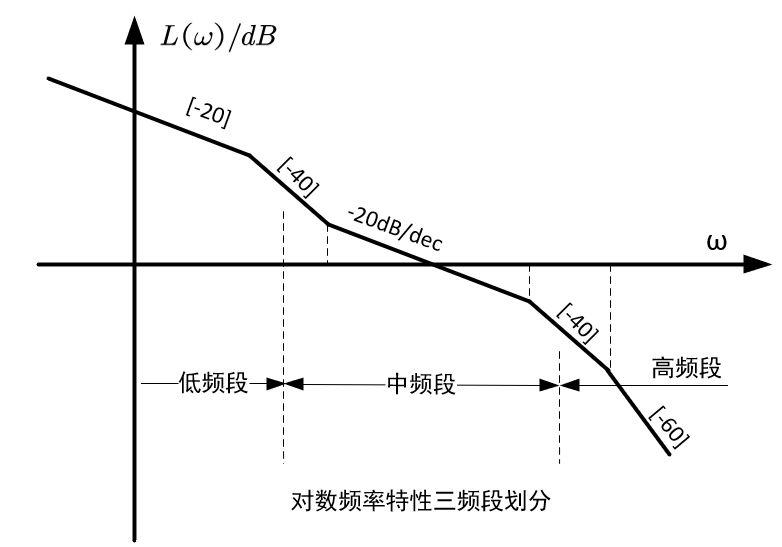
低频段主要是指第一个转折频率以左的频段。这一频段的特性完全是由积分环节和开环增益决定，其对应的传递函数为$\frac{K}{s^v}$。

中频段是指截止频率${\omega }_c$附近的频段。这一频段集中反映了闭环系统动态响应的平稳性和快速性，一般希望对数幅频特性曲线以-20dB/dec的斜率穿过0dB线，这样的系统就获得较长的带宽，从而相角裕度较大，系统超调量较小，系统性能越好。

高频段是指频率远大于截止频率${\omega }_c$的频段。高频段特性是由小时间常数环节构成的，斜率越陡，幅值衰减得越快，系统抗高频干扰性能越好。

三频段理论为系统的校正提供了原则和方向。熟练掌握校正装置各个转折频率之间的倍频比，是解决校正问题的关键所在。

二、串联超前校正

串联超前校正，实质上就是利用超前网络相角超前特性提高系统的相角裕度。

无源超前网络的电路图如下所示：

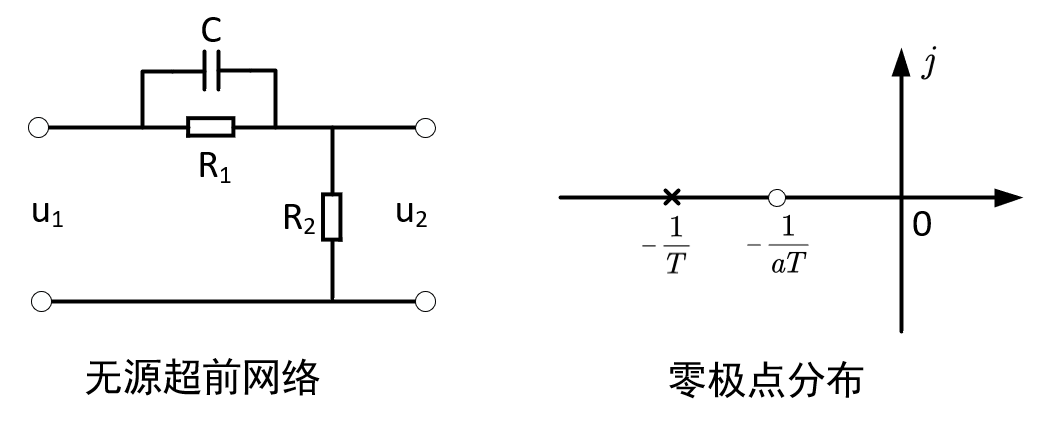
根据电路图写出超前校正装置的传递函数可得：
$$G(s{)}_c=a{G}_c^{{}^{\prime }}(s)=\frac{aTs+1}{Ts+1}$$
其中$a=\frac{R_1+R_2}{R_2}>1$，$T=\frac{R_1{R}_{2}C}{R_1+R_2}$。于是就确定了超前网络的零极点关系，转折频率亦容易得知，它的对数频率特性曲线如下：

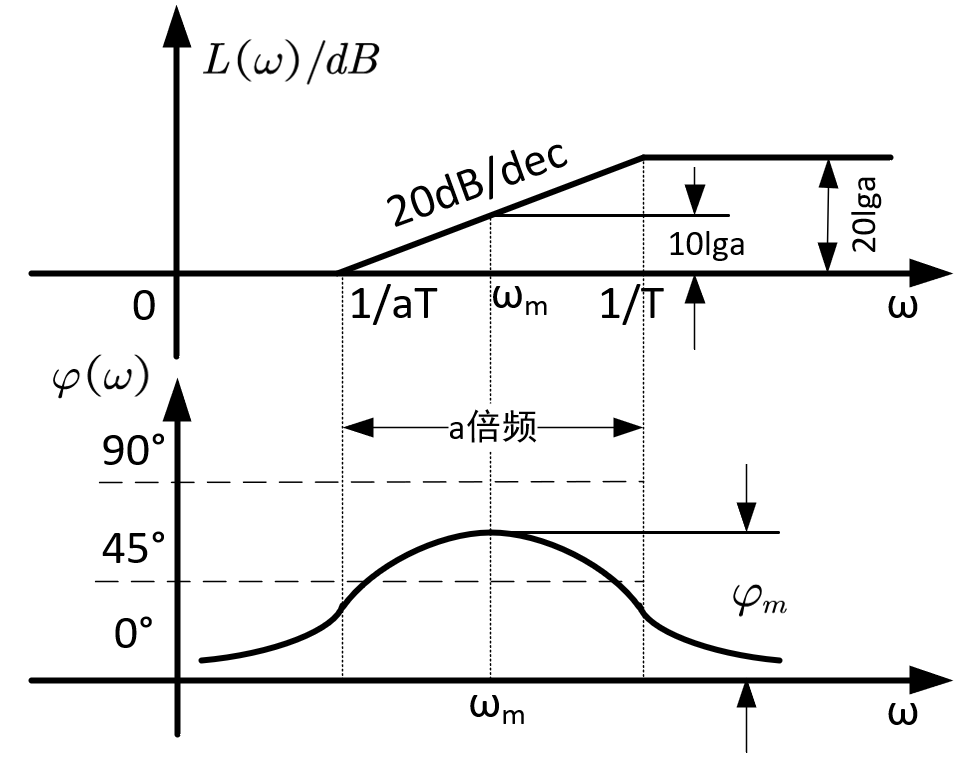
观察它的对数频率特性，超前网络最大能使原系统的幅值抬高20lga dB，且该高度只和转折频率有关。超前网络最大的相角${\phi }_m$在两个转折频率的中点处，超前校正就是将这一点处的频率特性补到原系统中，使系统的相角提升${\phi }_m$（实际上补不到${\phi }_m$，因为校正后的系统由于截止频率后移，相角还会衰减几度。），幅值提升10lga。

那么，最大该超前网络的${\phi }_m$最大能有多少呢？

由$G(s{)}_c$表达式可以知道它的相角为:
$${\phi }_c(\omega )=arctanaT\omega -arctanT\omega$$
对${\phi }_c(\omega )$求导并令其为0，可以算得${\phi }_m=arcsin\frac{a-1}{a+1}$，利用matlab绘制${\phi }_m$与a的关系曲线（代码附文末），如下图：

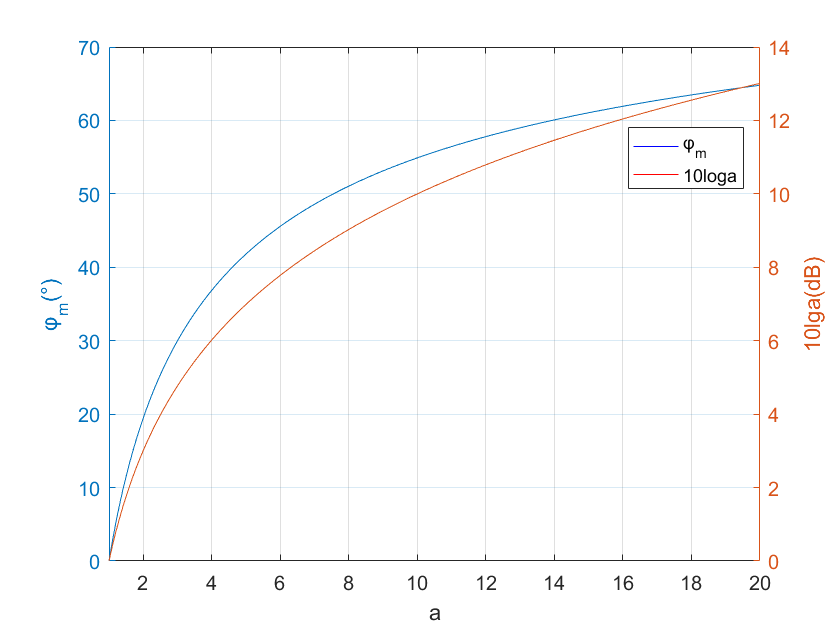
通过这个关系图，就能够看出$a\in (4,10)$范围内的超前校正最有效，既能高效抬高系统的相角裕度$\gamma$，又使得幅值增加不至于过大；而当a=14时，${\phi }_m=60°$，故一般认为一阶超前网络的最大超前角为60°。

三、串联滞后校正

串联滞后校正，实质上就是利用滞后网络幅值衰减特性挖掘系统自身的相角储备。也就是找到系统中满足相角要求的频率，并在该频率处使用滞后校正，使得系统幅值衰减，以该频率穿越0dB线。

无源滞后网络的电路图如下所示：

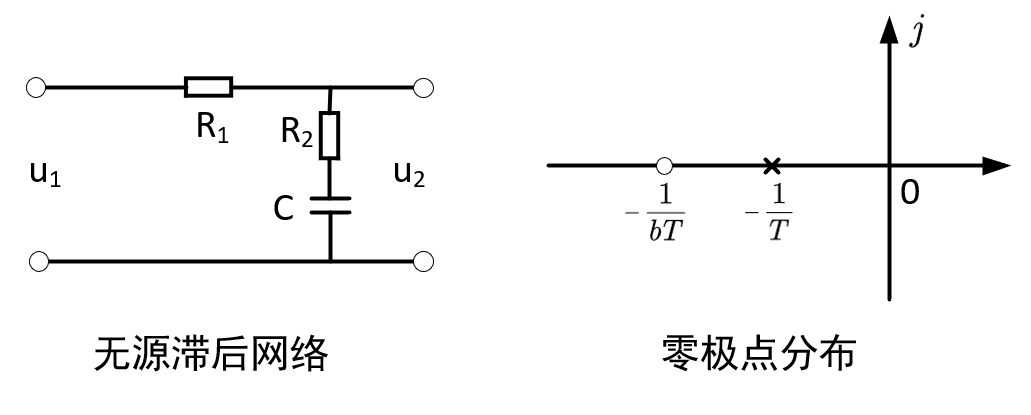
同样可以根据电路图得出滞后校正装置的传递函数：
$$G(s{)}_c=\frac{bTs+1}{Ts+1}$$
其中$b=\frac{R_2}{R_1+R_2}<1$，$T=(R_1+R_2)C$

于是滞后网络的零极点关系和转折频率都容易获得，它的对数频率特性曲线如下：

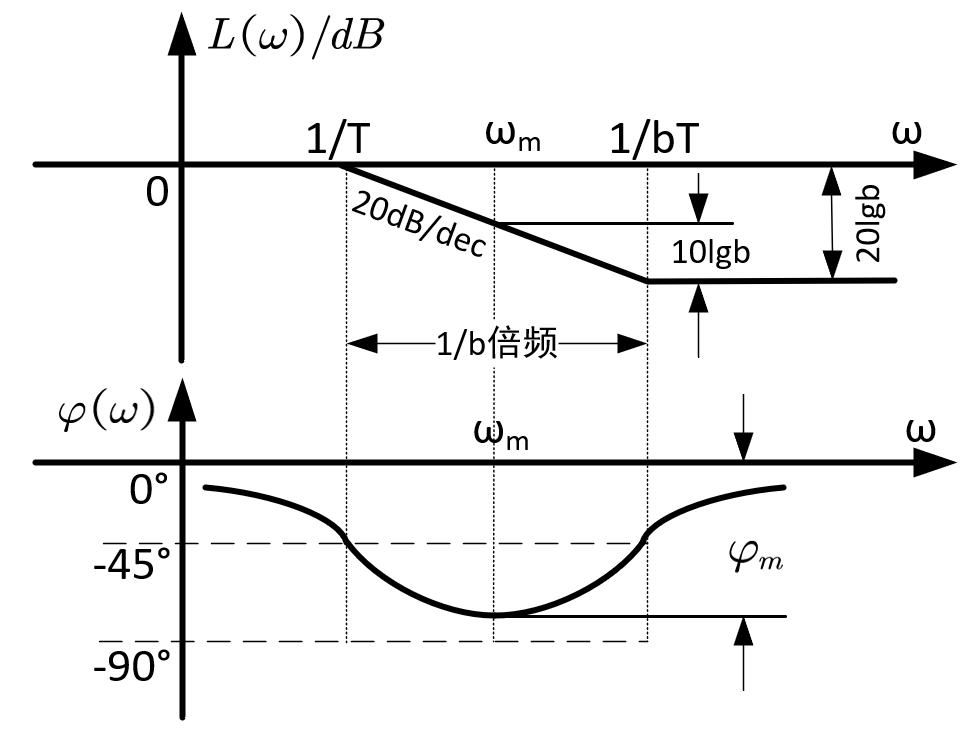
一般来讲，相角裕度越大，系统越稳定，所以使用滞后校正装置时既希望它能使系统幅值衰减，又要避免相角裕度的损失。观察它的对数幅频特性曲线，可以知道在1/bT处之后的频率特性幅值得到最大程度的衰减，而相角损失也不大。在实际使用过程中，常常选取10b/T处的频率特性进行校正，也就是滞后校正装置第二个转折频率往后十倍频处。

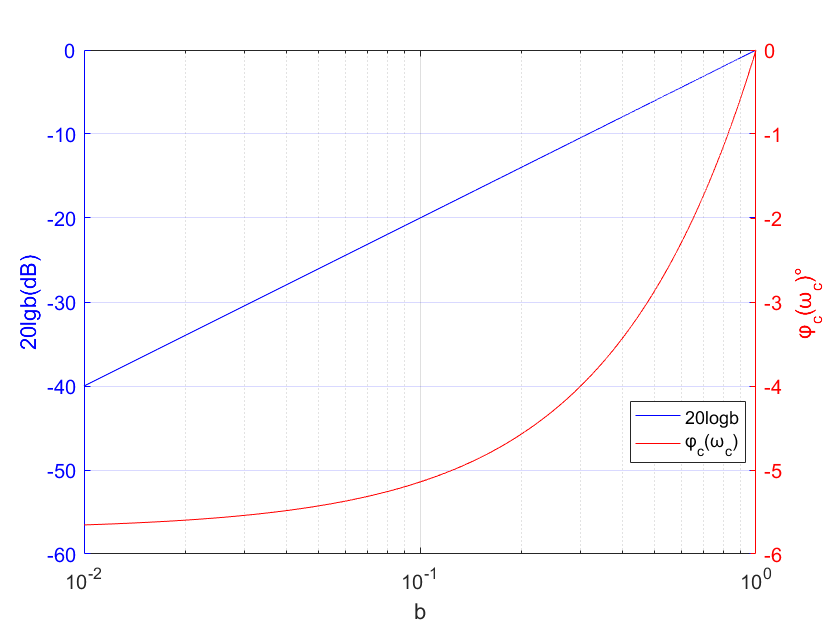
同样的，使用matlab绘制频率为$\frac{10}{bT}$处的相角衰减（代码附文末），可以看出，相角损失最大不超过-6°。在使用滞后装置进行校正时，应该要考虑到该相角损失。

四、串联滞后-超前校正

串联滞后-超前校正，实质上就是综合利用滞后网络幅值衰减、超前网络相角超前的特性，改造开环频率特性，提高系统性能。

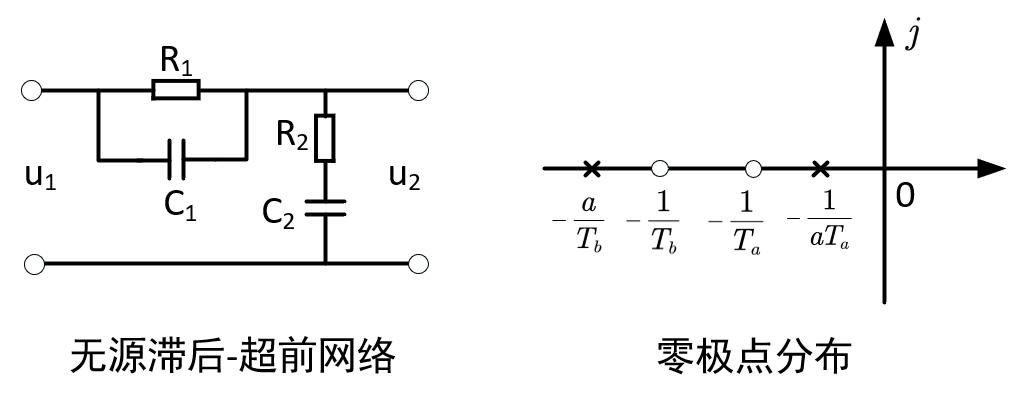
根据电路图，可以的得到滞后-超前校正网络的传递函数
$$G(s{)}_c=\frac{(R_1{C}_{1}s+1)(R_2{C}_{2}s+1)}{R_1{C}_1{R}_2{C}_2{s}^2+(R_1{C}_1+R_2{C}_2+R_1{C}_2)s+1}$$

$$G(s{)}_c=\frac{(T_{a}s+1)(T_{b}s+1)}{T_a{T}_b{s}^2+(T_a+T_b+T_{ab})s+1}$$

令$a{T}_a+\frac{T_b}{a}=T_a+T_b+T_{ab}$可得
$$G(s{)}_c=\frac{(T_{a}s+1)}{(a{T}_{a}s+1)}\cdot \frac{(T_{b}s+1)}{\frac{T_b}{a}s+1}$$

又因为$a>1，T_a/T_b=a^2$，所以各环节系数大小关系为
$$a{T}_a>T_a>T_b>T_b/a$$

由此便可以得到转折频率以及零极点关系，滞后-超前的对数频率特性如下所示：

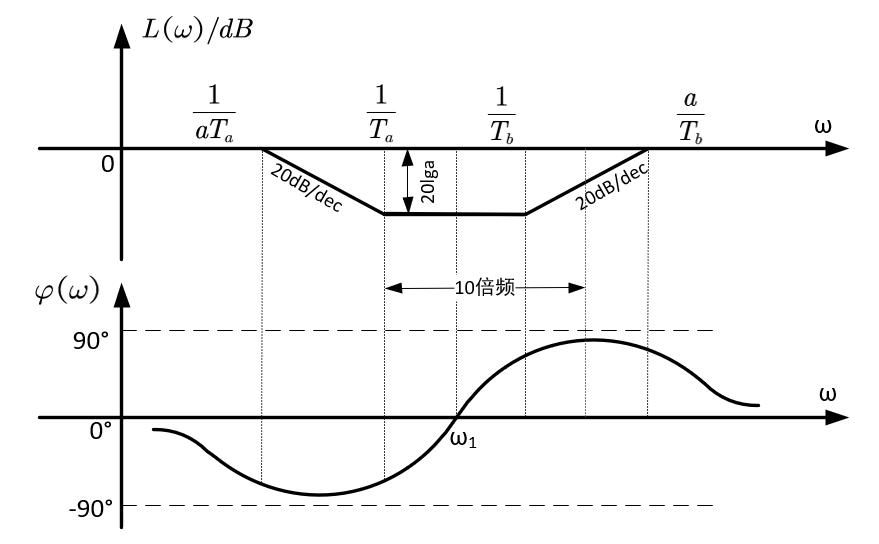
为了综合利用滞后超前网络幅值衰减，相角超前的特性，将校正后系统的截止频率选在$1/T_b$与$a/T_b$处，此处所获得的相角为最大值${\phi }_m$，幅值衰减10lga。

附录

${\phi }_m$与a的关系曲线绘制matlab代码：

clear;clc  

a=1:0.1:20;
for i = 1 :length(a)
    phim(i)=asin((a(i)-1)/(a(i)+1))*180/pi;
    L(i)=10*log10(a(i));
end

h=plotyy(a,phim,a,L);
grid on;
xlabel('a')
ylabel(h(1),'{φ_m}(°)')
ylabel(h(2),'10lga(dB)')
set(h(1),'xlim',[1,20])
set(h(2),'xlim',[1,20])
set(h(1),'ylim',[0,70])
set(h(2),'ylim',[0,14])
legend('{φ_m}','10loga');

滞后网络关系曲线绘制matlab代码：

clear;clc;close all

b=0.01:0.0001:1.0;
for i = 1 :length(b)
    Lgb(i)=20*log10(b(i));
    phiw(i)=atan(0.1*(b(i)-1))*180/pi;
end

figure(1)
h1=axes('position',[0.1,0.12,0.8,0.8]);
semilogx(b,Lgb,'b-'); grid on
hold on
semilogx(b,phiw*10,'r-');
legend('10logb','{φ_c(ω_c)}');
set(h1, 'yaxislocation', 'left')
xlabel('b');
ylabel('20lgb(dB)');

h2 = axes('position', [0.899 0.12 0.001 0.8]); 
set(h2, 'ycolor', 'r');
set(h2, 'yaxislocation', 'right', 'xtick', []);
ylabel('{φ_c(ω_c)°}');
set(h2,'ylim',[-6,0]);

最后

以上就是发嗲小蘑菇为你收集整理的线性系统频域校正-校正必读的全部内容，希望文章能够帮你解决线性系统频域校正-校正必读所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。