目录
一、理论基础
二、核心程序
三、仿真测试结果
一、理论基础
两层基站（BS）组成整个通讯网络，第 1 层为 Macro 基站记为fai1 ，第 2 层为 Micro 基站记为 fai2 ，均服从泊松分布，相互独立，密度分别为 。 根据 fai1， fai2 （这里取值根据画图美观程度而定，不一定要和后面的计算相同）的密度在 坐标为 10×10km 的面积内、按照泊松分布随机生成若干个点（随机抛洒两遍 nodes，两层 叠加起来），然后画成 voronoi 图。也就是在相邻两个点（同种类的点）之间距离的二分之 一处画一条线。
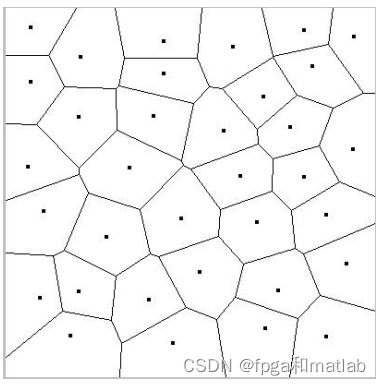
Voronoi图，又叫泰森多边形或Dirichlet图，它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。Voronoi图，又叫泰森多边形或Dirichlet图，它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。N个在平面上有区别的点，按照最邻近原则划分平面；每个点与它的最近邻区域相关联。Delaunay三角形是由与相邻Voronoi多边形共享一条边的相关点连接而成的三角形。Delaunay三角形的外接圆圆心是与三角形相关的Voronoi多边形的一个顶点。
Voronoi图是Delaunay三角剖分的对偶图，生成它的方法有很多，比较有名的有分治算法，扫描线算法，增量法等。但利用Delaunay三角剖分生成Voronoi图的算法是最快的。但最快的方法则是构造Delaunay三角剖分，再连接相邻三角形的外接圆圆心，即可以到Voronoi图。
Delaunay三角剖分算法：
对于给定的初始点集P，有多种三角网剖分方式，其中Delaunay三角网具有以下特征：
1、Delaunay三角网是唯一的；
2、三角网的外边界构成了点集P的凸多边形“外壳”；
3、没有任何点在三角形的外接圆内部，反之，如果一个三角网满足此条件，那么它就是Delaunay三角网。
4、如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大，从这个意义上讲，Delaunay三角网是“最接近于规则化的“的三角网。
Delaunay三角形网的特征又可以表达为以下特性：
1、在Delaunay三角形网中任一三角形的外接圆范围内不会有其它点存在并与其通视，即空圆特性；
2、在构网时，总是选择最邻近的点形成三角形并且不与约束线段相交；
3、形成的三角形网总是具有最优的形状特征，任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话，那么两个三角形6个内角中最小的角度不会变大；
4、不论从区域何处开始构网，最终都将得到一致的结果，即构网具有唯一性。
用户也服从泊松随机分布，在指定区域内选择一个基站进行通讯连接。 用户（user）选择与某个基站 j 建立连接遵循如下规则：
首先计算随机选择的一个典型用户与周围基站的距离，再按照{ ，k=1,2} 规则把距离代入，计算出结果，选择最大值与之连接。
定义参数：
Pt1 ，Pt2 分别为 macro 和 micro 的传输功率
X1 为 user 到 BS1 之间的距离
X2 为 user 到 BS2 之间的距离
最后更加如下规则计算SINR：
二、核心程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214clc; clear; close all; warning off; addpath 'func' %B2的取值范围 B2set = [0.25:0.25:5]; lemdas = [0.25:0.25:5]*1e-5; for bj = 1:length(B2set) B2set(bj) for lj = 1:length(lemdas) %产生网络图 %User个数 Nu = 50; Lemdau = 90; %蒙特卡洛循环次数 MTKL = 10000; %选择一个典型的用户 UserID = 15; %随便设置一个 for mt = 1:MTKL RandStream.setDefaultStream(RandStream('mt19937ar','seed',mt)); L = 10e3; N1 = 30; N2 = 40; Lemda1 = 5e-5; Lemda2 = lemdas(lj); %Macro层1的相关参数 %泊松分布 x1 = poissrnd(Lemda1*1e7,[1,N1]);x1=L*x1/max(x1); y1 = poissrnd(Lemda1*1e7,[1,N1]);y1=L*y1/max(y1); %Micro层2的相关参数 %泊松分布 x2 = poissrnd(Lemda2*1e7,[1,N2]);x2=L*x2/max(x2); y2 = poissrnd(Lemda2*1e7,[1,N2]);y2=L*y2/max(y2); %产生符合泊松随机分布的用户的区域位置 xu = poissrnd(Lemdau,[1,Nu]);xu=L*xu/max(xu); yu = poissrnd(Lemdau,[1,Nu]);yu=L*yu/max(yu); %参数的设定 epsl = 1e6;%数据包量 alpha1 = 4; alpha2 = 3.6; delta2 = -106; B = 1e3; Pt1 = 40; Pt2 = 5; h = 1; DeltaB1= 1; %************************************************************************** %DeltaB2待求 DeltaB2= B2set(bj); %计算每个用户的信号的强度 for i = 1:Nu %针对Macro %选择最近的一个基站，计算对应的距离 for j1 = 1:N1 dist_tmp1(j1) = sqrt((xu(i)-x1(j1))^2 + (yu(i)-y1(j1))^2); end dist1 = min(dist_tmp1); P1(i) = Pt1*h*DeltaB1*dist1^(-alpha1); %针对Micro %选择最近的一个基站，计算对应的距离 for j2 = 1:N2 dist_tmp2(j2) = sqrt((xu(i)-x2(j2))^2 + (yu(i)-y2(j2))^2); end dist2 = min(dist_tmp2); P2(i) = Pt2*h*DeltaB2*dist2^(-alpha2); %选择较大的一个联结 [V,I] = max([P1(i),P2(i)]); J(i) = I; end %计算得到的J为每个用户对应选择的基站标号 J; %根据如下规则计算SINR %定义与 Macro层BS连接的用户集合 U1 = find(J==1); %定义与 Micro层BS连接的用户集合 U2 = find(J==2); %计算SINR1和RATE1 %计算SINR2和RATE2 SINR1 = zeros(1,Nu); SINR2 = zeros(1,Nu); RATE1 = zeros(1,Nu); RATE2 = zeros(1,Nu); DeltaT1 = zeros(1,Nu); DeltaT2 = zeros(1,Nu); for i = 1:Nu %计算SINR1和RATE1 if J(i) == 1 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% for j1 = 1:N1 dist_tmp1(j1) = sqrt((xu(i)-x1(j1))^2 + (yu(i)-y1(j1))^2); end for j2 = 1:N2 dist_tmp2(j2) = sqrt((xu(i)-x2(j2))^2 + (yu(i)-y2(j2))^2); end [V1,I1]= min(dist_tmp1); dist1 = V1; FZ = Pt1*h*dist1^(-alpha1); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% ind1 = 0; tmps = []; for j1 = 1:N1 if (j1 < I1) | (j1 >I1) ind1 = ind1 + 1; tmps(ind1) = Pt1*h*dist_tmp1(j1)^(-alpha1); end end FM1 = sum(tmps); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% tmps = []; for j1 = 1:N2 tmps(j1) = Pt2*h*dist_tmp2(j1)^(-alpha2); end FM2 = sum(tmps); SINR1(i) = FZ/(FM1+FM2+10^(delta2/20)/1000); RATE1(i) = B*log2(1+SINR1(i)); DeltaT1(i) = epsl/RATE1(i); else SINR1(i) = 0; RATE1(i) = 0; DeltaT1(i) = 0; end %计算SINR2和RATE2 if J(i) == 2 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% for j1 = 1:N1 dist_tmp1(j1) = sqrt((xu(i)-x1(j1))^2 + (yu(i)-y1(j1))^2); end for j2 = 1:N2 dist_tmp2(j2) = sqrt((xu(i)-x2(j2))^2 + (yu(i)-y2(j2))^2); end [V2,I2]= min(dist_tmp2); dist2 = V2; FZ = Pt2*DeltaB2*h*dist2^(-alpha2); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% tmps = []; for j1 = 1:N1 tmps(j1) = Pt1*h*dist_tmp1(j1)^(-alpha1); end FM1 = sum(tmps); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% tmps = []; ind2 = 0; for j1 = 1:N2 if (j1 < I2) | (j1 >I2) ind2 = ind2 + 1; tmps(ind2) = Pt2*h*dist_tmp2(j1)^(-alpha2); end end FM2 = sum(tmps); SINR2(i) = FZ/(FM1+FM2+10^(delta2/20)/1000); RATE2(i) = B*log2(1+SINR2(i)); DeltaT2(i) = epsl/RATE2(i); else SINR2(i) = 0; RATE2(i) = 0; DeltaT2(i) = 0; end end %计算E Pbs1 = zeros(1,Nu); Pm1 = zeros(1,Nu); Pbs2 = zeros(1,Nu); Pm2 = zeros(1,Nu); for i = 1:Nu if J(i) == 1 Pbs1(i) = alpha1*Pt1; else Pbs1(i) = 0; end if J(i) == 2 Pbs2(i) = alpha2*Pt2; else Pbs2(i) = 0; end E(i) = DeltaT1(i)*Pbs1(i) + DeltaT2(i)*Pbs2(i); end E2(mt) = E(UserID); end E3(lj,bj) = mean(E2); end end [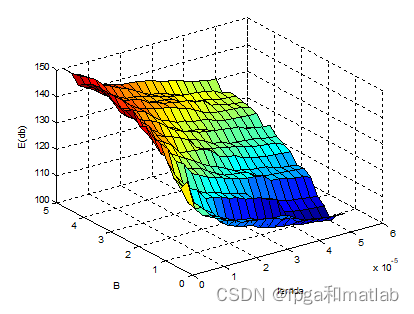X,Y] = meshgrid(lemdas,B2set); figure surf(X,Y,20*log10(E3')); xlabel('lemda'); ylabel('B'); zlabel('E(db)');
三、仿真测试结果
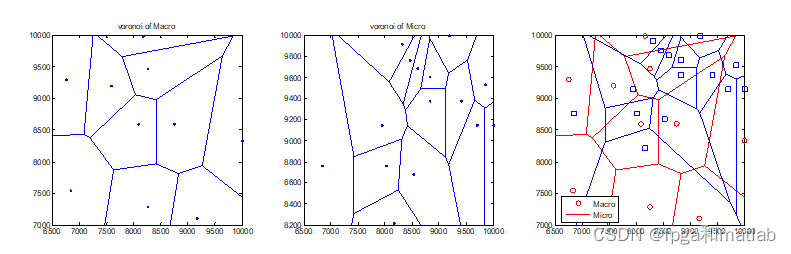
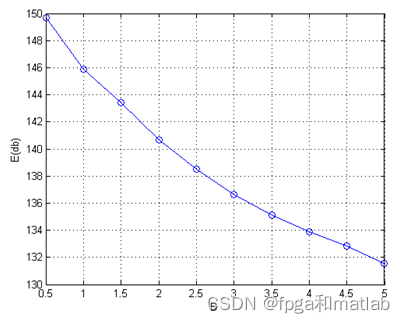
仿真效果如下所示：
A12-11
最后
以上就是无奈大门最近收集整理的关于基于用户泊松随机分布通讯网络的voronoi图的matlab仿真一、理论基础二、核心程序三、仿真测试结果的全部内容，更多相关基于用户泊松随机分布通讯网络内容请搜索靠谱客的其他文章。
发表评论 取消回复