23.2.8每日总结

96 阅读 0 评论 64 点赞

我是靠谱客的博主拼搏白羊，最近开发中收集的这篇文章主要介绍23.2.8每日总结，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

今天学习了背包问题，先从01背包问题开始说起吧，01背包问题就是有n件物品，一个容量为v的背包。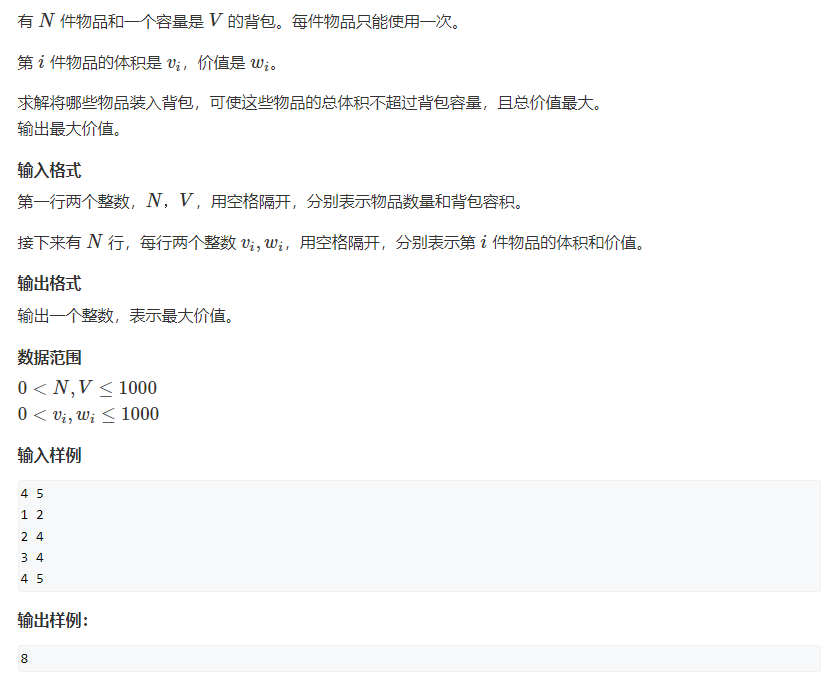

01背包问题作为背包问题中的基础问题，我们解决这类问题的时候最重要的就是求出相对应的状态转移方程，那么如何找出状态转移方程呢，我们可以进行打表的方式来解决这个问题，就是画一个二维数组，然后有i行j列，然后将每个物品的价值和体积放在前面，然后写出每一个情况下该背包的最大价值写在表格中，然后就可以推出它的状态转移方程了就比如这个题的状态转移方程就是d【i】【j】=max（d【i-1】【j】，d【i-1】【j-w【i】】+c【i】）

然后用用二维数组写的话代码如下

#include<bits/stdc++.h>
using namespace std；
int v[1005];   
int w[1005];    
int f[100][100];  

int main() 
{
    int n, m;   
    cin >> n >> m;
    for(int i = 1; i <= n; i++) 
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++) 
        for(int j = 1; j <= m; j++)
        {
            if(j < v[i]) 
                f[i][j] = f[i - 1][j];
            else    
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }           

    cout << f[n][m] << endl;
    return 0;
}

其实是可以在这个基础上进行优化，优化的话就是要从j=m开始进行然后状态转移3方程是就变为

dp【j】=max（d【j】，d【j-w【i】】+c【i】

因为01背包问题的每个数据都是根据上面一行的数据推出来的且是由前推后，所以说j要从m开始

#include<bits/stdc++.h>
using namespace std;
int f[1005];  

int main() 
{
    int n, m;   
    cin >> n >> m;

    for(int i = 1; i <= n; i++) {
        int v, w;
        cin >> v >> w;      
        for(int j = m; j >= v; j--)
            f[j] = max(f[j], f[j - v] + w);
    }

    cout << f[m] << endl;

    return 0;
}

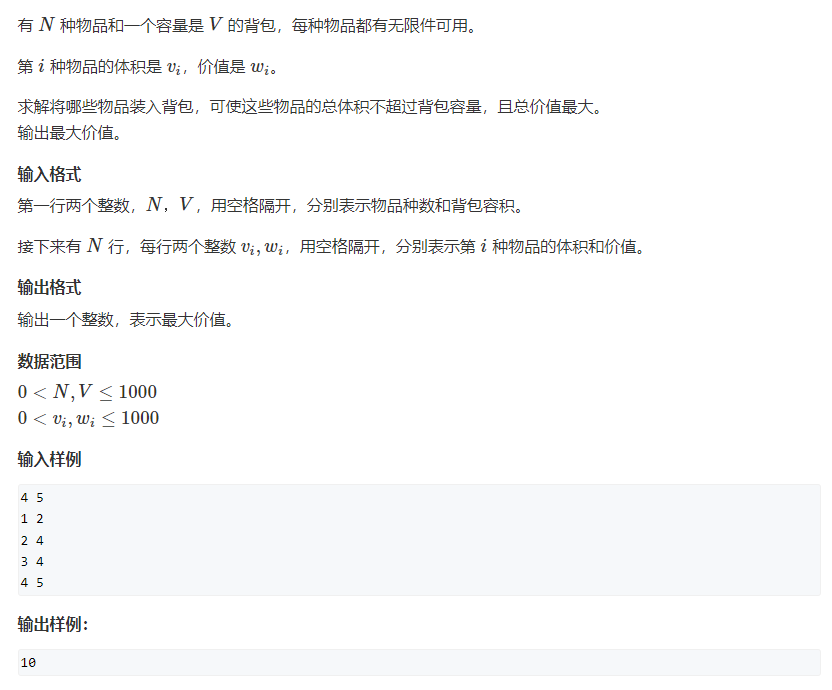
接下来就开始解决完全背包问题，这个问题与01背包问题不同的是每个物品都有无限件可以使用所以说我们就需要要在其代码上进行一些改变朴素的方法就是在上面的二维那个解决方法下在j的for循环里面再添加一个for（int k=0；k+v【i】<=j；k++）就好了然后将其状态转移方程式改写一下就好了

#include<iostream>
using namespace std;
int n, m;
int dp[100][100], v[100], w[100];

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ )
        cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i ++ )
        for(int j = 0; j <= m; j ++ )
            for(int k = 0; k * v[i] <= j;k++)
                dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]);
    cout << dp[n][m] << endl;
return 0;
}

这个其实也是可以优化的这个最后优化出来的状态转移方程式和01背包问题优化出来的方程式是一样的的，但是不同的是完全背包问题是根据同一行的数据推出来的所以里面的j需要从0开始，其实也可以直接从w【i】开始

#include<iostream>
using namespace std;
int f[100];
int v[100],w[100];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1 ; i <= n ;i ++)
    {
        cin>>v[i]>>w[i];
    }
    for(int i = 1 ; i<=n ;i++)
    for(int j = v[i] ; j<=m ;j++)
    {
            f[j] = max(f[j],f[j-v[i]]+w[i]);
    }
    cout<<f[m]<<endl;
return 0;
}