1 Counters

1.1 Four-bit binary counter

构建一个4位二进制计数器，其计数范围为0到15（含15），周期为16。重置输入是同步的，应将计数器重置为0。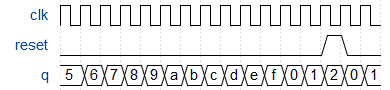

1.1.1 解决思路

该题可以从同步时序逻辑电路的设计方法入手，由于没有入参，因此只能构建Moore型FSM。

1.1.2 代码实现

下面给出实现代码。

• 方法一：使用D触发器实现

module dff_mod(
    input clk,
    input d,
    input reset,
    output reg q
);
    always @ (posedge clk)
        if(reset == 1)
            q <= 0;
        else
            q <= d;
endmodule

module top_module (
    input clk,
    input reset,      // Synchronous active-high reset
    output [3:0] q);

    wire [3:0] d;
    
    assign d[0] = ~q[0];
    assign d[1] = q[0] ^ q[1];
    assign d[2] = ~q[1] & q[2] | ~q[0] & q[2] | q[0] & q[1] & ~q[2];
    assign d[3] = ~q[2] & q[3] | ~q[1] & q[3] | ~q[0] & q[3] | q[0] & q[1] & q[2] & ~q[3];
    
    genvar i;
    generate
        for(i = 0; i < 4; i =i +1) begin: dff_loop
            dff_mod dff0(clk, d[i], reset, q[i]);        
        end
    endgenerate
     
endmodule

• 方法二：使用加法器实现

module top_module (
    input clk,
    input reset,      // Synchronous active-high reset
    output [3:0] q);
    always @ (posedge clk)
        if(1 == reset)
            q <= 4'b0;
        else
            q <= q + 1'b1;
endmodule

1.2 Decade counter again

制作一个计数为1到10（含10）的十进制计数器。重置输入是同步的，应将计数器重置为1。

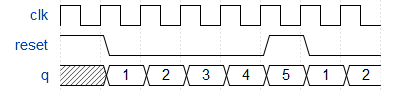
1.2.1 解题思路

因为本题的目的是设计计数器，没有输入来源，因此只能设计Moore型同步时序电路来实现题干要求。对应的状态转换如下图所示。

10个状态的转换，需要4个触发器来维护状态的切换。结合题目信息，从0001编号到1010共10个状态，与计数器输出值保持一致。基于原始状态转移图和状态编码信息，写出状态转移表。相应地，结合表格输出各个次态的卡诺图，并相应化简，得到逻辑方程组。检查自启动能力，给出逻辑图。
考虑该题的计数基准是从1开始的，并且复位归1而非归0，因[]此需要考虑D触发器的设计方式与常用的D触发器不同。

1.2.2 代码实现

• 方法一：使用触发器实现

module dff_fourbit(
    input clk,
    input reset,
    input [3:0] d,
    output reg [3:0] q);
    always @ (posedge clk)
        if (1 == reset)
            q <= 4'b0001;
        else
            q <= d;
endmodule


module top_module (
    input clk,
    input reset,
    output [3:0] q);
    
    wire [3:0] d;
    assign d[0] = ~q[0];
    assign d[1] = ~q[1] & q[0] | ~q[3] & q[1] & ~q[0];
    assign d[2] = q[2] & ~q[1] | q[2] & ~q[0] | ~q[2] & q[1] & q[0];
    assign d[3] = q[3] & ~q[1] | q[2] & q[1] & q[0];
    
    dff_fourbit dff0(.clk(clk), .reset(reset), .d(d), .q(q));
    
endmodule

• 方法二：使用加法器实现

module top_module (
    input clk,
    input reset,
    output [3:0] q);
    
    always @ (posedge clk)
        if(1 == reset)
            q <= 4'b1;
        else if(10 == q)
            q <= 4'b1;
        else
            q <= q + 1'b1; 
endmodule

1.3 Slow decade counter

构建一个从0到9（含）计数的十年计数器，周期为10。重置输入是同步的，应该将计数器重置为0。我们希望能够暂停计数器，而不是总是在每个时钟周期递增，因此slowena输入指示计数器何时递增。

1.3.1 解题思路

该题的核心是引入输入使能端控制计数器的增加，当输入不使能时，计数器保持不变，输入使能时，计数器正常累加。本题如果采用触发器来实现，可设计Mealy型或者Moore型状态机来实现。

1.3.2 代码实现

• 方法一：使用触发器实现
  使用状态机来完成10个状态的切换，并验证是否具备自校正能力。
• 画出状态转换图、并输出逻辑方程组，写出相应实现代码。
• 方法二：使用加法器实现

    input clk,
    input slowena,
    input reset,
    output [3:0] q);
    
    always @ (posedge clk)
        if(1 == reset)
            q <= 4'b0;
    	else if(1 == slowena) begin
            if(9 == q)
                q <= 4'b0;
            else
                q <= q + 1'b1;
    	end
endmodule

1.4 Counter 1-12

设计具有以下输入和输出的1-12计数器：

• Reset同步激活高电平复位，强制计数器为1；
• Enable启用高电平以运行计数器；
• Clk上升边缘触发时钟输；
• Q[3:0]表示计数器的输出；
• c_enable、c_load、c_d[3:0]控制信号发送至提供的4位计数器，因此可以验证正确的操作。
  你可以使用以下组件：
• 下面的4位二进制计数器（count4），具有enable和同步并行load输入（load优先级高于enable）。count4模块已提供给你。在电路中实例化它。
• 逻辑门

module count4(
	input clk,
	input enable,
	input load,
	input [3:0] d,
	output reg [3:0] Q
);

c_load、c_enable和c_d输出分别是发送到内部计数器的enable、load和d输入的信号。其目的是检查这些信号的正确性。

1.4.1 解题思路

1.4.2 代码实现

module top_module (
    input clk,
    input reset,
    input enable,
    output [3:0] Q,
    output c_enable,
    output c_load,
    output [3:0] c_d
); 
    assign c_load = reset | Q[3] & Q[2] & enable;
    assign c_enable = enable;
    assign c_d = (1 == c_load) ? 4'b1 : 4'b0;
    count4 the_counter (clk, c_enable, c_load, c_d , Q);

endmodule

1.5 Counter 1000

从1000 Hz时钟中导出1 Hz信号，称为OneHertz，可用于驱动一组时/分/秒计数器的使能信号，以创建数字挂钟。由于我们希望时钟每秒计数一次，因此必须每秒准确地生成一个周期信号。使用模10（BCD）计数器和尽可能少的门电路构建分频器。还可以从你使用的每个BCD计数器输出启用信号（c_enable[0]表示最快的计数器，c_enable[2]表示最慢的计数器）。
提供以下BCD计数器。Enable必须拉高，计数器才能运行。Reset是同步信号，设置为高可强制使计数器清零。电路中的所有计数器必须直接使用相同的1000 Hz信号作为时钟。

module bcdcount (
	input clk,
	input reset,
	input enable,
	output reg [3:0] Q
);

1.5.1 解题思路

本题的核心在于考察分频电路的实现方式。基于题干信息，推荐使用BCD计数器和门电路来搭建分频电路，从1000 Hz的时钟频率分频到1 Hz的时钟信号，分频1000倍。解决本题需要思考下面几个问题：

• BCD计数器的计数周期为10，意味着可利用输出端的状态翻转检测周期的累加；
• 1000可利用十进制位数的拆分（$10\ast 10\ast 10$），使用三个BCD计数器的级联，实现1000的计数；
• 三个BCD计数器衔接部分的组合电路搭建，多级级联需要确保传导信号及时拉低（多信号关联）。

1.5.2 代码实现

module top_module (
    input clk,
    input reset,
    output OneHertz,
    output [2:0] c_enable
); //
    wire [3:0] counter0_Q;
    wire [3:0] counter1_Q;
    wire [3:0] counter2_Q;
    
    assign c_enable[0] = 1'b1;
    assign c_enable[1] = counter0_Q[0] & counter0_Q[3];
    assign c_enable[2] = counter1_Q[0] & counter1_Q[3] & c_enable[1];
    assign OneHertz = counter2_Q[0] & counter2_Q[3] & c_enable[2];
    
    bcdcount counter0 (clk, reset, c_enable[0], counter0_Q);
    bcdcount counter1 (clk, reset, c_enable[1], counter1_Q);
    bcdcount counter2 (clk, reset, c_enable[2], counter2_Q);
endmodule

1.6 4-digit decimal counter

构建一个4位BCD（二进制编码十进制）计数器。每个十进制数字使用4位编码：q[3:0]为个位数字，q[7:4]为十位数字，等等。对于数位[3:1]，还输出一个使能信号，指示高三位中的每一位何时增加。
你可能需要实例化或修改一位十进制计数器。

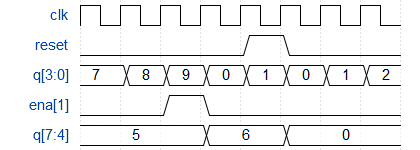
1.6.1 解题思路

本题在一个十进制计数器的基础上考察多位十进制计数器间的进位关系，如何借助低数位满十进一的状态使高数位自加是本题的设计核心。同时需要关注多数位自增关系，地位的进位状态需要及时消除以免导致高数位的错误自增。

1.6.2 代码实现

module dff_mod(
    input clk,
    input d,
    input ena,
    input reset,
    output reg q
);
    always @ (posedge clk)
        if(reset == 1)
            q <= 0;
        else if(ena == 1)
            q <= d;
endmodule

module bcd_module (
    input clk,
    input reset,      // Synchronous active-high reset
    input ena,
    output [3:0] q);

    wire [3:0] d;
    
    assign d[0] = ~q[0];
    assign d[1] = ~q[0] & q[1] | q[0] & ~q[1] & ~q[3];
    assign d[2] = ~q[1] & q[2] | ~q[0] & q[2] | q[0] & q[1] & ~q[2];
    assign d[3] = ~q[0] & q[3] | q[0] & q[1] & q[2];
    
    genvar i;
    generate
        for(i = 0; i < 4; i =i +1) begin: dff_loop
            dff_mod dff0(clk, d[i], ena, reset, q[i]);        
        end
    endgenerate
     
endmodule

module top_module (
    input clk,
    input reset,   // Synchronous active-high reset
    output [3:1] ena,
    output [15:0] q);
    
    assign ena[1] = q[3] & q[0];
    assign ena[2] = q[7] & q[4] & ena[1];
    assign ena[3] = q[11] & q[8] & ena[2];
    
    bcd_module bcd_mod0(clk, reset, 1'b1, q[3:0]);
    bcd_module bcd_mod1(clk, reset, ena[1], q[7:4]);
    bcd_module bcd_mod2(clk, reset, ena[2], q[11:8]);
    bcd_module bcd_mod3(clk, reset, ena[3], q[15:12]);
endmodule

1.7 12-hour clock

创建一组适合用作12小时时钟的计数器（带am/pm指示器）。您的计数器由快速运行的时钟进行计时，每当您的时钟增加时（即每秒一次），ena上都会有一个脉冲。
重置将时钟重置为12:00 AM。pm为0表示上午，1表示下午。hh、mm和ss是两个BCD（二进制编码十进制）数字，分别表示小时（01-12）、分钟（00-59）和秒（00-59）。重置的优先级高于使能，即使未使能，也可能发生重置。
以下时序图显示了从上午11:59:59到下午12:00:00的翻滚行为以及同步复位和使能行为。

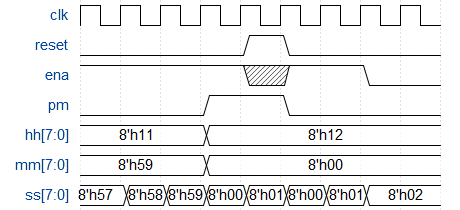
1.7.1 解题思路

本题重点考察多数制间的进位关系，时(hh)、分(mm)、**秒(ss)**三个时间单位中每个都需要使用两个BCD码来表示。分(mm)和秒(ss)都是满60进一，分成两个BCD码表示，低位的BCD码是满十进一，高位的BCD码是满六进一。**时(hh)**为满12循环一周，且一个状态的起始为01，难点在于两个BCD码如何表示，其中低位BCD码，计数满（10+2）次后重置为1，高位BCD码，初始为0，当低位BCD码计数到10时自加1，低位BCD计数满（10+2）后重置为0。

1.7.2 代码实现

module dfflr # (
    parameter DW = 32
)(
    input clk,
    input lden,
    input reset,      // Synchronous active-high reset
    input [DW-1:0] d,
    output [DW-1:0] q);
    
    always @ (posedge clk)
        if(1 == reset)
            q <= {DW{1'b0}};
        else if(1 == lden)
            q <= d;
endmodule

module dfflrs # (
    parameter DW = 32
)(
    input clk,
    input lden,
    input reset,      // Synchronous active-high reset
    input [DW-1:0] d,
    output [DW-1:0] q);
    
    always @ (posedge clk)
        if(1 == reset)
            q <= {{DW-1{1'b0}}, 1'b1};
        else if(1 == lden)
            q <= d;
endmodule

module count4 (
    input clk,
    input enable,
    input reset,      // Synchronous active-high reset
    input [3:0] d,
    output [3:0] q);
    always @ (posedge clk)
        if(1 == reset)
            q <= d;
        else if(1 == enable)
            q <= q + 1'b1;
endmodule

//计数器0~1，采取翻转方式实现；

//计数器1~12，采取例化+连线状态标志位；
module counter1_12_module (
    input clk,
    input reset,
    input enable,
    output [3:0] Q
); 
    
    wire c_load = reset | q[3] & q[2] & enable;
    wire c_enable = enable;
    wire [3:0] c_d = reset ? 4'b1100 : 4'b1;
    wire [3:0] q;
    
    assign Q = (q > 4'b1001) ? (q + 4'b0110) : q;
    
    count4 the_counter (.clk(clk), .enable(c_enable), .reset(c_load), .d(c_d) , .q(q));    
endmodule

//计数器0~5，采取例化+连线状态标志位；
module counter0_5_module (
    input clk,
    input reset,
    input enable,
    output [3:0] Q
); 
    wire c_load = reset | Q[0] & Q[2] & enable;
    wire c_enable = enable;
    wire [3:0] c_d = 4'b0;
    wire [3:0] q;
    assign Q = q;
    
    count4 the_counter (clk, c_enable, c_load, c_d , q);
endmodule

//计数器0~9，采取例化+连线状态标志位；
module counter0_9_module (
    input clk,
    input reset,
    input enable,
    output [3:0] Q
); 
    wire c_load = reset | Q[3] & Q[0] & enable;
    wire c_enable = enable;
    wire [3:0] c_d = 4'b0;
    wire [3:0] q;
    assign Q = q;
    
    count4 the_counter (clk, c_enable, c_load, c_d , q);
endmodule

module top_module(
    input clk,
    input reset,
    input ena,
    output pm,
    output [7:0] hh,
    output [7:0] mm,
    output [7:0] ss); 

    wire [5:0] inner_ena;
    assign inner_ena[0] = ena;
    assign inner_ena[1] = inner_ena[0] & ss[3] & ss[0];
    
    assign inner_ena[2] = inner_ena[1] & ss[6] & ss[4];
    assign inner_ena[3] = inner_ena[2] & mm[3] & mm[0];
    
    assign inner_ena[4] = inner_ena[3] & mm[6] & mm[4];
    assign inner_ena[5] = inner_ena[4] & (hh[3] & hh[0] | hh[4] & hh[1] & ~hh[0]);

    wire pm_en = inner_ena[4] & hh[4] & hh[0]; 
    wire [3:0] high4bit = (hh[3] & hh[0]) ? 4'b1 : 4'b0;
    //ss
    counter0_9_module ss_low4bit(clk, reset, inner_ena[0], ss[3:0]);
    counter0_5_module ss_high4bit(clk, reset, inner_ena[1], ss[7:4]);
    //mm
    counter0_9_module mm_low4bit(clk, reset, inner_ena[2], mm[3:0]);
    counter0_5_module mm_high4bit(clk, reset, inner_ena[3], mm[7:4]);
    //hh
    counter1_12_module hh_low4bit(clk, reset, inner_ena[4], hh[3:0]);
    dfflrs #(4) dfflr_hh_high4bit(clk, inner_ena[5], reset, high4bit, hh[7:4]);
    dfflr #(1) dfflr_pm(clk, pm_en, reset, ~pm, pm);
endmodule

2 shift registers

介绍Galois LFSR（linear feedback shift register）的原理。线性反馈移位寄存器（linear feedback shift register, LFSR)分为伽罗瓦 和斐波那契两种。
伽罗瓦：one-to-many（对内实现）；
斐波那契：many-to-one（对外实现）。
两者之间的转换关系？

2.1 4-bit shift register

2.2 Left/right rotator

2.3 Left/right arithmetic shift by 1 or 8

2.4 5-bit LFSR

2.5 3-bit LFSR

2.6 32-bit LFSR

2.6.1 解题思路

2.6.2 代码实现

module dff_module # (
    parameter DW =1
)(
    input clk,
    input reset,
    input [DW-1:0] d,
    output reg [DW-1:0] q
);
    always @ (posedge clk)
        if(reset == 1'b1)
            q <= {{DW-1{1'b0}}, 1'b1};
        else 
            q <= d; 
endmodule

module top_module(
    input clk,
    input reset,    // Active-high synchronous reset to 5'h1
    output [31:0] q
); 
    wire [31:0] data_pre;
    assign data_pre = {1'b0 ^ q[0], q[31:23], q[22] ^ q[0], q[21:3], q[2] ^ q[0], q[1] ^ q[0]};
    dff_module #(32) dff_mod0(.clk(clk), .reset(reset), .d(data_pre),.q(q));
endmodule

2.8

2.9 3-input LUT

2.9.1 解题思路

2.9.2 代码实现

module dff_module # (
    parameter DW = 1
)(
    input clk,
    input enable,
    input [DW-1:0] d,
    output reg [DW-1:0] q
);
    always @ (posedge clk)
        if(enable == 1'b1)
            q <= d;
endmodule

module top_module (
    input clk,
    input enable,
    input S,
    input A, B, C,
    output Z ); 
    
    wire [7:0] Q;
    wire [7:0] d_pre = {Q[6:0], S};
    assign Z = ~A&~B&~C ? Q[0] :
        ~A&~B&C ? Q[1] :
        ~A&B&~C ? Q[2] :
        ~A&B&C ? Q[3] :
        A&~B&~C ? Q[4] :
        A&~B&C ? Q[5] :
        A&B&~C ? Q[6] : Q[7];
    
    genvar i;
    generate
        for(i = 0; i < 8; i = i + 1) begin: dff_loop
            dff_module #(1) dff_mod0(
                .clk(clk),
                .enable(enable),
                .d(d_pre[i]),
                .q(Q[i]));
        end
    endgenerate
endmodule

3 More circuits

4 Finite state machines

4.1 simple FSM 1(asynchronous reset)

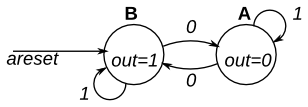
这是一个摩尔状态机，有两个状态，一个为A，一个为B。实现这个状态机。请注意，重置状态为B。
此练习与fsm1s相同，但使用异步重置。

4.1.1 解题思路

本题目的是实现moore时序电路，其输出信号仅仅取决于存储电路的状态。常用时序逻辑电路功能的表达方式有如下几种方式：

• 逻辑方程组：唯一确定时序电路功能，包含激励方程、状态转换方程、输出方程。激励方程由输入和存储电路状态的组合逻辑得到，状态转换方程由触发器的特性方程和激励方程组合得到，输出方程由存储电路状态（和输入：mealy型）的组合逻辑得到。
• 转换表、状态图：直观反应电路状态变化序列全过程；
• 时序图：仅能画出部分典型的波形图；
• HDL语言：抽象地刻画电路功能。

一般状态机的分析思路如下图所示：

4.1.2 代码实现

1. 标准三段式

• 首先，根据状态机的个数确定状态机编码。利用编码给状态寄存器赋值，代码可读性更好。
• 状态机第一段（状态转换方程），时序逻辑，非阻塞赋值，传递寄存器的状态。
• 状态机第二段（激励方程），组合逻辑，阻塞赋值，根据当前状态和当前输入，确定下一个状态机的状态。
• 状态机第三代（输出方程），时序逻辑，非阻塞赋值（Mealy 型）或者阻塞赋值（Moore型），根据当前状态和当前输入，确定输出信号。

module top_module(
    input clk,
    input areset,    // Asynchronous reset to state B
    input in,
    output out);//  
    
    //machine state decode
    parameter A = 1'b0;
    parameter B = 1'b1; 
    //machine variable
    reg cur_state;
    reg next_state;

    //(1) state transfer, DFF:q <= d; ==> d = cur_state; 
    always @(posedge clk or posedge areset) begin    // This is a sequential always block
        // State flip-flops with asynchronous reset
        if(areset == 1'b1)
            cur_state <= 1'b1;
        else
            cur_state <= next_state;
    end
    //(2) Excitation equation, combinational logic
    always @(*) begin    // This is a combinational always block
        // State transition logic
        case(cur_state)
            A: next_state = in ? A : B;
            B: next_state = in ? B : A;
            default: next_state = B;
        endcase
    end

    //(3) output logic:
    //mealy sequence logic using non-block assignment
    //moore sequence logic using block assignment
    assign out = cur_state;

endmodule

2. 基于D触发器

module top_module(
    input clk,
    input areset,    // Asynchronous reset to state B
    input in,
    output out);//  

    reg q;
    wire d = ~q ^ in;
    
    always @(posedge clk, posedge areset) begin    // This is a sequential always block
        // State flip-flops with asynchronous reset
        if(areset == 1'b1)
            q <=  1'b1;
        else 
            q <= d;   
    end

    assign out = q;
endmodule

4.2 Simple FSM 1(synchronous reset)

4.2.1 解题思路

4.2.2 代码实现

• 基于T触发器

// Note the Verilog-1995 module declaration syntax here:
module tff_module # (
    parameter DW = 1
)(
    input clk,
    input reset,
    input [DW-1:0] d,
    output reg [DW-1:0] q
);
    always @ (posedge clk)
        if(reset == 1'b1)
            q <= {{DW-1{1'b0}}, 1'b1};
        else if(d == 1'b0)
            q <= ~q;
endmodule

module top_module(clk, reset, in, out);
    input clk;
    input reset;    // Synchronous reset to state B
    input in;
    output out;//  
    reg out;
    
    tff_module #(1) tff_mod0(.clk(clk), .d(in), .reset(reset), .q(out));

endmodule

4.9 Design a Moore FSM

4.9.1 解题思路

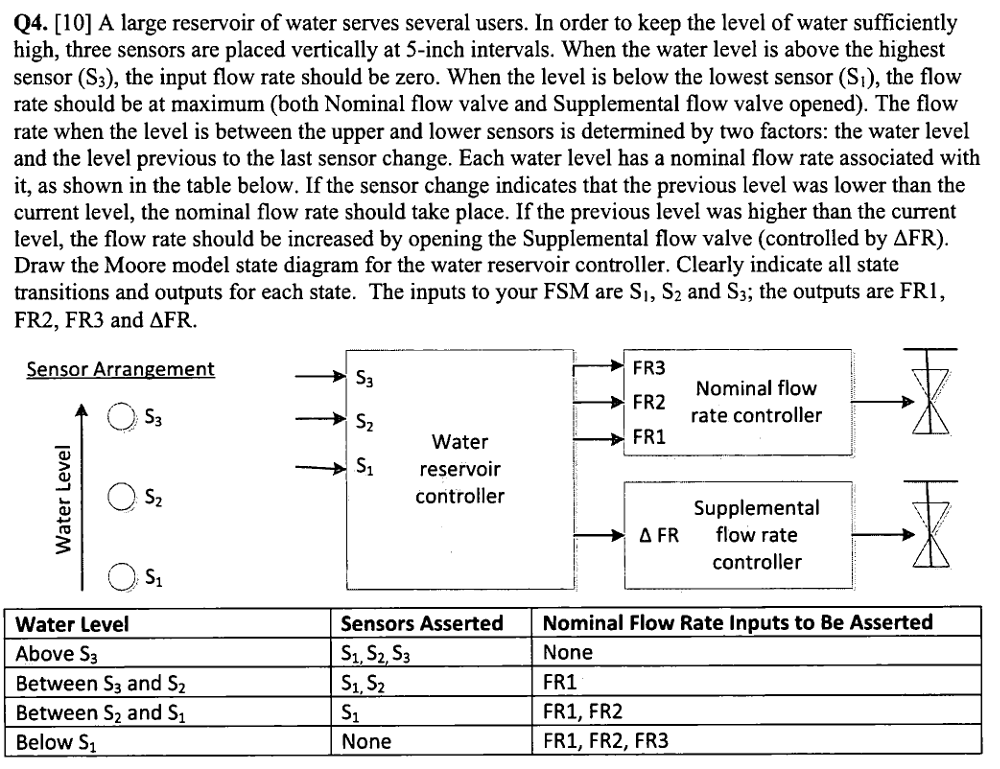
本题包含两类输出，其一为名义流速率控制器相关联的标识位，该类标识的具体输出由状态机当前状态来决定，根据题设基本可以分成四种状态下的取值场景，典型的摩尔状态机，与输入无关；其二为补充流速率控制器相关联的标识位，该类标识的具体输出既由当前状态又由输入共同决定，典型的米利状态机。
由于题设需要设计一个摩尔型状态机，因此补充流速率控制器也需要将米利状态机转变位摩尔状态机。Mealy状态机转变为Moore状态机的思路是采用更多状态来表示输入的差异，即Mealy状态+输入=》Moore状态。

4.9.2 代码实现

下面给出两种实现方式，两种方法都不是常用三段式解决方法，而是借助与D触发器来描述状态变化。

方法一：
该解题方法可以概括为如下：

module dff_module # (
    parameter DW = 1
)(
    input clk,
    input reset,
    input en,
    input [DW-1:0] d,
    output reg [DW-1:0] q
);
    always @ (posedge clk)
        if(reset == 1'b1)
            q <= {{DW-1{1'b0}}, 1'b1};
        else if(en == 1'b1)
            q <= d;
endmodule

module top_module (
    input clk,
    input reset,
    input [3:1] s,
    output fr3,
    output fr2,
    output fr1,
    output dfr
); 
    wire s_000 = (s == 3'b000);
    wire s_001 = (s == 3'b001);
    wire s_011 = (s == 3'b011);
    wire s_111 = (s == 3'b111);
    
    localparam FLOW_CTRL_STATE_WIDTH = 3;
    
    wire [FLOW_CTRL_STATE_WIDTH-1:0] flow_ctrl_state_next;
    wire [FLOW_CTRL_STATE_WIDTH-1:0] flow_ctrl_state_r;
    wire flow_ctrl_state_ena;
    
    //State 0:The 0th state, means this is initial state, s = 000, delta FR = 0;
    localparam FLOW_CTRL_STATE_0TH = 3'd0;
    //State 1:The 1th state, s = 000, delta FR = 1;
    localparam FLOW_CTRL_STATE_1TH = 3'd1;
    //State 2:The 2th state, s = 001, delta FR = 0;
    localparam FLOW_CTRL_STATE_2TH = 3'd2;
    //State 3:The 3th state, s = 001, delta FR = 1;
    localparam FLOW_CTRL_STATE_3TH = 3'd3;
    //State 4:The 4th state, s = 011, delta FR = 0;
    localparam FLOW_CTRL_STATE_4TH = 3'd4;
    //State 5:The 5th state, s = 011, delta FR = 1;
    localparam FLOW_CTRL_STATE_5TH = 3'd5;
    //State 6:The 6th state, s = 111, delta FR = 0;
    localparam FLOW_CTRL_STATE_6TH = 3'd6;    
    
    wire [FLOW_CTRL_STATE_WIDTH-1:0] state_0th_nxt;
    wire [FLOW_CTRL_STATE_WIDTH-1:0] state_1th_nxt;
    wire [FLOW_CTRL_STATE_WIDTH-1:0] state_2th_nxt;
    wire [FLOW_CTRL_STATE_WIDTH-1:0] state_3th_nxt;
    wire [FLOW_CTRL_STATE_WIDTH-1:0] state_4th_nxt;
    wire [FLOW_CTRL_STATE_WIDTH-1:0] state_5th_nxt;
    wire [FLOW_CTRL_STATE_WIDTH-1:0] state_6th_nxt;
    
    wire state_0th_exit_ena;
    wire state_1th_exit_ena;
    wire state_2th_exit_ena;
    wire state_3th_exit_ena;
    wire state_4th_exit_ena;
    wire state_5th_exit_ena; 
    wire state_6th_exit_ena; 
    
    // Define some common signals and reused later to save gatecounts
    wire flow_ctrl_sta_is_0th = (flow_ctrl_state_r == FLOW_CTRL_STATE_0TH);
    wire flow_ctrl_sta_is_1th = (flow_ctrl_state_r == FLOW_CTRL_STATE_1TH);
    wire flow_ctrl_sta_is_2th = (flow_ctrl_state_r == FLOW_CTRL_STATE_2TH);
    wire flow_ctrl_sta_is_3th = (flow_ctrl_state_r == FLOW_CTRL_STATE_3TH);
    wire flow_ctrl_sta_is_4th = (flow_ctrl_state_r == FLOW_CTRL_STATE_4TH);
    wire flow_ctrl_sta_is_5th = (flow_ctrl_state_r == FLOW_CTRL_STATE_5TH);
    wire flow_ctrl_sta_is_6th = (flow_ctrl_state_r == FLOW_CTRL_STATE_6TH);
    
    assign state_0th_exit_ena = flow_ctrl_sta_is_0th & (s_001 | s_011 | s_111);
    assign state_0th_nxt      = s_001 ? FLOW_CTRL_STATE_2TH :
                                s_011 ? FLOW_CTRL_STATE_4TH :
                                s_111 ? FLOW_CTRL_STATE_6TH : FLOW_CTRL_STATE_0TH;
    
    assign state_1th_exit_ena = flow_ctrl_sta_is_1th & (s_001 | s_011 | s_111);
    assign state_1th_nxt      = s_001 ? FLOW_CTRL_STATE_2TH :
                                s_011 ? FLOW_CTRL_STATE_4TH :
                                s_111 ? FLOW_CTRL_STATE_6TH : FLOW_CTRL_STATE_1TH;  
    
    assign state_2th_exit_ena = flow_ctrl_sta_is_2th & (s_000 | s_011 | s_111);
    assign state_2th_nxt      = s_000 ? FLOW_CTRL_STATE_1TH :
                                s_011 ? FLOW_CTRL_STATE_4TH :
                                s_111 ? FLOW_CTRL_STATE_6TH : FLOW_CTRL_STATE_2TH;   
    
    assign state_3th_exit_ena = flow_ctrl_sta_is_3th & (s_000 | s_011 | s_111);
    assign state_3th_nxt      = s_000 ? FLOW_CTRL_STATE_1TH :
                                s_011 ? FLOW_CTRL_STATE_4TH :
                                s_111 ? FLOW_CTRL_STATE_6TH : FLOW_CTRL_STATE_3TH;

    assign state_4th_exit_ena = flow_ctrl_sta_is_4th & (s_000 | s_001 | s_111);
    assign state_4th_nxt      = s_000 ? FLOW_CTRL_STATE_1TH :
                                s_001 ? FLOW_CTRL_STATE_3TH :
                                s_111 ? FLOW_CTRL_STATE_6TH : FLOW_CTRL_STATE_4TH;  
    
    assign state_5th_exit_ena = flow_ctrl_sta_is_5th & (s_000 | s_001 | s_111);
    assign state_5th_nxt      = s_000 ? FLOW_CTRL_STATE_1TH :
                                s_001 ? FLOW_CTRL_STATE_3TH :
                                s_111 ? FLOW_CTRL_STATE_6TH : FLOW_CTRL_STATE_5TH;   
    
    assign state_6th_exit_ena = flow_ctrl_sta_is_6th & (s_000 | s_001 | s_011);
    assign state_6th_nxt      = s_000 ? FLOW_CTRL_STATE_1TH :
                                s_001 ? FLOW_CTRL_STATE_3TH :
                                s_011 ? FLOW_CTRL_STATE_5TH : FLOW_CTRL_STATE_6TH;   
    
    assign flow_ctrl_state_ena = state_0th_exit_ena 
        | state_1th_exit_ena  
        | state_2th_exit_ena  
        | state_3th_exit_ena  
        | state_4th_exit_ena
        | state_5th_exit_ena
        | state_6th_exit_ena; 
    
    assign flow_ctrl_state_next = ({FLOW_CTRL_STATE_WIDTH{state_0th_exit_ena}} & state_0th_nxt)
        | ({FLOW_CTRL_STATE_WIDTH{state_1th_exit_ena}} & state_1th_nxt)
        | ({FLOW_CTRL_STATE_WIDTH{state_2th_exit_ena}} & state_2th_nxt)
        | ({FLOW_CTRL_STATE_WIDTH{state_3th_exit_ena}} & state_3th_nxt)
        | ({FLOW_CTRL_STATE_WIDTH{state_4th_exit_ena}} & state_4th_nxt)
        | ({FLOW_CTRL_STATE_WIDTH{state_5th_exit_ena}} & state_5th_nxt)
        | ({FLOW_CTRL_STATE_WIDTH{state_6th_exit_ena}} & state_6th_nxt);
    
    dff_module #(FLOW_CTRL_STATE_WIDTH) dff_mod0(clk, reset, flow_ctrl_state_ena, flow_ctrl_state_next, flow_ctrl_state_r);
    
    assign dfr = flow_ctrl_sta_is_1th | flow_ctrl_sta_is_3th | flow_ctrl_sta_is_5th;
    assign fr1 = flow_ctrl_sta_is_0th 
        | flow_ctrl_sta_is_1th
        | flow_ctrl_sta_is_2th 
        | flow_ctrl_sta_is_3th 
        | flow_ctrl_sta_is_4th 
        | flow_ctrl_sta_is_5th;
    
    assign fr2 = flow_ctrl_sta_is_0th 
        | flow_ctrl_sta_is_1th
        | flow_ctrl_sta_is_2th 
        | flow_ctrl_sta_is_3th;
    
    assign fr3 = flow_ctrl_sta_is_0th | flow_ctrl_sta_is_1th;   
endmodule

方法二
米利状态机表示，对输出加一级触发器，打一拍来保证输入与时钟同步切换。

module dff_module1 # (
    parameter DW = 1
)(
    input clk,
    input reset,
    input [DW-1:0] d,
    output reg [DW-1:0] q
);
    always @ (posedge clk)
        if(reset == 1'b1)
            q <= {DW{1'b1}};
        else
            q <= d;
endmodule

module dff_module0 # (
    parameter DW = 1
)(
    input clk,
    input reset,
    input [DW-1:0] d,
    output reg [DW-1:0] q
);
    always @ (posedge clk)
        if(reset == 1'b1)
            q <= {DW{1'b0}};
        else
            q <= d;
endmodule

module top_module (
    input clk,
    input reset,
    input [3:1] s,
    output fr3,
    output fr2,
    output fr1,
    output dfr
); 
    wire s_000 = (s == 3'b000) ? 1'b1 : 1'b0;
    wire s_001 = (s == 3'b001) ? 1'b1 : 1'b0;
    wire s_011 = (s == 3'b011) ? 1'b1 : 1'b0;
    wire s_111 = (s == 3'b111) ? 1'b1 : 1'b0;
    wire fr1_next = s_000 | s_001 | s_011;
    wire fr2_next = s_000 | s_001;
    wire fr3_next = s_000;
    dff_module1 #(3) dff_mod1_0(clk, reset, {fr1_next, fr2_next, fr3_next}, {fr1, fr2, fr3});
    
    wire [1:0] q_r;
    wire [1:0] q_next = s_000 ? 2'b00 : 
                        s_001 ? 2'b01 : 
                        s_011 ? 2'b10 : 
                        s_111 ? 2'b11 : q_r;
    wire dfr_next = (~q_next[0] & ~q_next[1]) | (q_r[1] & ~q_next[1]) | (q_r[1] & q_r[0] & ~q_next[0]);
    wire dfr_pre = (q_next == q_r) ? dfr : dfr_next;
    dff_module1 #(1) dff_mod1_1(clk, reset, dfr_pre, dfr);
    
    dff_module0 #(2) dff_mod0_1(clk, reset, q_next, q_r);

endmodule

最后

以上就是饱满玉米为你收集整理的HDLbits系列解题分析1 Counters2 shift registers3 More circuits4 Finite state machines的全部内容，希望文章能够帮你解决HDLbits系列解题分析1 Counters2 shift registers3 More circuits4 Finite state machines所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。