目录
前言:
一、时序逻辑电路概述
1.异步时序电路和同步时序电路
2.状态机
1)、状态转换表;
2)、状态转换图:
自启动:
摩尔状态机与米利状态机的状态转换表的轻微区别:
前言:
这一章节和上一章触发器的联系较为密切,有兴趣的同学们可以先看一下我前面文章
被数电老师痛斥期中试卷后的数电知识总结(三):触发器_靳小锅er的博客-CSDN博客
一、时序逻辑电路概述
1.异步时序电路和同步时序电路
时序逻辑电路主要分为两种:同步时序电路和异步时序电路。
同步时序电路和异步时序电路其实很好分辨:我们从名字上就可以得知其不同在于时序,
如同我们可以得知同步时序电路就是指其电路种的触发器只受一个时钟源信号(CP)控制,同样的异步时序电路就是其电路中的触发器受多个时钟源信号(CP)控制。

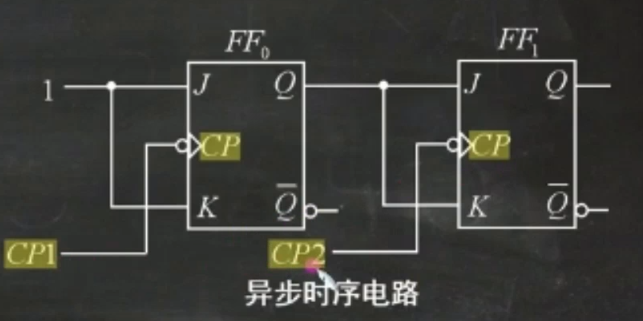
2.状态机
鉴于时序电路在工作时是在电路的有限个状态间按一定的规律转换的,所以又将时序电路称为状态机(State Machine),优先状态机(FINITE SM)或算法状态机(Algorithmic SM)。
了解过FPGA的同学应该略有耳闻,状态机又被称为FPGA的灵魂,从头到尾贯彻整个FPGA的设计。
状态机是FPGA设计中一种非常重要、非常根基的设计思想,堪称FPGA的灵魂,贯穿FPGA设计的始终。简单地说,状态机就是一副描绘着状态变迁的状态转移图,它体现着系统对外界事件的反应和行为。(这里不再多讲状态机在FPGA和单片机内的实际应用了,有时间博主会另外新开一篇专门写状态机在STM32上的应用,这里不再深入)。
在数字系统中有两大类有限状态机(Finite State Machine,FSM),分别如下:
第一种 Mealy型: 米利(Mealy)机的下一个状态和输出取决于 当前状态和当前输入。
第二种 Moore型:摩尔(Moore)机 的下一个状态取决于当前状态和当前输入, 但其输出仅取决于 当前状态。
其实客观上来看摩尔状态机其实算是米利状态机的一种特殊情况(当输入信号不影响输出逻辑的时候)

讲到状态机在数电里的考点主要是考察大家对于时序逻辑电路的状态转换表,状态转换图,状态机流程图和时序图。
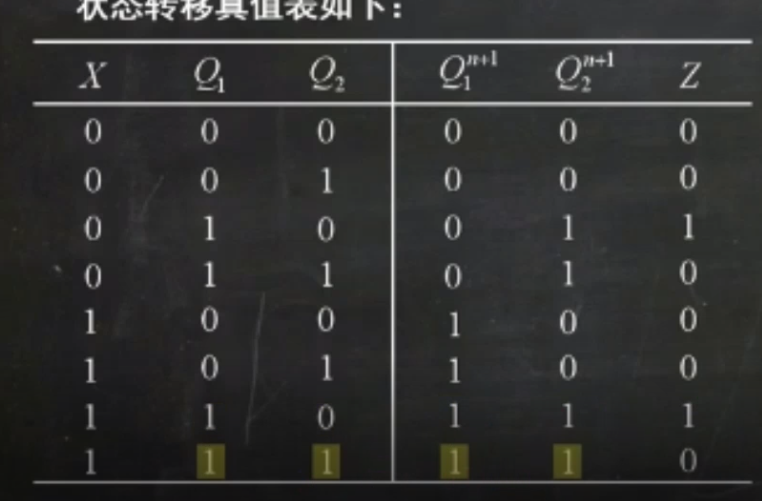
上面所说的不管是状态转换表还是状态转换图以及后面的流程图和时序图其实根本上都是根本上都不过是有下面这几种东西推导出来的:激励(输入信号),输出方程和状态方程
首先来看一道课本例题:


1)、状态转换表;
我更喜欢把它当成电路的信号真值表
其实就相当于根据上面的输出方程和状态方程,代入输入量Q1,Q2,Q3画出的真值表

2)、状态转换图:
其实状态转换图其实更好理解,就是状态转换表的另一种变换,简单来说就是根据状态转换表的第一行输入(默认)为状态转换图的起始点,以其触发器的输出端的状态作为第二个节点,之后找到在转换表里与其相状态的的状态输入,再找到其对应的输出端的状态作为第三个节点,如此反复,如果到状态转换图按照上述操作画最后,状态转换表里的输入量仍有未作为节点作图的话,那就以此输入量为节点继续画状态转换图。
比如上述例题的状态转换图为:【0 0 0】->[0 0 1 ] ->[0 1 0 ]-> [0 1 1]-> [1 0 0]-> [1 0 1]-> [1 1 0],但是此时未用到111 所以需补上 【1 1 1】 所以最终答案应该是【1 1 1】->[0 0 0】->[0 0 1 ] ->[0 1 0 ]-> [0 1 1]-> [1 0 0]-> [1 0 1]-> [1 1 0]->[0 0 0]。如下图
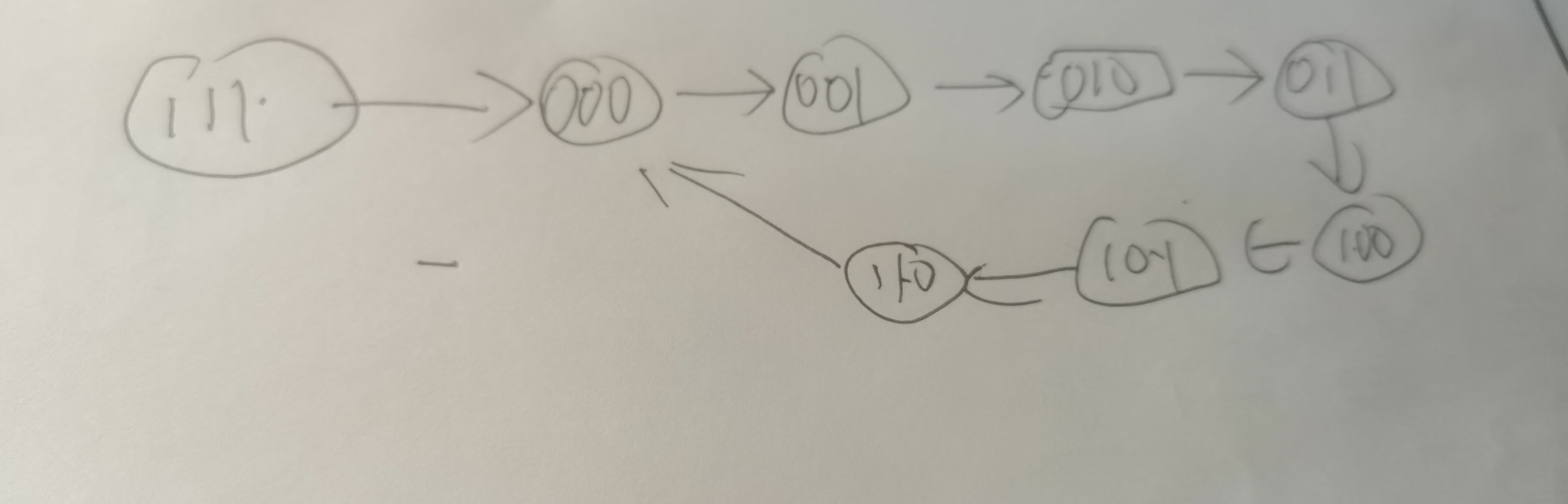
如果我们分析的时序电路是无输入和无输出的电路的话,一般多为计数器,而一般电路的输入进制主要参考状态转换图里的闭环节点数目,比如上图假设其没有输出,单纯作为计数器来使用的话,那就是一个七进制计数器。
下面分享一下处理这种问题的步骤:

自启动:
顺便说一下有关自启动的问题,如果当电路状态转换图只有一个闭环的时候,那么此时电路具有自启动能力,反之,如果有两个以及两个以上的闭环的时候,那么电路不具有自启动能力。
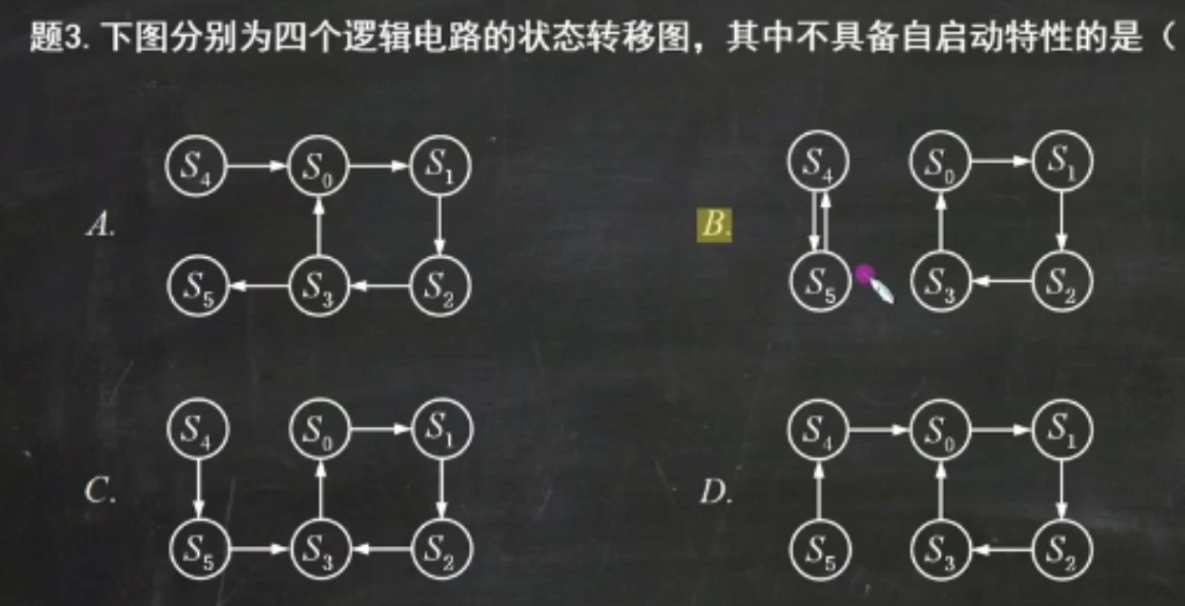
如图B就不具有自启动特性
摩尔状态机与米利状态机的状态转换表的轻微区别:
摩尔状态机由于其输入信号不影响输出,所以摩尔状态机的状态转换图和状态转换表的输出端不需要分析输入。
直接上图对比吧,说起来太难理解了
摩尔:

米利
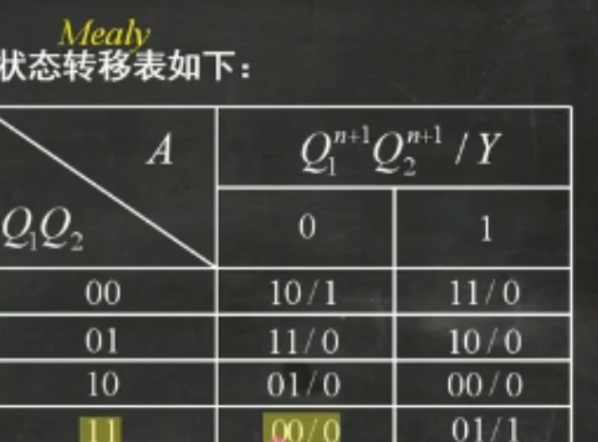
最后
以上就是淡定红牛最近收集整理的关于被数电老师痛斥期中试卷后的数电知识总结(四):时序逻辑电路的分析与设计 前言:一、时序逻辑电路概述1.异步时序电路和同步时序电路的全部内容,更多相关被数电老师痛斥期中试卷后内容请搜索靠谱客的其他文章。








发表评论 取消回复