逻辑代数基础

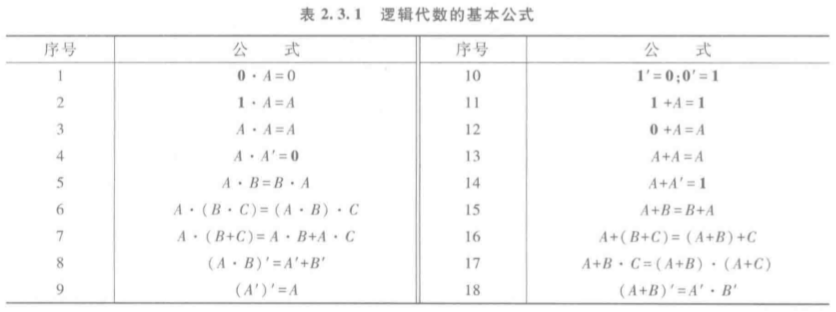
一、逻辑代数基本公式：

二、逻辑代数基本定理：

(1)、代入定理：在任何一个包含变量A的逻辑等式中，若以另外一个逻辑式代入式中的所有A的位置，则等式仍然成立，称为代入定理。

(2)、反演定理：对于任何一个逻辑式Y，若将其中所有的“·”换成“+”，“+”换成“·”，0换成1，1换成0，原变量换成反变量，反变量换成原变量，则得到的结果就是Y‘。称这个规律为反演定律。反演定律需要遵循两个基本原则：①仍需遵循先括号、然后乘、最后加的运算优先次序。②不属于单个变量上的反号应保留不变。

(3)、对偶定理：若两个逻辑式相等，则它们的对偶式也相等，称为对偶定理。所谓对偶式：对于任何一个逻辑式Y，将其中的“·”换成“+”，"+"换成“·”，0换成1，1换成0，则得到一个新的逻辑式Yd，称这个Yd就是Y的对偶式。

三、逻辑函数描述方法：

(1)、逻辑函数式：将输出与输入之间的逻辑关系写成与、或、非等运算的组合式，即逻辑代数式，得到所需要的逻辑函数式。

(2)、真值表：将输入变量所有的取值下对应的输出值找出来，列成表格，即可得到真值表。

(3)、逻辑图：将逻辑函数式中各变量之间的与、或、非等逻辑关系用图形符号表示出来，就可以画出描述函数关系的逻辑图。

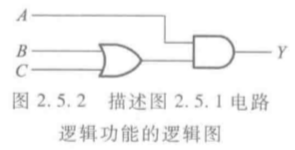
(4)、波形图(时序图)：如果将逻辑函数输入变量每一种可能出现的取值与对应的输出值按时间顺序依次排列起来，就得到了描述该逻辑函数的波形图，又称为时序图。

(5)、卡诺图：将n变量的全部最小项各用一个小方块表示，并使具有逻辑相邻性的最小项在几何位置上也相邻地排列起来，所得到的图像称为n变量最小项的卡诺图。

(6)、硬件描述语言(HDL)：主要包括Verilog语言和VHDL语言两种。

四、逻辑函数两种标准形式：

(1)、最小项之和：在n变量逻辑函数中，若m为包含了n个因子的乘积项，而且这n个变量均以原变量或反变量的形式在m中出现一次，则称m为该组变量的最小项。n变量的最小项应有个。

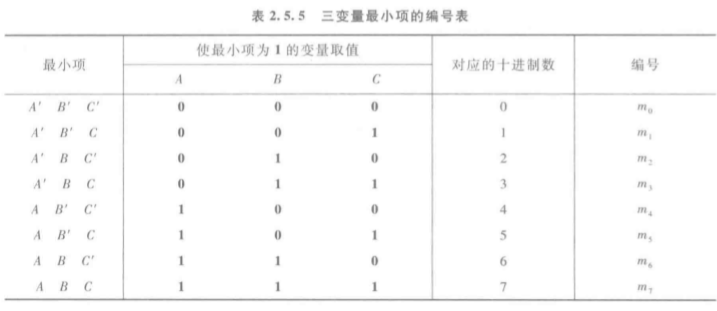
最小项重要性质：

①、在输入变量的任何取值下必有一个最小项，而且仅有一个最小项的值为1。

②、全体最小项之和为1。

③、任意两个最小项的乘积为0。

④、具有相邻性的两个最小项之和可以合并成一项并消去一对因子。

(2)、最大项之积：在n变量逻辑函数中，若M为n个变量之和，而且这n个变量均已原变量或反变量的形式在M中出现一次，则称M为该组变量的最大项。n变量的最大项应有个。

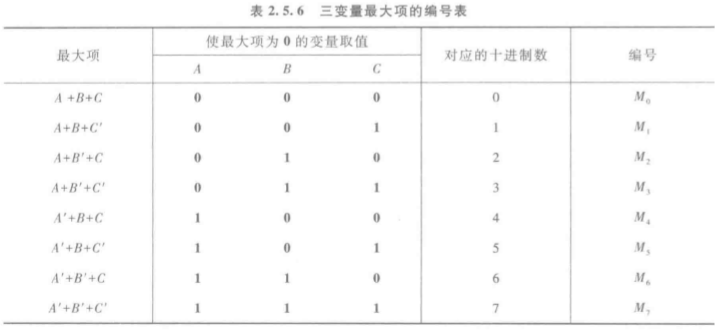
最大项重要性质：

①、在输入变量的任何取值下必有一个最大项，而且只有一个最大项的值为0。

②、全体最大项之积为0。

③、任意两个最大项之和为1。

④、只有一个变量不同的两个最大项的乘积等于各相同变量之和。

五、逻辑函数化简方法：

在与或逻辑函数式中，若其中包含的乘积项已经最少，而且每个乘积项里的因子也不能再减少时，则称此逻辑函数式为最简形式。化简逻辑函数的目的就是要消去多余的乘积项和每个乘积项中多余的因子，以得到逻辑函数式的最简形式。

(1)、公式化简法：就是反复使用逻辑代数的基本公式和常用公式消去函数式中多余的乘积项和多余的因子，以求得函数式得最简形式。

(2)、卡诺图化简法：是一种基于合并最小项的化简方法。

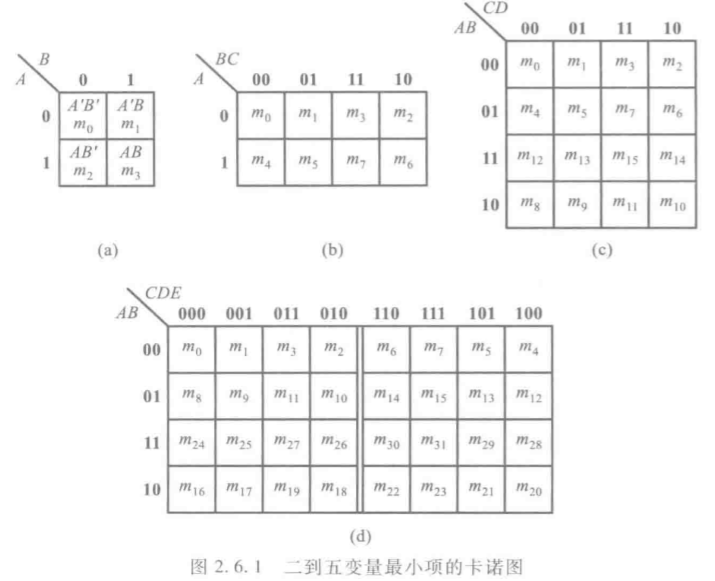
卡诺图化简法的原则与步骤：如果有个最小项相邻(n=1,2,...)并排列成一个矩形组，则它们可以合并为一项，并消去n对因子，合并后的结果中仅仅包含这些最小项的公共因子。

①、将函数化为最小项之和的形式。

②、画出表示该逻辑函数的卡诺图。

③、找出可以合并的最小项。

④、选取化简后的乘积项。选取的原则是：

Ⅰ、这些乘积项应包含函数式中所有的最小项(应覆盖卡诺图中所有的1)。

Ⅱ、所用的乘积项数目最少。也就是可合并的最小项组成的矩形组数目最少。

Ⅲ、每个乘积项包含的因子最少。也就是每个可合并的最小项矩形组中应包含尽量多的最小项。

最后

以上就是欣喜雨为你收集整理的逻辑代数基础的全部内容，希望文章能够帮你解决逻辑代数基础所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。