一位全加器
输入信号:A和B为加法器的两个输入,Ci进位信号,S为加数和的输出,Co表示向高位的进位信号。则可得到如下一位全加器真值表
| A | B | Ci | S | Co |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
类似于十进制加法的逢十进一,二进制加法则是逢二进一。通过上述真值表化简得到加法和S和进位信号的表达式。
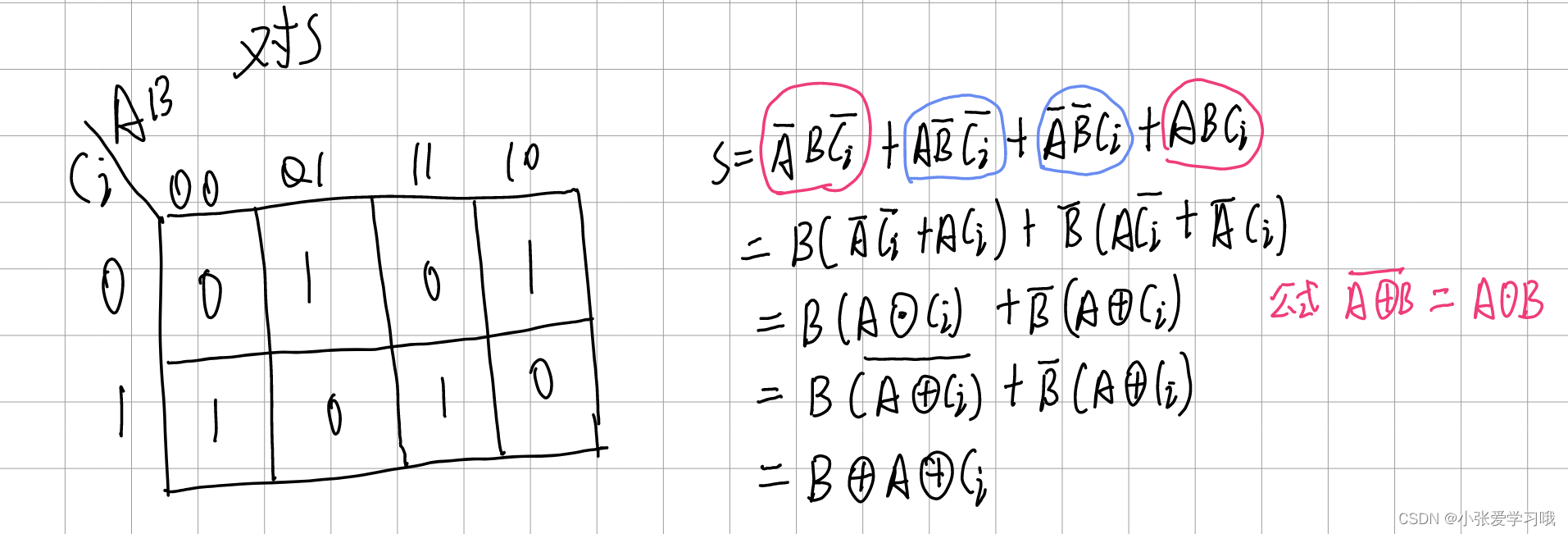
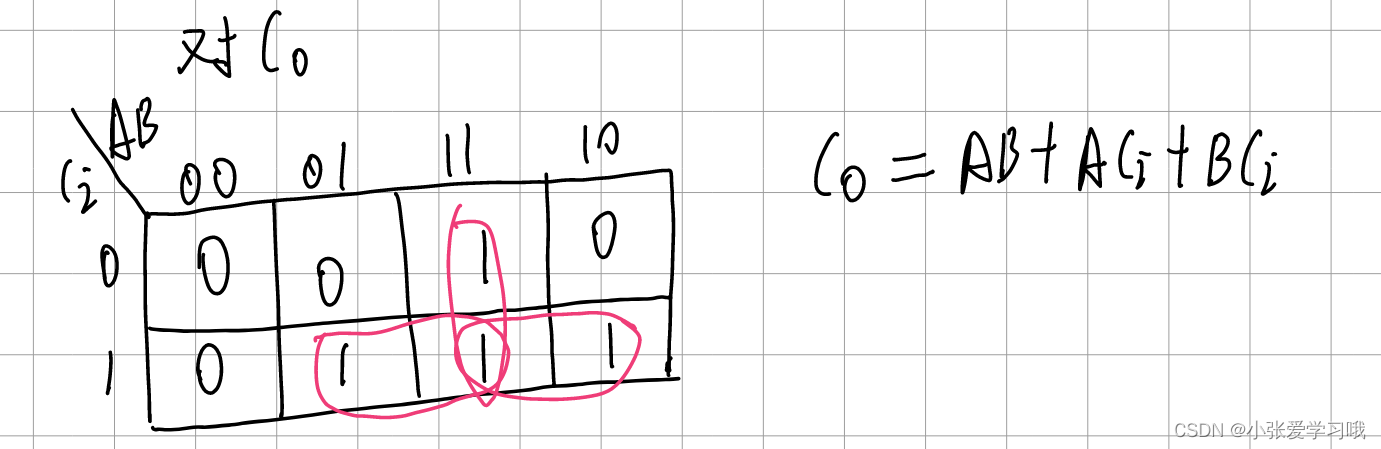
综合出来的电路如下:
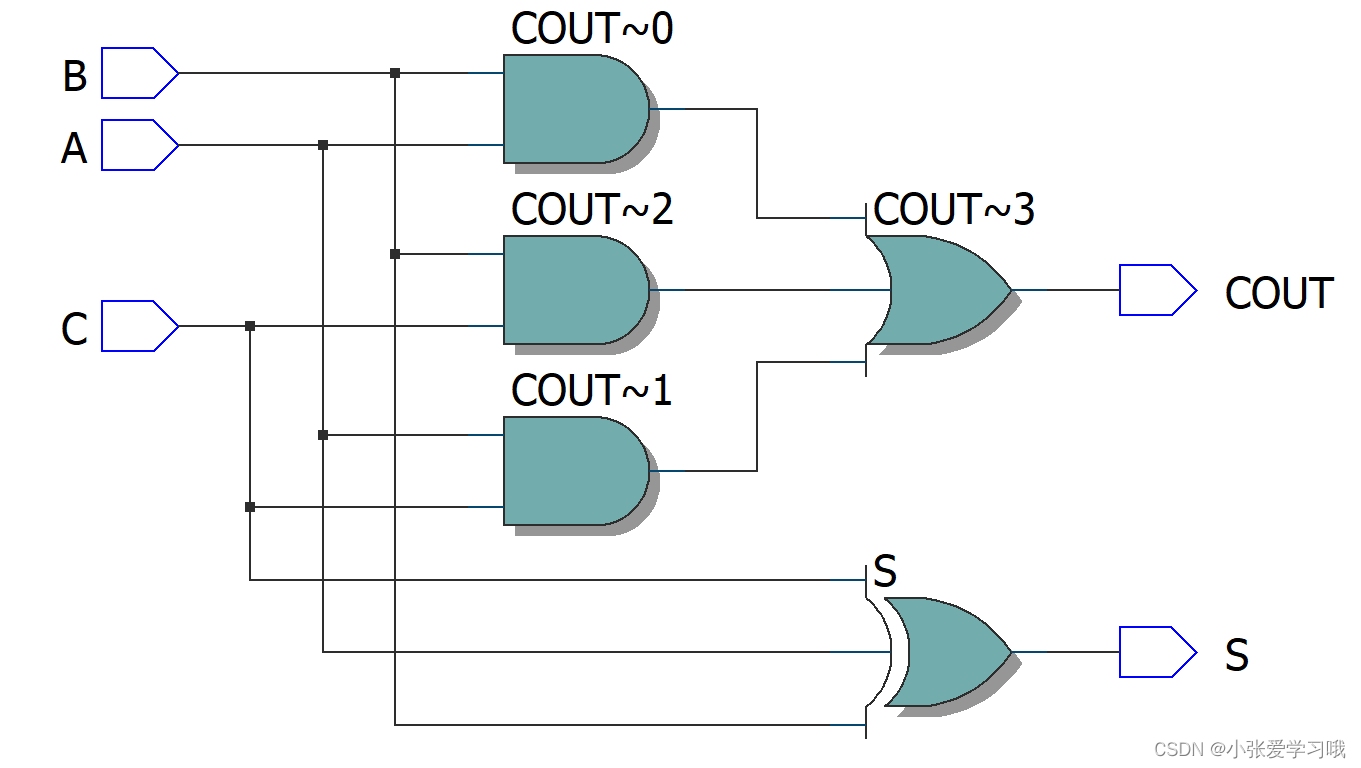
8位串行加法器
如果要实现8位串行加法器本质上其实就是把我们上面的一位全加器调用8次,每一个全加器输出的进位信号作为下一个全加器的输入进位信号,最终综合就得到如下电路:
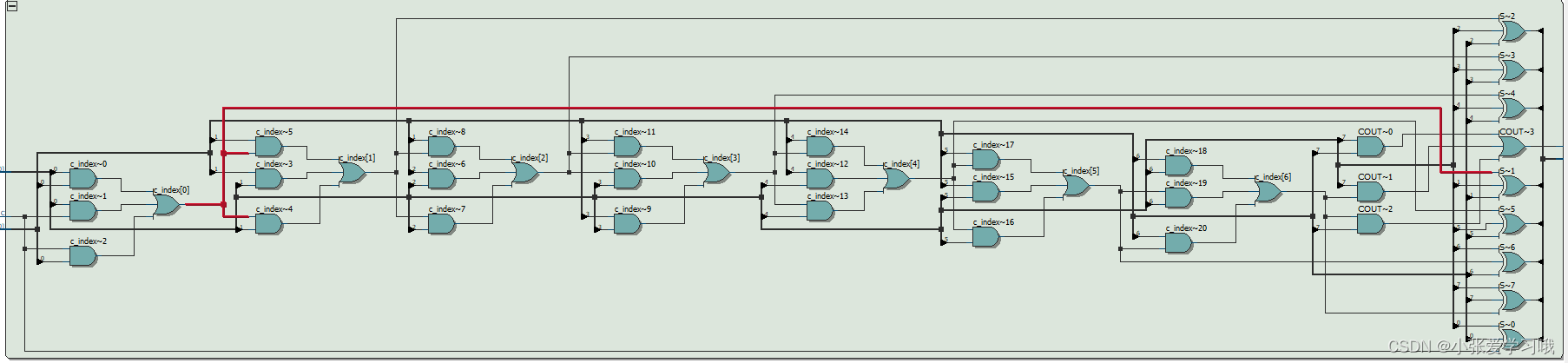
从性能上看,由于下一位的计算需要前一位的进位信号准备好才能计算出正确的结果,因此串行加法器相对来说计算需要的时间就很长。而造成这一问题的主要原因在于进位信号是串行产生的。如果要优化加法器,则需要从进位链上优化。对于一个多位的加法器,输入的加数A和B都是已知的,那么如果缩短进位时间,则相应的计算最终结果也会更快一点。下面介绍一种性能相对优秀一点的加法器:进位旁路加法器。
进位旁路加法器
通过对上述一位全加器真值表的进位输出信号观察分析可以得出以下三种情况:
- 当两个输入A和B都是1时,则向高位的进位信号Co一定为1。
- 当两个输入A和B都是0时,则向高位的进位信号Co一定为0。
- 当两个输入A和B不相等时,则向高位的进位信号Co完全由Ci决定。
这里引出如下三个信号:G(generate)进位产生信号、D(delete)进位删除信号、P(propagate)进位传播信号。得到如下关系式:
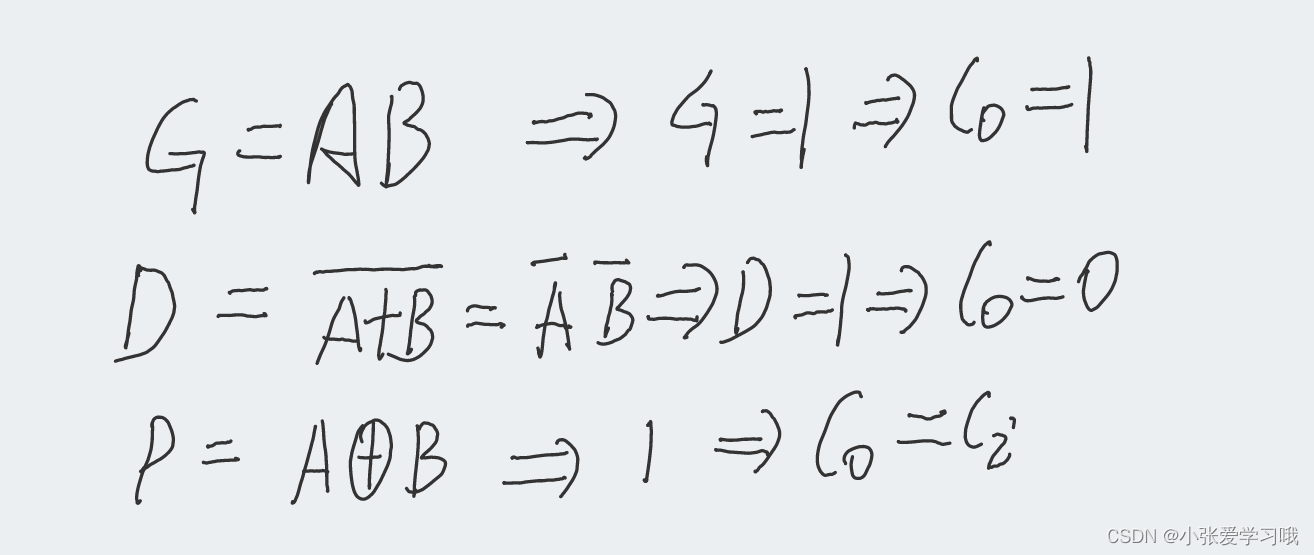
进位旁路结构如下:
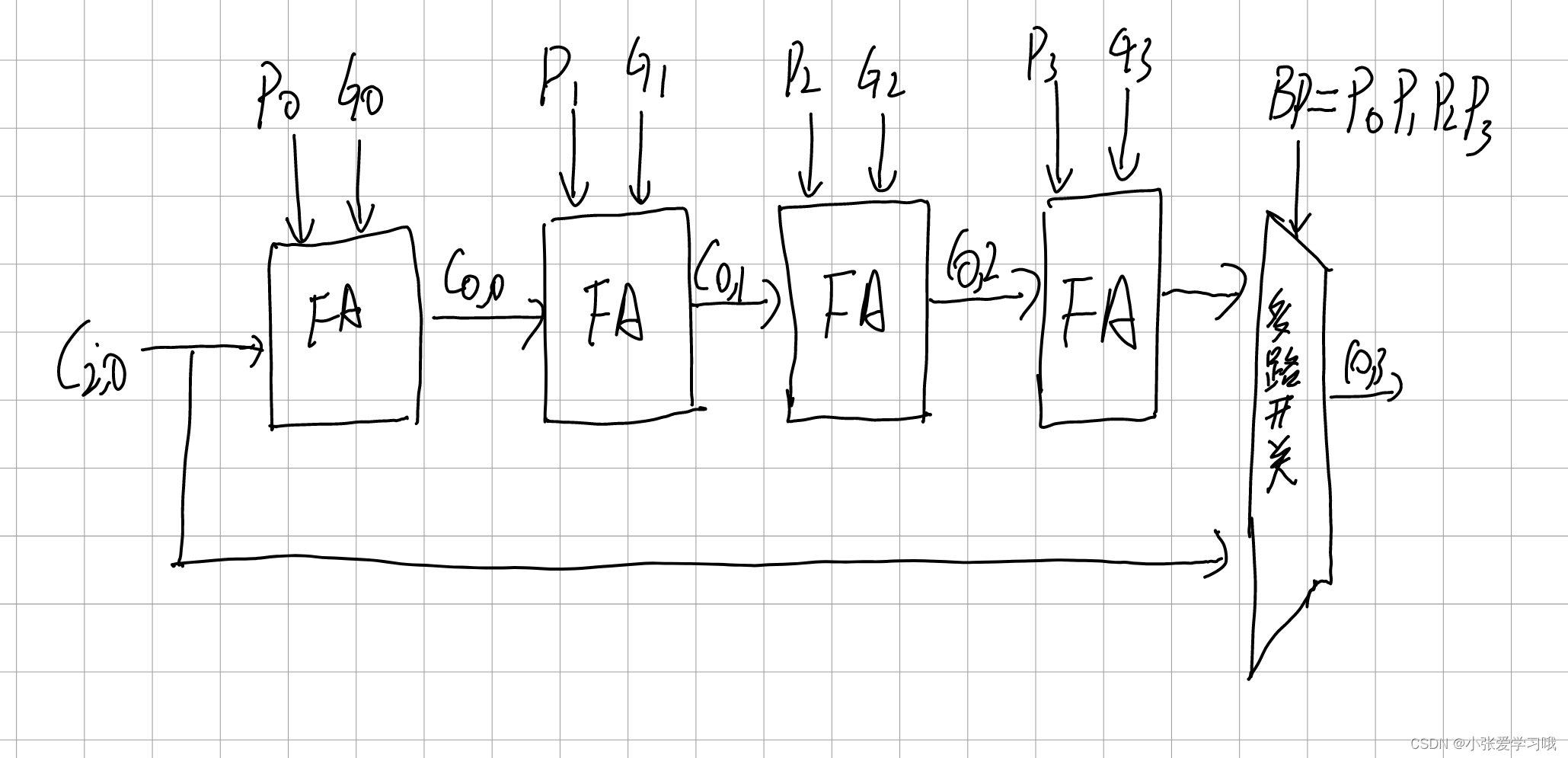
通过硬件描述实现四位全加器如下:
module adder_4bit(
input [3:0] A ,
input [3:0] B ,
input C , //地位进位信号
output [3:0] S,
output COUT //输入到高位的进位信号
);
//在基本加法器的基础上引入某些信号 :进位产生 进位取消 进位传播
//G(generate) : 进位产生信号:如果某一位加数a和加数b都是1则一定产生进位信号
//D(delete) : 进位取消信号:如果某一位加数a和加数b都是0则一定不产生进位信号
//P(propagate) : 进位传播信号:如果俩个加数不同,向高位的进位信号就与前一位的传递上来的进位信号有关了
//目前要设计的电路是旁路加法器
//每一位这些信号直接产生
wire [3:0]generat,delete,propagate;
wire [3:0]c_index;
wire DIRECT_PRA; //进位信号是否直接传输
assign generat[0]= A[0] & B[0];
assign generat[1]= A[1] & B[1];
assign generat[2]= A[2] & B[2];
assign generat[3]= A[3] & B[3];
//assign delete[0]= (~A[0]) & (~B[0]);
//assign delete[1]= (~A[1]) & (~B[1]);
//assign delete[2]= (~A[2]) & (~B[2]);
//assign delete[3]= (~A[3]) & (~B[3]);
assign propagate[0]= A[0] ^ B[0];
assign propagate[1]= A[1] ^ B[1];
assign propagate[2]= A[2] ^ B[2];
assign propagate[3]= A[3] ^ B[3];
//进位信号产生
assign c_index[0]= (generat[0]) | (propagate[0] & C);
assign c_index[1]= (generat[1]) | (propagate[1] & c_index[0]);
assign c_index[2]= (generat[2]) | (propagate[2] & c_index[1]);
assign c_index[3]= (generat[3]) | (propagate[3] & c_index[2]);
//进位信号是否直接传
assign DIRECT_PRA=propagate[0]&propagate[1]&propagate[2]&propagate[3];
//结果计算
assign S[0] = propagate[0] ^ C;
assign S[1] = propagate[1] ^ c_index[0];
assign S[2] = propagate[2] ^ c_index[1];
assign S[3] = propagate[3] ^ c_index[2];
assign COUT = (DIRECT_PRA)? C : c_index[3];
endmodule
简单对比以下四位旁路全加器和四位串行全加器:首先很容易理解四位串行全加器进位信号的最长路径为四个一位全加器的进位信号延时之和。那么分析以下旁路结构进位信号的最长路径,这里分析从多路开关的控制信号入手,当BP=1时(每一位的进位传播信号都是1),这时最高位的进位信号直接激素hi最低为的Ci。反之,若BP=0,则一定有某一位有进位产生或者消除,这时最坏的结果就是P0=0,P1=P2=P3=1,为最长路径,延时同样比串行结构短一些。(需要注意的是,对于P,BP的结果在输入给定的条件下其实就已经知道了。(这里我表述的可能不是很清楚,可以结合文字自己好好思考一下))。
四位旁路对应最长路径(红线):
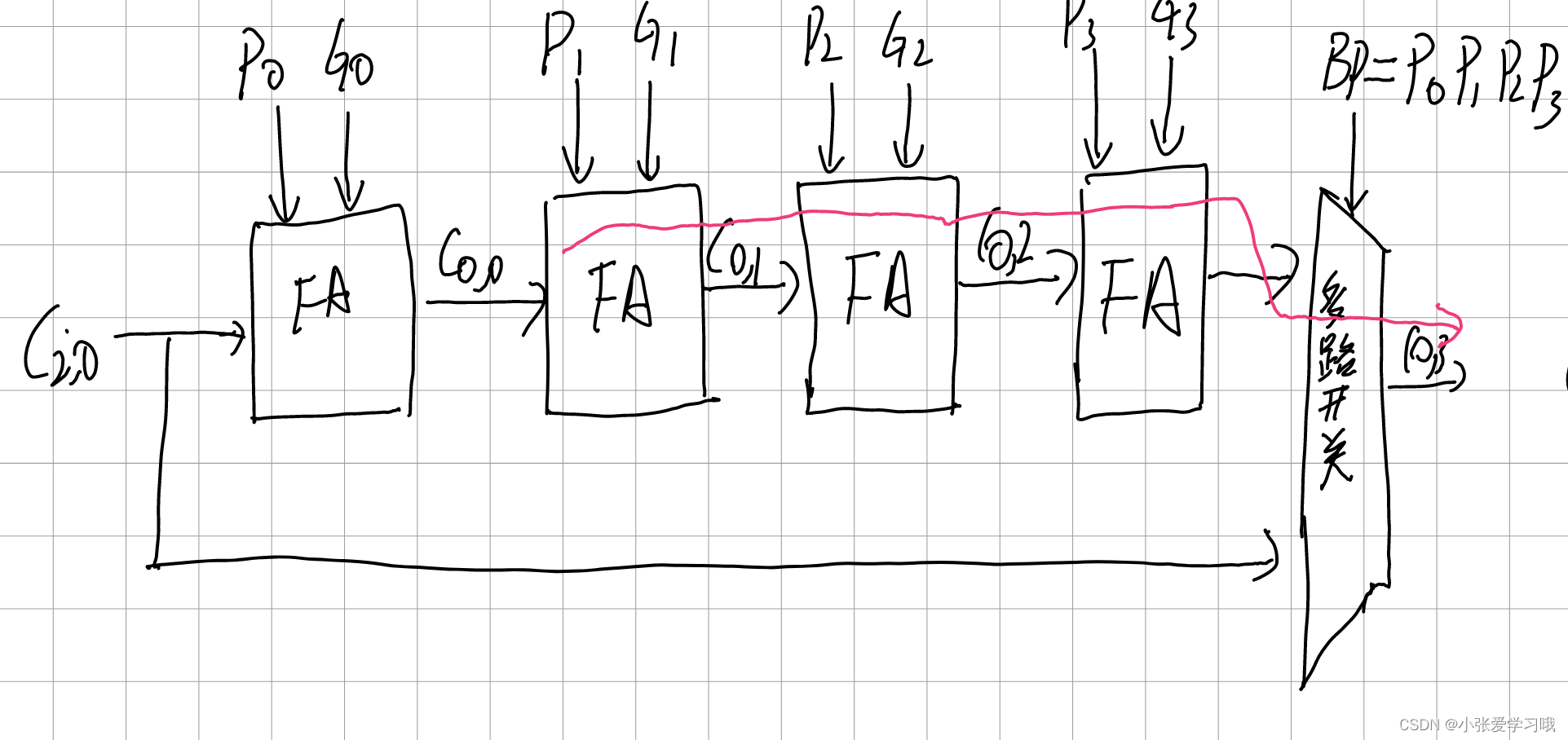
若将该结构继续扩展到8位则最长路径如下:
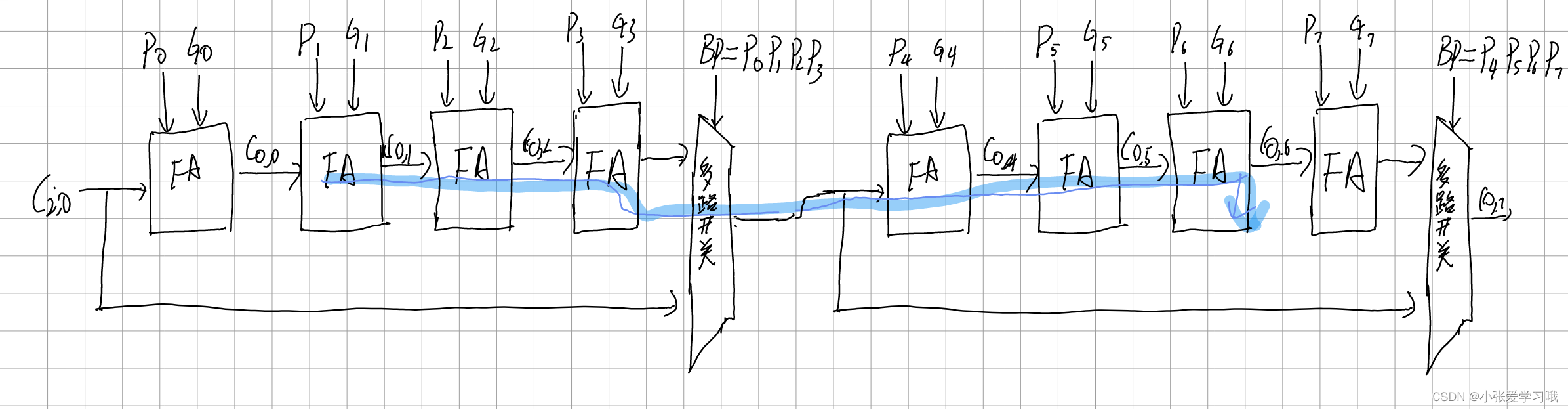
若继续拓展到12位则最长路径应该为:
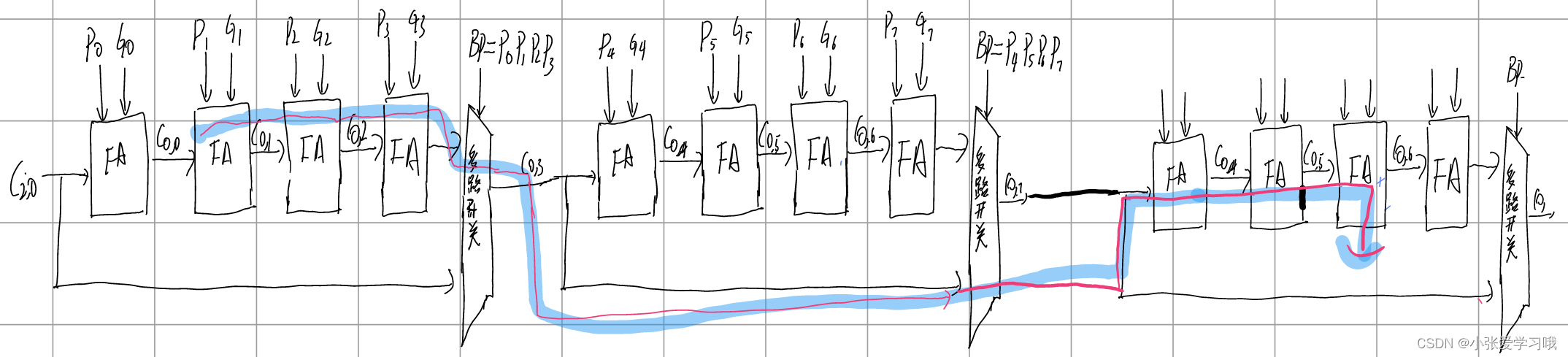
总结
总的来说当扩展的位数越多时,则优势就越大,但是带来的问题就是电路规模更大。在实际使用中要合理选择,选择最合适的电路。
本文大部分内容是在《数字集成电路》(周润德译)这本书所学,有兴趣可以在网上找电子版学习。
最后
以上就是任性黄豆最近收集整理的关于串行加法器和进位旁路加法器一位全加器8位串行加法器进位旁路加法器 总结的全部内容,更多相关串行加法器和进位旁路加法器一位全加器8位串行加法器进位旁路加法器 总结内容请搜索靠谱客的其他文章。








发表评论 取消回复