数学建模:现代优化算法之模拟退火
开始了开始了!!!
数学建模
- 数学建模:现代优化算法之模拟退火
- 前言
- Simulated annealing algorithm(SAA算法)
- 1.算法简介
- 数学基础
- 算法思路整理
- 补充:Metropolis算法
- 2.应用举例
- 参考
- 总结
肝!
前言
现代优化算法是上世纪80年代初兴起的启发式算法。这些算法包括禁忌搜索(tabu search),模拟退火(simulated annealing),遗传算法(genetic algorithms),人工神经网络(neural networks)。它们主要用于解决大量的实际应用问题。
目前,这些算法在理论和实际应用方面得到了较大的发展。无论这些算法是怎样产生的,它们有一个共同的目标——求NP-hard组合优化问题的全局最优解。虽然有这些目标,但NP-hard理论限制它们只能以启发式的算法去求解实际问题。
启发式算法包含的算法很多,例如解决复杂优化问题的蚁群算法(Ant Colony Algorithms)。有些启发式算法是根据实际问题而产生的,如解空间分解、解空间的限制等;另一类算法是集成算法,这些算法是诸多启发式算法的合成。
Simulated annealing algorithm(SAA算法)
1.算法简介
模拟退火算法得益于材料统计力学的研究成果。统计力学表明材料中粒子的不同结构对应于粒子的不同能量水平。在高温条件下,粒子的能量较高,可以自由运动和重新排列。在低温条件下,粒子能量较低。如果从高温开始,非常缓慢地降温(这个过程被称为退火),粒子就可以在每个温度下达到热平衡。当系统完全被冷却时,最终形成处于低能状态的晶体。
数学基础
如果用粒子的能量定义材料的状态,Metropolis算法用一个简单的数学模型描述了退火过程。假设材料在状态
i
i
i之下的能量为
E
(
i
)
E(i)
E(i),那么材料在温度
T
T
T时从状态
i
i
i进入状态
j
j
j就遵循如下规律:
(1)如果
E
(
j
)
≤
E
(
i
)
E(j)le E(i)
E(j)≤E(i),接受该状态被转换。
(2)如果
E
(
j
)
>
E
(
i
)
E(j)>E(i)
E(j)>E(i),则状态转换以如下概率被接受
e
E
(
i
)
−
E
(
j
)
K
T
,
e^frac{E(i)-E(j)}{KT},
eKTE(i)−E(j),
其中
K
K
K是物理学中的波尔兹曼常数,
T
T
T是材料温度。
在某一个特定温度下,进行了充分的转换之后,材料将达到热平衡。这时材料处于状态
i
i
i的概率满足波尔兹曼分布
P
T
(
X
=
i
)
=
e
−
E
(
i
)
K
T
∑
j
∈
S
e
−
E
(
j
)
K
T
,
P_T(X=i)=frac{e^{-frac{E(i)}{KT}}}{sum_{jin S} e^{-frac{E(j)}{KT}}},
PT(X=i)=∑j∈Se−KTE(j)e−KTE(i),
其中
X
X
X表示材料当前状态的随机变量,
S
S
S表示状态空间集合。
显然
lim
T
→
∞
e
−
E
(
i
)
K
T
∑
j
∈
S
e
−
E
(
j
)
K
T
=
1
∣
S
∣
,
lim_{Trightarrowinfty}{frac{e^{-frac{E(i)}{KT}}}{sum_{jin S} e^{-frac{E(j)}{KT}}}}=frac{1}{|S|},
T→∞lim∑j∈Se−KTE(j)e−KTE(i)=∣S∣1,
式中:
∣
S
∣
|S|
∣S∣表示集合S中状态的数量。这表明所有状态在高温下具有相同的概率。
而当温度下降时,有
lim
T
→
0
e
−
E
(
i
)
−
E
m
i
n
K
T
∑
j
∈
S
∑
e
−
E
(
j
)
−
E
m
i
n
K
T
=
lim
T
→
0
e
−
E
(
i
)
−
E
m
i
n
K
T
∑
j
∈
S
m
i
n
∑
+
∑
j
∉
S
m
i
n
∑
e
−
E
(
j
)
−
E
m
i
n
K
T
e
−
E
(
j
)
−
E
m
i
n
K
T
lim_{Trightarrow0}frac{e^{-frac{Eleft(iright)-E_{{min}}}{KT}}}{sum_{jin S}^{sum}e^{-frac{Eleft(jright)-E_{{min}}}{KT}}=lim_{Trightarrow0}frac{e^{-frac{Eleft(iright)-E_{{min}}}{KT}}}{sum_{jin S_{{min}}}^{sum+sum_{jnotin S_{{min}}}^{sum}e^{-frac{Eleft(jright)-E_{{min}}}{KT}}}e^{-frac{Eleft(jright)-E_{{min}}}{KT}}}}
T→0lim∑j∈S∑e−KTE(j)−Emin=limT→0∑j∈Smin∑+∑j∈/Smin∑e−KTE(j)−Emine−KTE(j)−Emine−KTE(i)−Emine−KTE(i)−Emin
式中:
E
min
j
∈
S
m
i
n
E
(
j
)
{Emin_{jin S}}_{min}{E(j)}
Eminj∈SminE(j)且
S
m
i
n
m
i
n
{S{min}}_{{min}}
Sminmin。
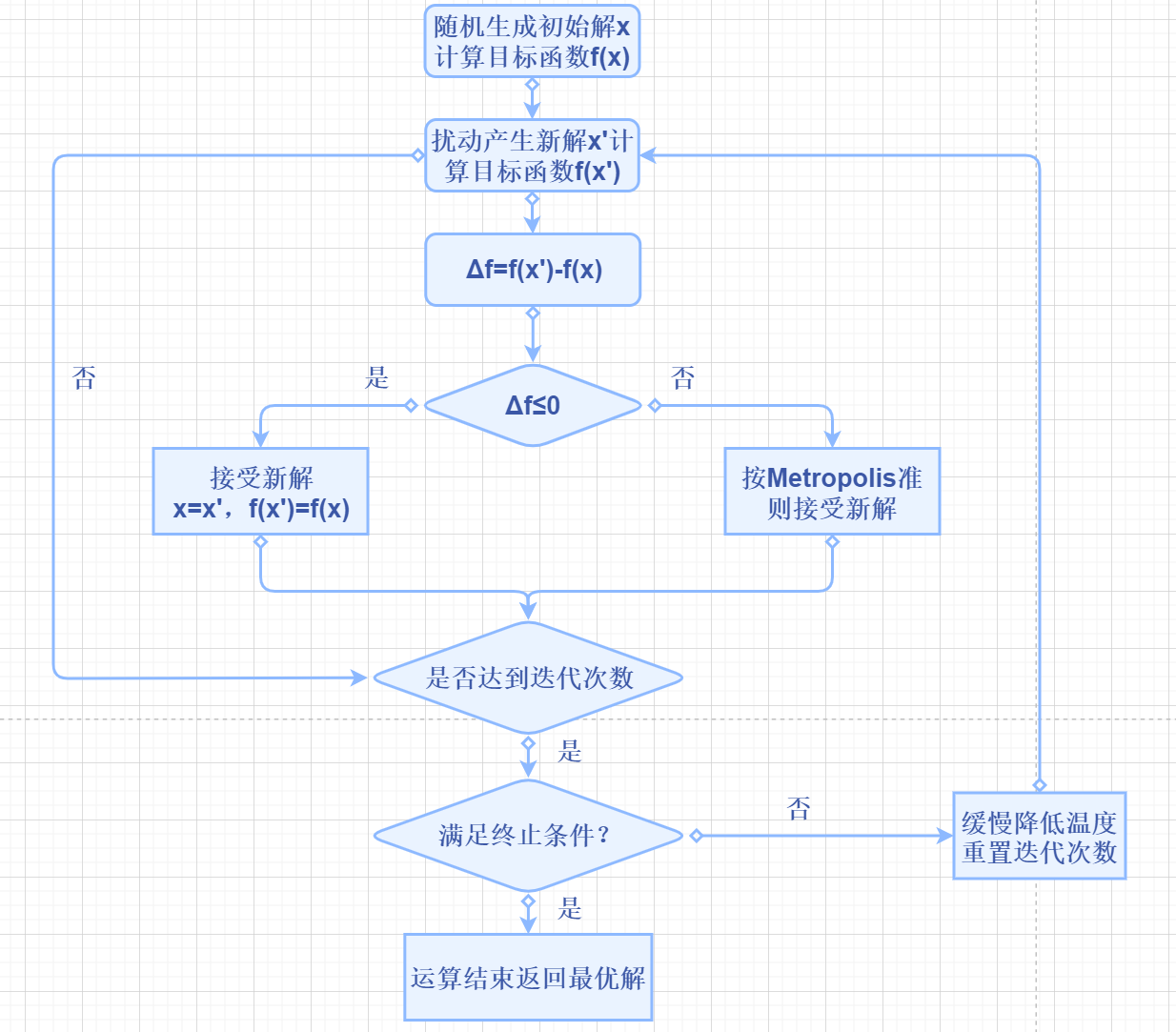
算法思路整理
算法流程
- 设定当前解(即为当前的最优解)
- 产生新解与当前解差值
- 判断新解是否被接受
- 当新解被确定接受时,新解被作为当前解
- 循环以上四个步骤
- 最后找到全局最优解
参数讲解
退火过程由一组初始参数,即冷却进度表控制。它的目的是尽量使系统达到平衡,以使算法在有限的时间内逼近最优解。
冷却进度表包括:
- 控制温度参数的初值 T 0 T_0 T0
- 控制温度 T T T的衰减参数(温度的更新)
- 马尔科夫链的长度 L k L_k Lk(迭代次数)
- 控制参数 T T T的终值(停止准则)
相似性比较
| 组合优化问题 | 金属物体 |
|---|---|
| 解 | 粒子状态 |
| 最优解 | 能量最低的状态 |
| 设定初温 | 熔解过程 |
| Methopolis | 等温过程 |
| 控制参数的下降 | 冷却 |
| 目标函数 | 能量 |
优点
· 高效地求解NP完全问题(如TSP问题,0-1背包问题等)
· 相较于其他非线性与优化算法,模拟退火算法编程工作量小且易于实现
缺点
· 使用不当,可能会陷入局部最优
· 参数难以控制,所得结果可能为接近最优解但并非最优解
算法对比



注意事项
(1)理论上,降温过程要足够缓慢,要使得在每一温度下达到热平衡。但在计算机实现中,如果降温速度过缓,所得到的解的性能会较为令人满意,但是算法会太慢,相对于简单的搜索算法不具有明显优势。如果降温速度过快,很可能最终得不到全局最优解。因此使用时要综合考虑解的性能和算法速度,在两者之间采取一种折衷。
(2)要确定在每一温度下状态转换的结束准则。实际操作可以考虑当连续 m m m次的转换过程没有使状态发生变化时结束该温度下的状态转换。最终温度的确定可以提前定为一个较小的值 T e T_e Te,或连续几个温度下转换过程没有使状态发生变化算法就结束。
(3)选择初始温度和确定某个可行解的邻域的方法也要恰当。
补充:Metropolis算法
Metropolis 算法是马尔可夫链蒙特卡洛【Markov Chain Monte Carlo, MCMC】的一种特殊算法。
Metropolis采样算法为CSDN博主「jingjishisi」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/jingjishisi/article/details/79291258
2.应用举例
【例一】 已知100个目标的经度、纬度如表12.1所示。
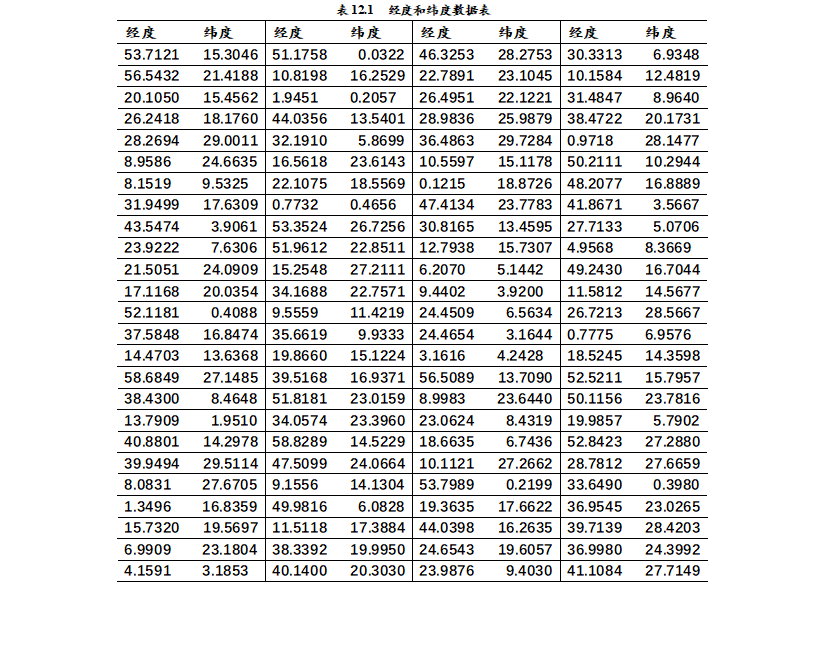
我方有一个基地,经度和纬度为
(
70
,
40
)
(70,40)
(70,40)。假设我方飞机的速度为
1000
1000
1000公里/小时。我方派一架飞机从基地出发,侦察完所有目标,再返回原来的基地。在每一目标点的侦察时间不计,求该架飞机所花费的时间(假设我方飞机巡航时间可以充分长)。
这是一个旅行商问题。给我方基地编号为 1 1 1,目标依次编号为 2 , 3 , … , 101 2,3,…,101 2,3,…,101,最后我方基地再重复编号为 102 102 102(这样便于程序中计算)。距离矩阵 D = ( d i j ) 102 × 102 D=(d_{ij})_{102times102} D=(dij)102×102,其中 d i j d_{ij} dij表示表示 i , j i,j i,j两点的距离, i , j = 1 , 2 , ⋯ , 102 i,j=1,2,cdots,102 i,j=1,2,⋯,102,这里 D D D为实对称矩阵。则问题是求一个从点 1 1 1出发,走遍所有中间点,到达点 102 102 102的一个最短路径。
上面问题中给定的是地理坐标(经度和纬度),必须求两点间的实际距离。设
A
,
B
A,B
A,B两点的地理坐标分别为
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
(x_1,y_1),(x_2,y_2)
(x1,y1),(x2,y2),过
A
,
B
A,B
A,B两点的大圆的劣弧长即为两点的实际距离。以地心为坐标原点
O
O
O,以赤道平面为
X
O
Y
XOY
XOY平面,以0度经线圈所在的平面为
X
O
Z
XOZ
XOZ平面建立三维直角坐标系。则
A
,
B
A,B
A,B两点的直角坐标分别为
A
(
R
cos
x
1
cos
y
1
,
R
sin
x
1
cos
y
1
,
R
sin
y
1
)
,
A(Rcos{x_1}cos{y_1},Rsin{x_1}cos{y_1},Rsin{y_1}),
A(Rcosx1cosy1,Rsinx1cosy1,Rsiny1),
B
(
R
cos
x
2
cos
y
2
,
R
sin
x
2
cos
y
2
,
R
sin
y
2
)
,
B(Rcos{x_2}cos{y_2},Rsin{x_2}cos{y_2},Rsin{y_2}),
B(Rcosx2cosy2,Rsinx2cosy2,Rsiny2),
式中:
R
=
6370
k
m
R=6370km
R=6370km为地球半径。
A
,
B
A,B
A,B两点的实际距离
d
=
R
a
r
c
c
o
s
(
O
A
⃗
⋅
O
B
⃗
∣
O
A
⃗
∣
⋅
∣
O
B
⃗
∣
)
,
d=R{arccos}{left(frac{vec{mathrm{OA}}cdotvec{OB}}{left|vec{mathrm{OA}}right|cdotleft|vec{OB}right|}right)},
d=Rarccos⎝⎛∣∣∣OA∣∣∣⋅∣∣∣OB∣∣∣OA⋅OB⎠⎞,
化简得
d
=
R
arccos
[
c
o
s
(
x
1
−
x
2
)
c
o
s
y
1
c
o
s
y
2
+
s
i
n
y
1
s
i
n
y
2
]
.
d=Rarccos{[}{cos}{(}x_1-x_2){cos}{y_1}{cos}{y_2}+{sin}{y_1}{sin}{y_2}].
d=Rarccos[cos(x1−x2)cosy1cosy2+siny1siny2].
推导过程如下:

求解的模拟退火算法描述如下:
(1)解空间
解空间
S
S
S可表为
1
,
2
,
⋯
,
101
,
102
{1,2,cdots,101,102}
1,2,⋯,101,102的所有固定起点和终点的循环排列集合,即
S
=
{
(
π
1
,
⋯
,
π
102
)
∣
π
1
=
1
,
(
π
2
,
⋯
,
π
101
)
为
2
,
3
,
⋯
,
101
的
循
环
排
列
,
π
102
=
102
}
,
S=lbrace{(pi_1,cdots,pi_{102})|pi_1=1,(pi_2,cdots,pi_{101})为{2,3,⋯,101}的循环排列,pi_{102}=102}rbrace ,
S={(π1,⋯,π102)∣π1=1,(π2,⋯,π101)为2,3,⋯,101的循环排列,π102=102},
其中每一个循环排列表示侦察
100
100
100个目标的一个回路,
π
i
=
j
pi_i=j
πi=j表示在第
i
−
1
i-1
i−1次侦察目标
j
j
j,初始解可选为
(
1
,
2
,
⋯
,
102
)
(1,2,cdots,102)
(1,2,⋯,102),本文中我们先使用Monte Carlo(蒙特卡洛)方法求得一个较好的初始解。
回顾蒙特卡洛方法:
线性规划问题中有所提及:
蒙特卡洛方法又称统计模拟法、随机抽样技术,是一种随机模拟方法,以概率和统计理论方法为基础的一种计算方法,是使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解。
(2)目标函数
目标函数(或称代价函数)为侦察所有目标的路径长度。要求
min
f
(
π
1
,
π
2
,
⋯
,
π
102
)
=
∑
i
=
1
101
d
π
i
π
i
+
1
,
min{f}(pi_1,pi_2,cdots,pi_{102})=sum_{i=1}^{101}d_{pi_ipi_{i+1}},
minf(π1,π2,⋯,π102)=i=1∑101dπiπi+1,
而一次迭代由下列三步构成
(3)新解的产生
设上一步迭代的解为
π
1
⋯
π
u
−
1
π
u
π
u
+
1
⋯
π
v
−
1
π
v
π
v
+
1
⋯
π
w
−
1
π
w
π
w
+
1
⋯
π
102
。
pi_1cdotspi_{u-1}pi_upi_{u+1}cdotspi_{v-1}pi_vpi_{v+1}cdotspi_{w-1}pi_wpi_{w+1}cdotspi_{102}。
π1⋯πu−1πuπu+1⋯πv−1πvπv+1⋯πw−1πwπw+1⋯π102。
i) 2变换法
任选序号 u , v u,v u,v,交换 u u u与 v v v之间的顺序,变成逆序,此时的新路径为
π 1 ⋯ π u − 1 π v π v − 1 ⋯ π u + 1 π u π v + 1 ⋯ π 102 . pi_1cdotspi_{u-1}pi_vpi_{v-1}cdotspi_{u+1}pi_upi_{v+1}cdotspi_{102}. π1⋯πu−1πvπv−1⋯πu+1πuπv+1⋯π102.ii) 3变换法
任选序号 u , v u,v u,v和 w w w,将 u u u和 v v v之间的路径插到 w w w之后,对应的新路径为
π 1 ⋯ π u − 1 π v + 1 ⋯ π w π u ⋯ π v π w + 1 ⋯ π 102 pi_1cdotspi_{u-1}pi_{v+1}cdotspi_wpi_ucdotspi_vpi_{w+1}cdotspi_{102} π1⋯πu−1πv+1⋯πwπu⋯πvπw+1⋯π102
(4)代价函数差
对于2变换法,路径差可表示为
Δ
f
=
(
d
π
u
−
1
π
v
+
d
π
u
π
v
+
1
)
−
(
d
π
u
−
1
π
u
+
d
π
v
π
v
+
1
)
Delta f=(d_{pi_{u-1}pi_v}+d_{pi_upi_{v+1}})-(d_{pi_{u-1}pi_u}+d_{pi_vpi_{v+1}})
Δf=(dπu−1πv+dπuπv+1)−(dπu−1πu+dπvπv+1)
(5)接受准则
P = { 1 , Δ f < 0 , e x p ( − Δ f / T ) , Δ f ≥ 0. P=begin{cases} 1,&Δf<0,\ exp(-Δf/T),&Δf≥0.\ end{cases} P={1,exp(−Δf/T),Δf<0,Δf≥0.
如果 Δ f < 0 Delta f<0 Δf<0,则接受新的路径。否则,以概率 e x p ( − Δ f / T ) {exp}{(}-Delta f/T) exp(−Δf/T) 接受新的路径,即用计算机产生一个[0,1]区间上均匀分布的随机数rand,若 r a n d ≤ e x p ( − Δ f / T ) randle{exp}{(}-Delta f/T) rand≤exp(−Δf/T)则接受。
(6)降温
利用选定的降温系数 α alpha α进行降温,取新的温度 T T T为 α T alpha T αT(这里 T T T为上一步迭代的温度),这里选定 α = 0.999 alpha=0.999 α=0.999。
(7)结束条件
用选定的终止温度 e = 1 0 − 30 e=10^{-30} e=10−30,判断退火过程是否结束。若 T < e T<e T<e,算法结束,输出当前状态。
编写MATLAB程序如下:
clc, clear, close all
%% 数据预处理
sj0=load('C:UsersAdministratorDesktop“高教杯”国赛备赛数学建模算法与应用(第3版)源程序程序及数据12第12章 现代优化算法data12_1.txt');
x=sj0(:,[1:2:8]); x=x(:); %取奇数列(经度列)
y=sj0(:,[2:2:8]); y=y(:); %取偶数列(维度列)
sj=[x y] %【经度,维度】
d1=[70,40]; %基地位置,经度和纬度为(70,40)
xy=[d1;sj;d1]; %将基地位置加在首尾
%% 目标函数
sj=xy*pi/180; %角度化成弧度
d=zeros(102); %距离矩阵d初始化
%计算弧长
for i=1:101
for j=i+1:102
d(i,j)=6370*acos(cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*...
cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)));
end
end
d=d+d';
%% 初始解
path=[];long=inf; %巡航路径及长度初始化 设置long为无穷大
for j=1:1000 %求较好的初始解
path0=[1 1+randperm(100),102]; temp=0; % p = randperm(n)生成一个从 1 到 n 的整数的随机排列
for i=1:101
temp=temp+d(path0(i),path0(i+1));
end
if temp<long
path=path0; long=temp;
end
end
%% 导入参数
e=0.1^30; % 控制温度参数的终值
L=20000; % 马尔科夫链的长度
at=0.999; % 控制温度的损减参数
T=1; % 控制温度参数的初值
%% 退火过程
for k=1:L
% 新解的产生
c=2+floor(100*rand(1,2)); % floor():朝负无穷大四舍五入,相当于"下取整"
c=sort(c); c1=c(1);c2=c(2); % c1最小,c2次小
%计算代价函数值的增量
df=d(path(c1-1),path(c2))+d(path(c1),path(c2+1))-...
d(path(c1-1),path(c1))-d(path(c2),path(c2+1));
%接受准则
if df<0 %接受,则状态转换
path=[path(1:c1-1),path(c2:-1:c1),path(c2+1:102)]; long=long+df;
elseif exp(-df/T)>=rand %否则则以一定的概率接受
path=[path(1:c1-1),path(c2:-1:c1),path(c2+1:102)]; long=long+df;
end
%降温
T=T*at;
if T<e
break;
end
end
%% 输出结果
path, long % 输出巡航路径及路径长度
xx=xy(path,1); yy=xy(path,2);
%% 可视化
plot(xx,yy,'-*') %画出巡航路径
计算结果为44小时左右。其中的一个巡航路径如图12.1所示。
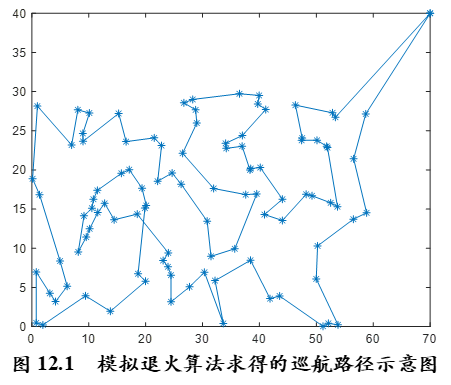
参考
1,《数学建模算法及其应用》第五版
2, 感谢哔哩哔哩up主:连大数学建模
参考网址2021美赛赛前培训
总结
keep going on!
最后
以上就是活泼金毛最近收集整理的关于数学建模:现代优化算法之模拟退火数学建模:现代优化算法之模拟退火前言Simulated annealing algorithm(SAA算法)参考总结的全部内容,更多相关数学建模:现代优化算法之模拟退火数学建模:现代优化算法之模拟退火前言Simulated内容请搜索靠谱客的其他文章。








发表评论 取消回复