使用java实现一维FFT傅里叶变换基础FFT

77 阅读 0 评论 51 点赞

我是靠谱客的博主土豪画板，最近开发中收集的这篇文章主要介绍使用java实现一维FFT傅里叶变换基础FFT，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

傅里叶变换基础

FFT是快速傅里叶变换，它是DFT的快速算法，但是计算结果与DFT等价。首先回顾一下傅里叶变换的计算公式：

首先，非周期性连续时间信号x(t)的傅里叶变换可以表示为：（公式1）
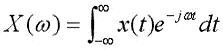
在这里插入图片描述

在离散的情况下，傅里叶变换的公式为：（公式2）
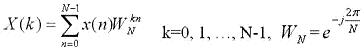
在这里插入图片描述
上面就是DFT的计算公式。DFT用代码实现是很简单的，因为，对于任意指定数值的K，只需要遍历N个采样点即可得到该K值下的频谱。不过DFT的复杂度为O(N^2)，在N较大的情况下，计算速度是很慢的。

FFT

FFT本身是DFT的变体，所以我们需要先了解DFT的理论。下面先简单介绍FFT的原理：
还是对x(n)信号求傅里叶变换。x(n)本身可以拆分成下标为奇数子集和偶数子集。
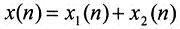
在这里插入图片描述

x1(n)和x2(n)的长度都是N／2，x1(n)是偶数序列，x2(n)是奇数序列，则：（公式3）
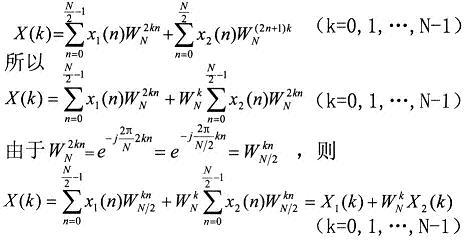
在这里插入图片描述
其中X1(k)和X2(k)分别为x1(n)和x2(n)的N／2点DFT。由于X1(k)和X2(k)均以N／2为周期，且WN k+N/2=-WN k，所以X(k)又可表示为：（公式4）

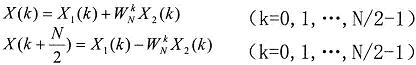
写到这里就不难发现，FFT本质上是采用分治算法来计算的DFT。一个初始长度为N的初始数据，最后会被分治为很多长度为2 的数据，然后分别对这些长度为2的数据做DFT，最终等价于对整个N长度的数据做傅里叶变换。
分治其实是一种思想，具体的实现其实就是使用递归。在写Java程序之前，我们需要做一些准备工作。FFT的运算过程中涉及到复数的运算。公式4中包含了复数的加法和乘法。因此我们在Java程序中需要建立一个Complex（复数）类，除了real（实部）和imag（虚部）两个属性以外，需要给Complex类定义add方法和multiply方法。这样的话，Complex类不仅仅可以用作复数对象存储实部和虚部，还能实现复数的运算。Java中不能实现运算符的重载，这是挺遗憾的事情，这样的话就不能直接用加减乘除号来进行Complex对象之间的运算了。
以下是Complex类的定义：

// Struct to hold two primary type
public static class Complex2 {
public double real;
public double imag;
Complex2() {
this.real = 0;
this.imag = 0;
}
Complex2(double real, double imag) {
this.real = real;
this.imag = imag;
}
Complex2 add(Complex2 another) {
return new Complex2(this.real + another.real, this.imag + another.imag);
}
Complex2 scalarMultiply(Complex2 another) {
double x1 = this.real;
double x2 = another.real;
double y1 = this.imag;
double y2 = another.imag;
return new Complex2(x1*x2-y1*y2, x1*y2+x2*y1);
}
}

复数的加法是实部加实部，虚部加虚部。复数的乘法是类似于多项式相乘。正如代码所示。
下面进入正题。实现FFT主函数。FFT主函数必须分成两个函数来写，因为其中一个是递归函数，需要分离出来才能做递归。代码如下：

public static Complex2[] fft(List<Double> dataList) {
// Get the size of dataList
final int N = dataList.size();
Complex2[] fftResult = new Complex2[N];
// Traverse dataList by index k from 0 to size of dataList
for(int k=0 ; k<N ; k++) {
fftResult[k] = fftRecursion(dataList, N, k);
}
return fftResult;
}

这是fft的主函数，主函数中主要是做了一个循环，因为我们需要求K频域上K从0~N-1变化过程中的频谱。对于每一个不同的K值，我们分别调用fftRecursion函数来实现分治算法。下面列出fftRecursion函数的实现：

/**
* Realize FFT by divide-and-conquer algorithm
*
* @param ALineUnit This is List of fragemnt of ALine Points. The termination of recursion
*
is sometime when size of ALineUnit is 2
*/
private static Complex2 fftRecursion(List<Double> ALineUnit, int unitLength, int k) {
if(unitLength == 2) {
Complex2 unit2 = new Complex2();
// Apply FFT to data list (size:2)
double xn;
// Get real value
for(int k1=0 ; k1<2 ; k1++) {
for(int n=0 ; n<2 ; n++) {
xn = ALineUnit.get(n);
unit2.real += xn * cos(2*PI*k1*n/2);
unit2.imag -= xn * sin(2*PI*k1*n/2);
}
}
return unit2;
}
else {
// Cut odd and even component of the current unit
List<Double> oddList = new ArrayList<>();
List<Double> evenList = new ArrayList<>();
for(int i=0 ; i<unitLength/2 ; i++) {
oddList.add(ALineUnit.get(2*i + 1));
evenList.add(ALineUnit.get(2*i));
}
return fftRecursion(evenList, unitLength/2, k).add(new Complex2(cos(2*PI*k/unitLength), -sin(2*PI*k/unitLength)).scalarMultiply(fftRecursion(oddList, unitLength/2, k)));
}
}

需要给递归设置一个终止递归的条件。也就是说当递归进行到每个数据包的长度已经变成2的时候，就可以对每个数据包做DFT，最后整体实现一个FFT的效果。
在递归还没有进行到数据包长度等于2之前，我们需要依照公式4的第一个公式对当前的数据包进行拆分，拆成奇数项和偶数项，然后对照公式4中的第一个公式，把k代进去（k在递归的过程中是个常数），同时做复数的加法和乘法（这个是我们在Complex类中就已经实现了的）。
以上。