Author:AXYZdong 自动化专业 工科男
有一点思考,有一点想法,有一点理性!
定个小小目标,努力成为习惯!在最美的年华遇见更好的自己!
CSDN@AXYZdong,CSDN首发,AXYZdong原创
唯一博客更新的地址为: ???? AXYZdong的博客 ????
B站主页为:AXYZdong的个人主页
零阶保持器(ZOH)频率特性分析
零阶保持器传递函数:
G ( s ) = 1 − e − T s s G(s)=frac{1-e^{-Ts}}{s} G(s)=s1−e−Ts
画 Bode 图进行频率分析:
s=tf('s');
T=0.1; %采样周期0.1s
G=(1-exp(-T*s))/s;
bode(G);
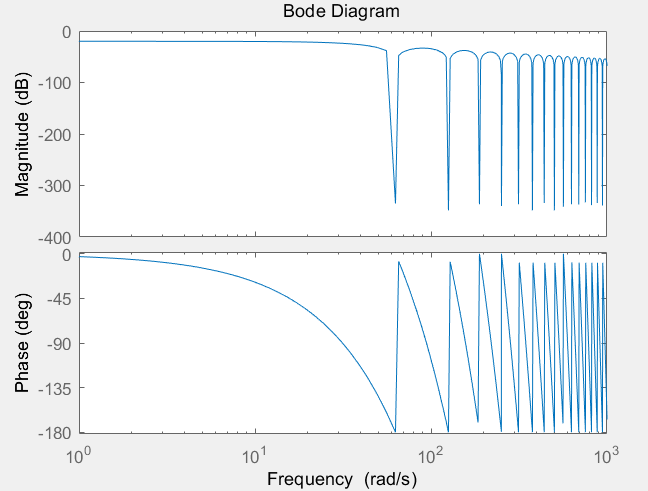
▲ 零阶保持器幅相特性
从图中可以看出:随着频率 ω omega ω 的的增加,当 ω omega ω 在 1 0 2 10^2 102 附近时,零阶保持器的幅值和相位开始发生跳变。
- 幅频特性中,幅值达到最低时立即发生跳变至最高,保持稳定后再次跳变至最低,如此往复;
- 相频特性中,相位滞后,在 − 18 0 。 − 0 。 -180^。- 0^。 −180。−0。 之间呈锯齿状变化;
- 从图中可以看出,零阶保持器是一个低通滤波器,但不是一个理想低通滤波器,高频信号通过零阶保持器不能完全消除,同时产生相位滞后。
一阶保持器(FOH)频率特性分析
一阶保持器传递函数:
G ( s ) = T ( 1 + T s ) ( 1 − e − T s T s ) 2 G(s)=T(1+Ts) left(frac{1-e^{-Ts}}{Ts}right)^2 G(s)=T(1+Ts)(Ts1−e−Ts)2
画 Bode 图进行频率分析:
s=tf('s');
T=0.1; %采样周期0.1s
G=T*(1+T*s)*((1-exp(-s*T))/(T*s))^2;
bode(G);
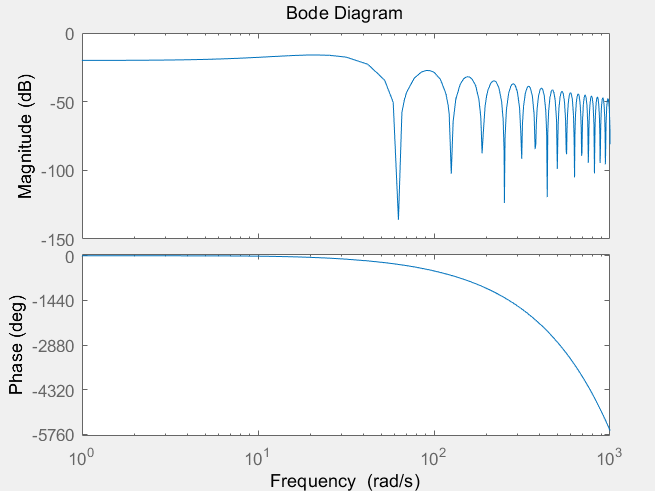
▲ 一阶保持器幅相特性
从图中可以看出:随着频率 ω omega ω 的的增加,当 ω omega ω 在 1 0 2 10^2 102 附近时,一阶保持器的幅值开始发生跳变。
- 幅频特性中,幅值达到最低时立即发生跳变至最高,与零阶保持器相比,变化更快;
- 相频特性中,相位大小一直增加,相位滞后更加严重。
如果我的博客对你有帮助、如果你喜欢我的博客内容,请 “点赞” “评论” “收藏” 一键三连哦!
听说 ???? 点赞 ???? 的人运气不会太差,每一天都会元气满满呦!^ _ ^ ❤️ ❤️ ❤️
如果以上内容有任何错误或者不准确的地方,欢迎在下面 ???? 留个言。或者你有更好的想法,欢迎一起交流学习~~~
最后
以上就是危机咖啡豆最近收集整理的关于「计算机控制技术」零阶保持器和一阶保持器的频率特性分析的全部内容,更多相关「计算机控制技术」零阶保持器和一阶保持器内容请搜索靠谱客的其他文章。








发表评论 取消回复