代码

构造函数

function [yn,xn] = RKorder4(f,a,b,h,y0)
%a，b为上下界；h为步长；y0为初值。
%返回yn、xn向量，并绘制曲线
yn=zeros(1,((b-a)/h)+1);
yn(1)=y0;
xn=a:h:b;
for i=1:((b-a)/h)
k1=h*f(xn(i),yn(i));
k2=h*f(xn(i)+h/2,yn(i)+k1/2);
k3=h*f(xn(i)+h/2,yn(i)+k2/2);
k4=h*f(xn(i)+h,yn(i)+k3);
yn(i+1)=yn(i)+(1/6)*(k1+2*k2+2*k3+k4);
end
end

实例

对于某暂态电路的初值问题：
$$\{\begin{array}{c}\frac{\mathrm{d}i}{\mathrm{d}t}=622sin314t-20i\\ i(0)=0\end{array}$$
$f(t_n,i_n)=622sin314t-20i$
取h=0.001，在[0,0.01]的时间区间内求解微分方程，得出电流值。
在命令窗口输入

a=0;b=0.01;h=0.001；
y0=0;
f=@(t,i) 622*sin(314*t)-20*i;
[yn,xn] = RKorder4(f,a,b,h,y0);
plot(xn,yn);grid on

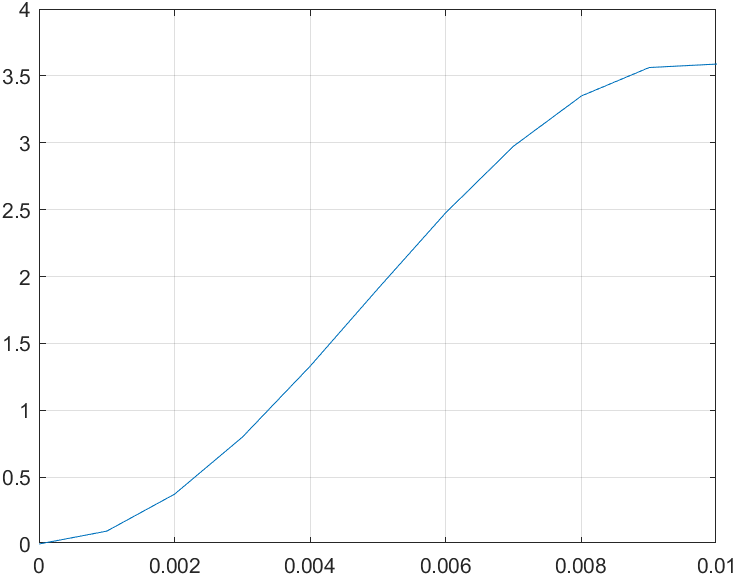
又由暂态电路理论分析得，此电路的解析解为：
$$i(t)=\frac{48827}{24749}\left(e^{-20t}+\frac{10}{157}sin314t-cos314t\right)$$
输入命令，将解析解和数值解的曲线绘制在同一图内：

i=@(t) (48827/24749).*(exp(-20.*t)+(10/157)*sin(314.*t)-cos(314.*t));
plot(linspace(0,0.01,1000),i(linspace(0,0.01,1000)),'r',xn,yn,'b');grid on

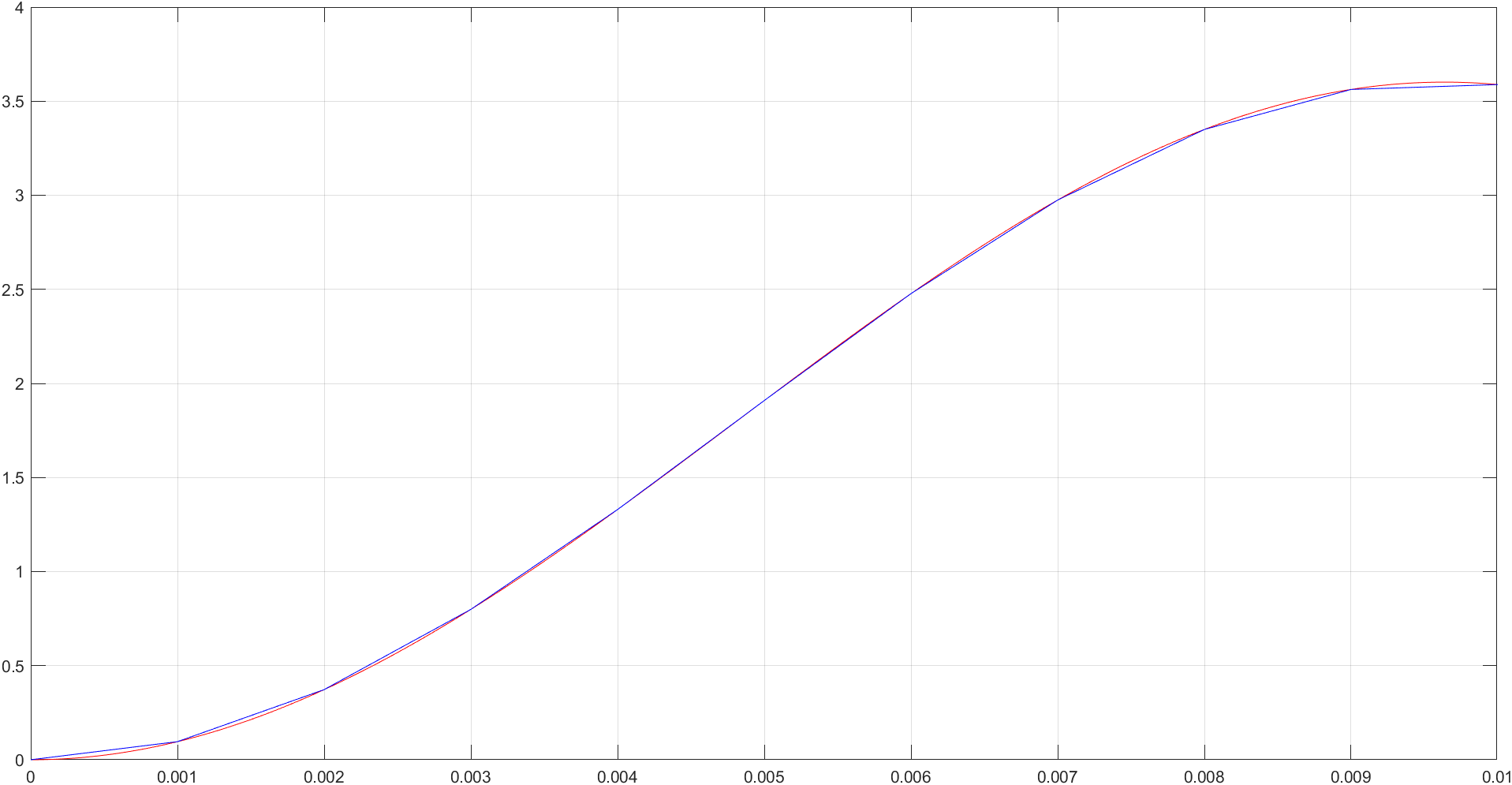
最后

以上就是烂漫鸡为你收集整理的基于MATLAB实现固定步长的四阶龙格库塔方法求解常微分方程初值问题代码实例的全部内容，希望文章能够帮你解决基于MATLAB实现固定步长的四阶龙格库塔方法求解常微分方程初值问题代码实例所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。