我是靠谱客的博主 慈祥小伙,这篇文章主要介绍基于MATLAB的微分方程的定步长与动步长算法对比解法(附完整代码)一. 四阶定步长Runge-Kutta算法 二. 四阶五级Runge-Kutta-Felhberg算法三. 微分方程求解函数,现在分享给大家,希望可以做个参考。
目录
一. 四阶定步长Runge-Kutta算法
二. 四阶五级Runge-Kutta-Felhberg算法
三. 微分方程求解函数
3.1 求解格式
3.2 描述微分方程组
例题1
例题2
一. 四阶定步长Runge-Kutta算法
令h代表计算步长,该算法的主题思想如下:
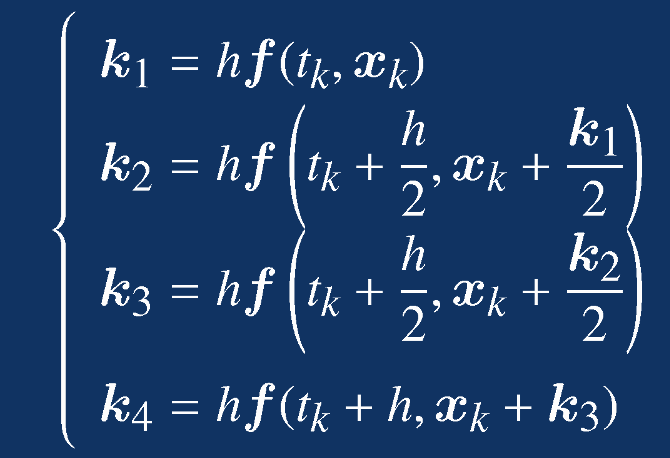
下一个步长的状态变量值,可计算如下:
形成MATLAB代码如下:
function [tout,yout]=rk_4(odefile,tspan,y0) %y0初值列向量
t0=tspan(1);
th=tspan(2);
if length(tspan)<=3,h=tspan(3); %tspan=[t0,th,h]
else h=tspan(2)-tspan(1);
th=tspan(end);
end %等间距的数组
tout=[t0;h;th]';
yout=[];
for t=tout'
k1=h*eval([odefile'(t,y0)']); %odefile是一个字符串变量,为表示微分方程f()的文件名
k2=h*eval([odefile'(t+h/2,y0+0.5*k1)']);
k3=h*eval([odefile'(t+h/2,y0+0.5*k2)']);
k4=h*eval([odefile'(t+h,y0+k3)']);
y0=y0+(k1+2*k2+2*k3+k4)/6;
yout=[yout;y0'];
end
end
%实际上该算法不是一个较好的方法二. 四阶五级Runge-Kutta-Felhberg算法
假设当前的步长为,定义6个
变量,如下:
下一步的状态向量可计算如下:
定义一个误差向量,如下:
通过误差向量调节步长,这个过程就被称之为自动变步长方法。实际上,四阶五级RKF算法有自己的参量系数表。
三. 微分方程求解函数
3.1 求解格式
利用ode45()函数,主要由三种格式。
格式1:直接求解
[t,x]=ode45(Fun,[t0,tf],x0)格式2:带有控制参数
[t,x]=ode45(Fun,[t0,tf],x0,options)格式3:带有附加参数
[t,x]=ode45(Fun,[t0,tf],x0,options,p1,p2,···)以上格式中[t0,tf]代表求解区间,x0代表初值问题的初始状态变量。
3.2 描述微分方程组
如果不附加变量,格式如下:
function xd=funname(t,x)也可以附加变量,格式如下:
function xd=funname(t,x,flag,p1,p2,···)
%t是时间变量或者是自变量,是必须要给的
%x为状态向量
%xd为返回状态向量的导数
%flag用来控制求解过程,指定初值,即使初值不用指定,也必须要有该变量占位
options是唯一结构体变量,可以用odeset()修改。
%格式1
options=odeset('RelTol',1e-7)
%格式2
options=odeset;
options.RelTol=1e-7;例题1
求解Lorenz模型的状态方程。
参数值如下:
初值如下:
微分模型如下:
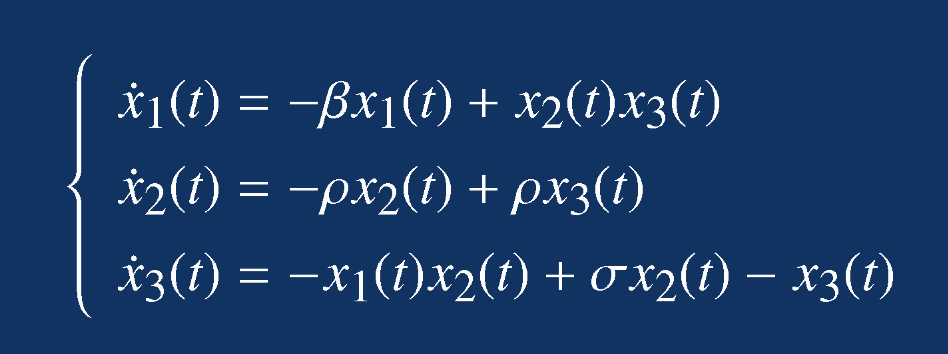
解:
此题代码由两个部分组成
(1)原方程文件
function xdot=lorenzeq(t,x)
xdot=[-8/3*x(1)+x(2)*x(3);-10*x(2)+10*x(3);-x(1)*x(2)+28*x(2)-x(3)];(2)主运行文件
clc;clear;
t_final=100;
x0=[0;0;1e-10]; %t_final为设定的仿真终止时间
[t,x]=ode45('lorenzeq',[0,t_final],x0);
plot(t,x)
figure; %打开新图形窗口
plot3(x(:,1),x(:,2),x(:,3));
axis([5 50 -25 25 -25 30]); %根据实际数值手动设置坐标系
figure;
comet3(x(:,1),x(:,2),x(:,3)) %绘制动画式的轨迹
运行结果:
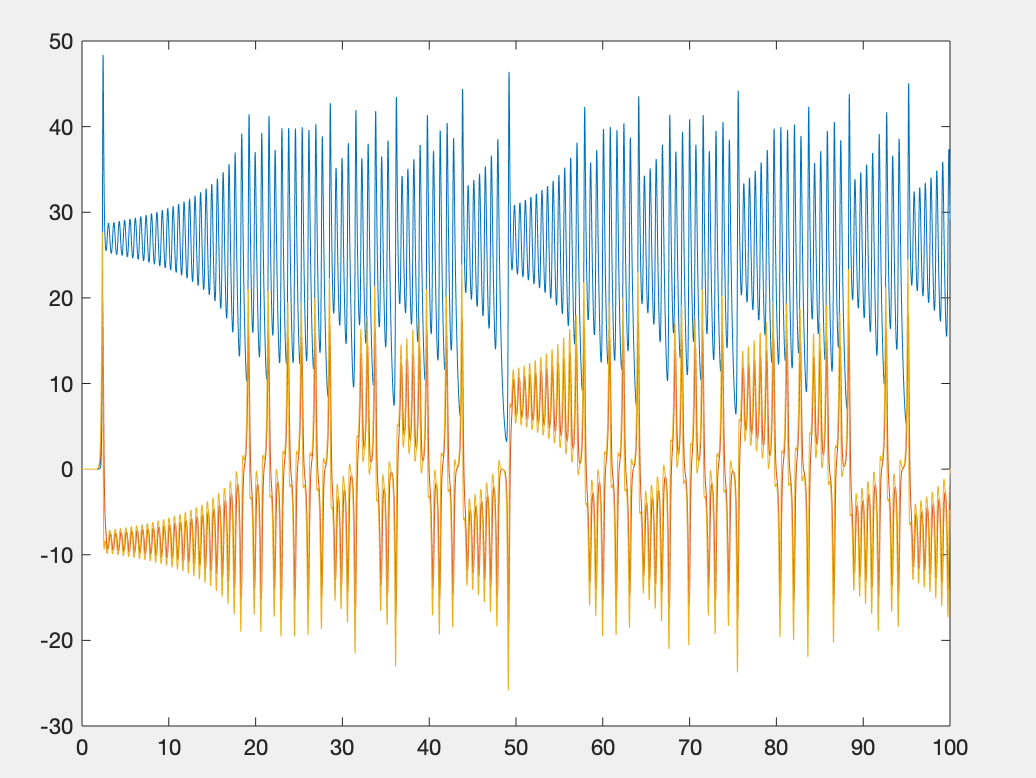
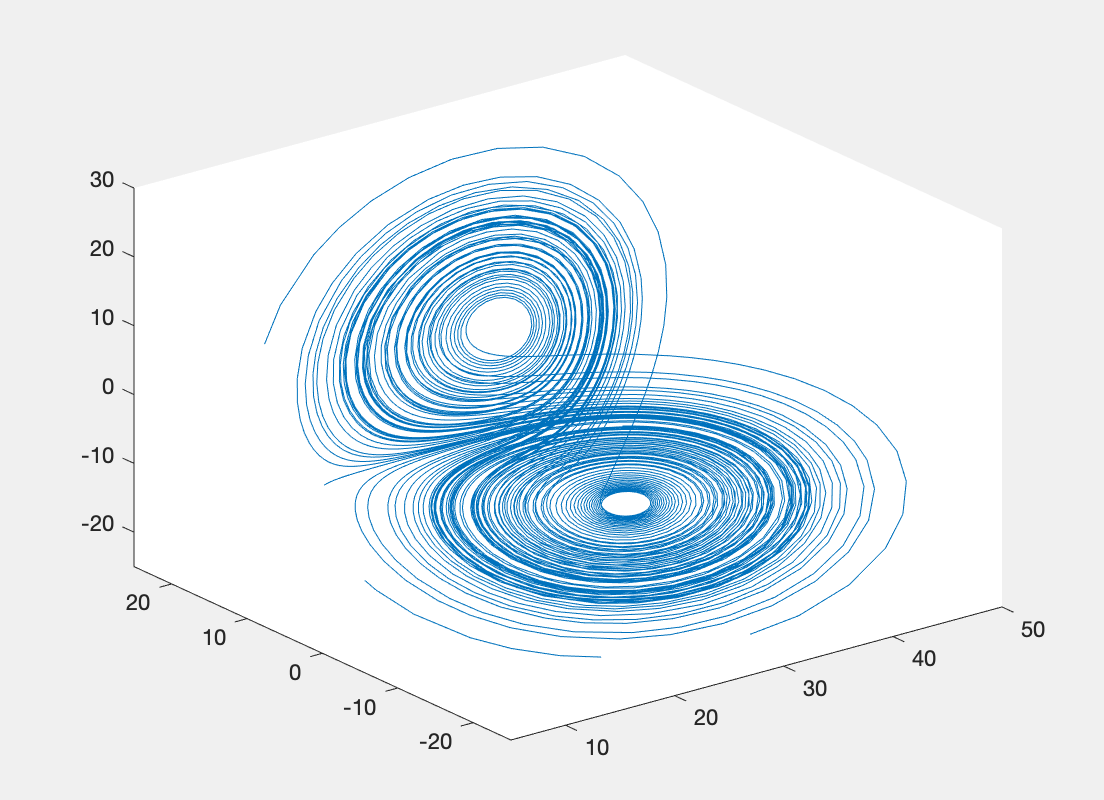
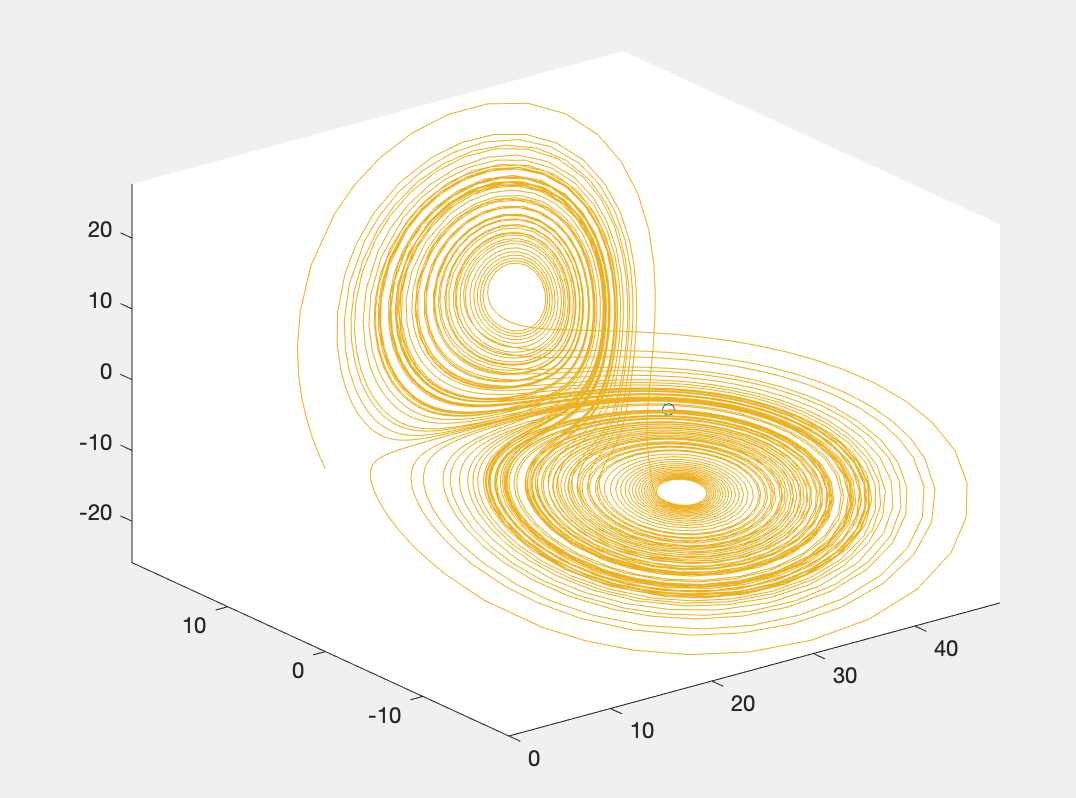
备注:图3实际上是一个动画的形式
例题2
带有附加参数的微分方程求解:洛伦茨方程。
编写有附加参数的函数描述Lorenz方程。
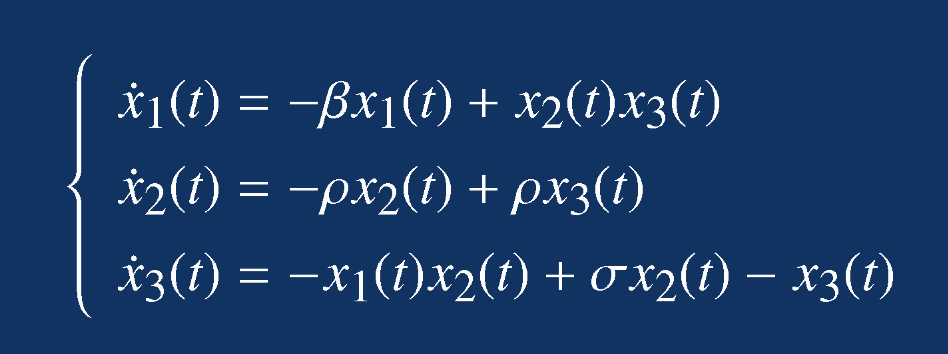
求解一组参数下,方程的数值解。
解:
此题有两个代码文件。
(1)原微分方程文件
function xdot=lorenz1(t,x,flag,beta,rho,sigma) %flag变量是不能省略的
xdot=[-beta*x(1)+x(2)*x(3);-rho*x(2)+rho*x(3);-x(1)*x(2)+sigma*x(2)-x(3)];(2)主运行文件
clc;clear;
%求微分方程
t_final=100;
x0=[0;0;1e-10];
b2=2;r2=5;s2=20;
[t2,x2]=ode45('lorenz1',[0,t_final],x0,[],b2,r2,s2);
%options位置为[],表示不需要修改控制项
plot(t2,x2)
figure;
plot3(x2(:,1),x2(:,2),x2(:,3));
axis([0 72 -20 22 -35 40]);运行结果:

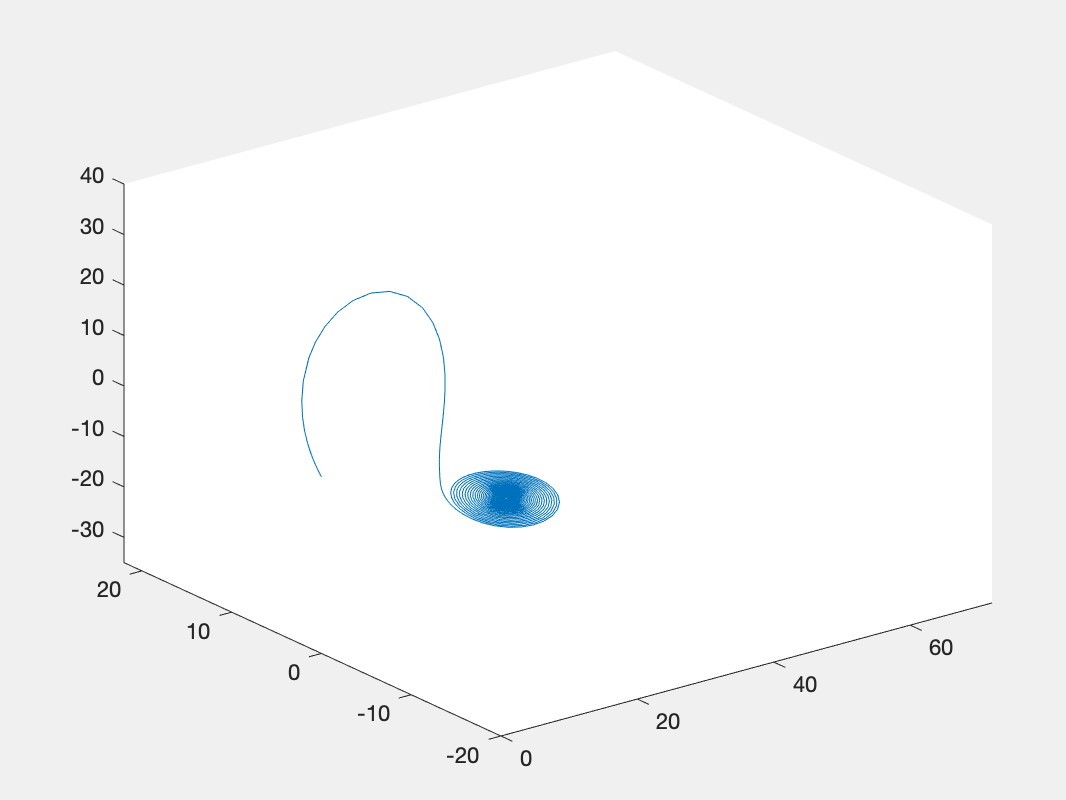
最后
以上就是慈祥小伙最近收集整理的关于基于MATLAB的微分方程的定步长与动步长算法对比解法(附完整代码)一. 四阶定步长Runge-Kutta算法 二. 四阶五级Runge-Kutta-Felhberg算法三. 微分方程求解函数的全部内容,更多相关基于MATLAB的微分方程的定步长与动步长算法对比解法(附完整代码)一. 内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复