倒立摆：系统分析倒立摆：系统分析

78 阅读 0 评论 52 点赞

我是靠谱客的博主飘逸火，最近开发中收集的这篇文章主要介绍倒立摆：系统分析倒立摆：系统分析，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

倒立摆：系统分析

本教程中使用的主要MATLAB命令为： tf ， ss ， zpkdata ， impulse ， lsim

内容

从主要问题出发，我们衍生了倒立摆系统的开环传递函数。

（1）

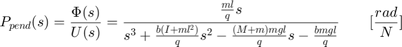
（2）

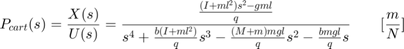
在哪里

（3）

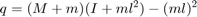
回想一下，上述两个传递函数仅对较高的角度值有效，该角度值

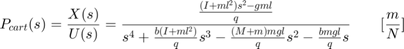是摆锤从垂直向上位置的角度位移。同样，绝对摆角

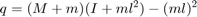等于

。

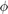有关原始问题的设置以及上述传递函数的派生，请参见“ 倒立摆：系统建模” 页面。

考虑到摆锤对施加于推车上的1-Nsec脉冲的响应，摆锤的设计要求为：

此外，在推车位置，系统对0.2米步距命令的响应要求如下：

开环脉冲响应

创建一个新的 m文件并键入以下命令以创建系统模型（有关获取这些命令的详细信息，请参见主要问题）。

M = 0.5；
m = 0.2；
b = 0.1；
I = 0.006；
g = 9.8；
l = 0.3；
q =（M + m）*（I + m * l ^ 2）-（m * l）^ 2;
s = tf（'s'）;
P_购物车=（（（I + m * l ^ 2）/ q）* s ^ 2-（m * g * l / q））/（s ^ 4 +（b *（I + m * l ^ 2））* s ^ 3 / q-（（M + m）* m * g * l）* s ^ 2 / qb * m * g * l * s / q）；
P_pend =（m * l * s / q）/（s ^ 3 +（b *（I + m * l ^ 2））* s ^ 2 / q-（（M + m）* m * g * l） * s / q-b * m * g * l / q）;
sys_tf = [P_cart; P_pend];
输入= { 'u' };
输出= { 'x' ; 'phi' };
设置（sys_tf，'InputName'，输入）
set（sys_tf，'OutputName'，输出）

现在我们可以检查系统的开环脉冲响应。具体来说，我们将研究系统如何响应使用MATLAB命令 impulse 施加到购物车的脉冲力。将以下命令添加到m文件的末尾，然后在MATLAB命令窗口中运行它，以获取如下所示的关联图。

t = 0：0.01：1;
脉冲（sys_tf，t）;
title（'开环脉冲响应'）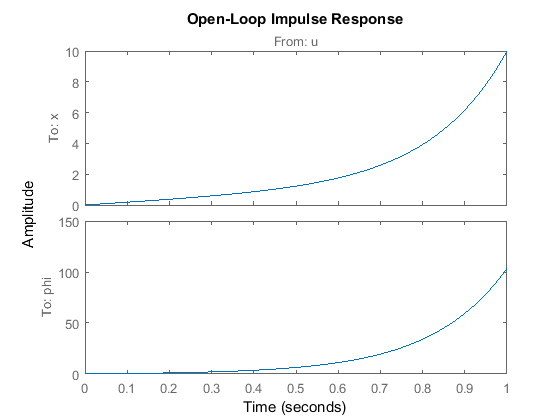

从图中可以看到，系统响应完全不令人满意。实际上，它在开环中不稳定。尽管摆的位置显示增加了超过100弧度（15转），但该模型仅对small有效

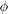。您也可以看到推车的位置无限地向右移动，尽管对推动力输入没有要求。

系统的两极也可以告诉我们有关其时间响应的信息。由于我们的系统具有两个输出和一个输入，因此由两个传递函数来描述。通常，除非存在零极点抵消，否则从多输入多输出（MIMO）系统的每个输入到每个输出的所有传递函数将具有相同的极点（但不同的零点）。我们将使用MATLAB函数 zpkdata 专门检查系统的极点和零点。下面显示的参数 “ v” 将极点和零点作为列向量而不是像元数组返回。

找到摆位置为输出的系统的零点和极点，如下所示：

[零极点] = zpkdata（P_pend，'v'）
零=
0
极数=
5.5651
-5.6041
-0.1428

同样，找到以小车位置作为输出的系统的零点和极点如下：

[零极点] = zpkdata（P_cart，'v'）
零=
4.9497
-4.9497
极数=
0
5.5651
-5.6041
-0.1428

如预测的那样，两个传递函数的极点是相同的。5.5651处的极点指示系统不稳定，因为极点具有正实部。换句话说，极点位于复数s平面的右半部分。这与我们上面观察到的一致。

开环阶跃响应

由于系统的极点具有正的实部，因此其对阶跃输入的响应也将无限制地增长。我们将使用 lsim 命令验证这一点，该命令可用于模拟LTI模型对任意输入的响应。在这种情况下，将使用1-牛顿步进输入。将以下代码添加到您的m文件中，然后在MATLAB命令窗口中运行它，将生成如下图。

t = 0：0.05：10;
u =个（size（t））;
[y，t] = lsim（sys_tf，u，t）;
情节（t，y）
title（'开环阶跃响应'）
轴（[0 3 0 50]）
图例（'x'，'phi'）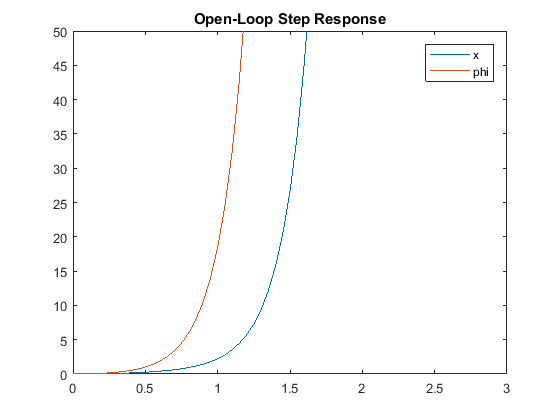

您还可以使用 lsiminfo 命令识别响应的一些重要特征，如下所示。

step_info = lsiminfo（y，t）;
cart_info = step_info（1）
pend_info = step_info（2）
cart_info =
带字段的结构：
稳定时间：9.9959
最小值：0
最小时间：0
最多：8.7918e + 21
上架时间：10
pend_info =
带字段的结构：
稳定时间：9.9959
最小值：0
最小时间：0
最多：1.0520e + 23
上架时间：10

以上结果证实了我们的期望，即系统对阶跃输入的响应是不稳定的。

这些教程包含四个示例控制器：PID，根轨迹，频率响应和状态空间。，以获取更多详细信息。

注意：PID，根轨迹和频率响应示例中的解决方案可能无法产生适用于倒立摆问题的控制器。如前所述，当我们将倒立摆视为单一输入单输出系统时，我们忽略了手推车的位置