一、实验目的
1.掌握利用 Matlab/Simulink仿真平台建立控制系统模型的方法
2.掌握系统的各种模型表述及相互之间的转换关系
3.学习和掌握系统模型连接的等效转换
二、实验原理
1.系统模型的 matlab 综述
系统的模型描述了系统的输入、输出变量以及内部各变量之间的关系,主要有系统传递函数(TF)模型、零极点增益(ZPK)模型和状态空间(ss)模型传 递函数。
(1)传递函数(TF)模型
传递函数是描述线性定常系统输入-输出关系的一种最常用得数学模型,其表达式一般为
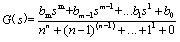
在 matlab 中,直接使用分子分母多项式的行向量表示系统,即
num =[bm, bm-1,… b1, b0]
Den=[an,an-1,…a1,a0]
调用 tf 函数可以建立传递函数 TF 对象模型,调用格式如下:
gtf=tf(num,den)
Tfdata 函数可以从 TF 对象模型中提取分子分母多项式,调用格式如下:
[num,den] = tfdata(Gtf) 返回 cell 类型的分子分母多项式系数
[num,den] = tfdata(Gtf,‘v’) 返回向量形式的分子分母多项式系数
(2)零极点增益(ZPK)模型
传递函数因式分解后可以写成
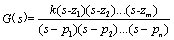
式中,z1,z2,…zm,称为传递函数的零点,p1,p2,…pm称为传递函数的极点,k 为传递系数(系统增益)。
在 matlab 中,直接用[z,p,k]矢量组表示系统,其中 z,p,k 分别表示系统的零 极点及其增益,即:
z=[z1,z2,…zm]
p=[p1,p2,…pm]
k=[k]
调用 zpk 函数可以创建 zpk 对象模型,调用格式如下:
Gzpk = zpk(z,p,k)
同样,MATLAB 提供了 zpkdata 命令用来提取系统的零极点及其增益,调用格式 如下:
[z,p,k] = zpkdata(Gzpk) 返回 cell 类型的零极点及增益
[z,p,k] = zpkdata (Gzpk,’v’) 返回向量形式的零极点及增益
函数 pzmap 可用于求取系统的零极点或绘制系统得零极点图,调用格式如下:
pzmap(G) 在复平面内绘出系统模型的零极点图。
[p,z] = pzmap(G) 返回的系统零极点,不作图。
(3)状态空间(SS)模型
由状态变量描述的系统模型称为状态空间模型,由状态方程和输出方程组成:
x =Ax +Bu
Y= Cx +Du
其中x为n维状态向量,u为r维输入向量,y为m维输出向量,A为n×n方阵, 称为系统矩阵,B为n×r矩阵,称为输入矩阵或控制矩阵,C为m×n矩阵,称为输出矩阵,D为m×r矩阵,称为直接传输矩阵
在matlab中,直接用矩阵组[A,B,C,D]表示系统,调用ss函数可以创建zpk对象模型,调用格式如下:
gss=ss(A,B,C,D)
同样,MATLAB 提供了 ssdata 命令用来提取系统的 A、B、C、D 矩阵,调用格式 如下:
[A,B,C,D] = ssdata (Gss) 返回系统模型的 A、B、C、D 矩阵
(4)三种模型之间的转换
Matlab 实现方法如下:
TF 模型→ZPK 模型:zpk(sys)或 tf2zp(num,den)
TF 模型→SS 模型:ss(sys)或 tf2ss(num,den)
ZPK 模型→TF 模型:tf(sys)或 zp2tf(z,p,k)
ZPK 模型→SS 模型:ss(sys)或 zp2ss(z,p,k)
SS 模型→TF 模型:tf(sys)或 ss2tf(A,B,C,D)
SS 模型→ZPK 模型:zpk(sys)或 ss2zp(A,B,C,D)
2.系统模型的连接
在 MATLAB 中可以直接使用“*”运算符实现串联连接,使用“+”运算符实 现并联连接。反馈系统传递函数求解可以通过命令 feedback 实现,调用格式如 下:
T=feedback(G,H)
T=feedback(G,H,sign)
其中,G 为前向传递函数,H 为反馈传递函数;当 sigh=+1 时,GH 为正反馈系统 传递函数;当 sign=-1 时,GH 为负反馈系统传递函数;默认值是负反馈系统。
串联系统 G(s)=G1(s)G2(s)
并联系统 G(s)=G1(s)+G2(s)
反馈连接 T(s)=G(s)/(1+G(s)H(s))
三、实验内容
1.已知控制系统函数的传递函数如下:
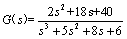
试用 MATLAB 建立系统的传递函数模型、零极点增益模型及系统的状态空间方程模型,并绘制系统零极点图。
2.已知三个系统的传递函数分别为
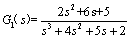
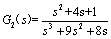
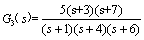
试用 MATLAB 求上述三个系统串联后的总传递函数。
四、实验过程
1.TF/ZPK/SS模型建立
(1)建立传递函数TF模型
(2)定义变量num,den分别表示传递函数分子分母多项式的行向量

(3)调用tf函数建立传递函数TF对象模型

(4)建立零点增益ZPK模型
(5)首先将(1)中的传递函数进行因式分解
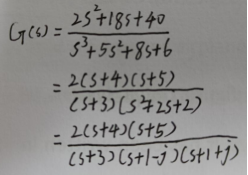
(6)定义变量z,p,k分别为系统的零极点及增益

(7)调用zpk函数建立零点增益模型
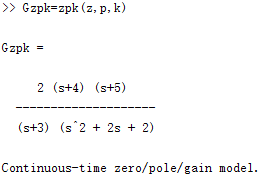
(8)绘制系统零极点图
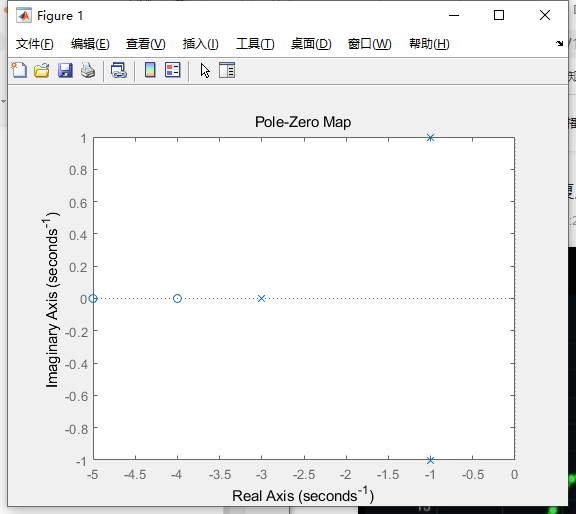
(9)建立系统的状态空间SS模型
(10)由于不知道如何表示状态方程和输出方程,因此系统的状态空间模型不使用正向建立,而使用其他模型转换得到
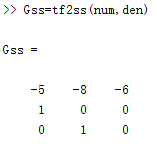
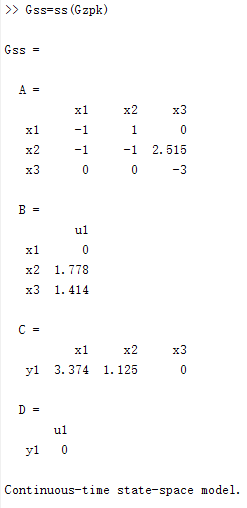
2.传递函数串联实验
(1)分别定义三个传递函数的分子分母多项式行向量

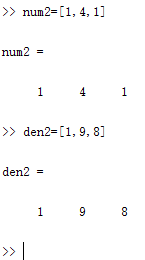

(2)分别调用tf函数构建三个传递函数的TF模型



(3)定义一个新变量G表示总传递函数,并用*表示三个传递函数的串联

最后
以上就是俊秀芒果最近收集整理的关于智能控制基础实验1:控制系统模型一、实验目的二、实验原理三、实验内容四、实验过程的全部内容,更多相关智能控制基础实验1:控制系统模型一、实验目内容请搜索靠谱客的其他文章。






![【[matlab+自控02|自动控制的仿真基础(顺带回顾一点点matlab知识)]】前言一、自控实验常用的两种Matlab程序处理方式二、编写代码文件三、控制系统模型间的相互转换](https://www.shuijiaxian.com/files_image/reation/bcimg9.png)

发表评论 取消回复