无	回到目录	第2章-系统控制原理 -＞ 经典控制理论

第1章 多智能体系统

多智能体系统在自然科学、社会科学等众多领域都有应用，并已成为当前学术界一个重要的研究热点与富有挑战性的研究课题。近年来，针对多智能体系统相关问题的研究得到了快速的发展，并不断涌现了大量的研究成果。移动类智能体，由于其具有自适应性、分散性和自组织性等特点，在实际生产中有着极其重要的应用。因此开展针对移动类多智能体系统的研究，提高其在工程实践中的应用，具有极高的实用价值和工程意义。

本章主要介绍了多智能体系统的基础知识，包括多智能体系统的简介，主要研究内容和相关应用。针对多智能体系统的几种典型控制，详细介绍了一致性控制和编队控制，概述了群集控制、会合控制、同步控制和包容控制。

1.1 多智能体系统简介

1.1.1 研究背景

多智能体系统 (multi-agent system，MAS) 指由许多单个智能体 (agent) 组成，通过智能体之间的相互协调而共同完成一个复杂任务的系统。智能体一般指一个物理的或抽象的实体，具备感知周围环境的能力，并能正确调用自身所具有的知识，对环境做出适当的反应。多智能体协调是一个多学科、多领域融合的新兴工程，其概念最初是受到对自然界中集体行为描述和观察的启发。

在多智能体系统协调控制的应用中，单个智能体设计为具有一定的传感、计算、存储与通信能力的个体，其结构较为简单，所完成的功能比较单一，动态系统的控制输入仅依赖于自身信息和其他有限个智能体的状态信息 [1-3] 。

在现实生活中存在大量多智能体系统的实例，例如鸟群、鱼群和蚁群等，如如图 1.1、图 1.2 和图 1.3 所示，这类系统往往包含数量庞大的个体，但个体本身的智能程度却极为有限。生物界的这些行为在迁徙、躲避捕食者和找寻食物方面具有很大的优势，因此对这些行为的研究吸引了各领域大量研究人员的关注。

1987年，生态学家Reynold [4] 对鸟群、鱼群等群体行为进行仿真，提出了Boid模型。该模型要求智能体满足三个基本规则：1) 避免碰撞：所有个体与邻近个体保持适当间距，以免碰撞；2) 中心汇聚：所有个体试图靠近邻近个体；3) 速度匹配：所有个体试图与邻近个体的速度保持一致。这些规则详尽地描述了系统内每个个体与系统内其他邻近个体交互作用的动态行为 [5] 。此后，Vicsek [6] 在1995年提出了一个简单的模型，以研究在具有生物动机的粒子系统中出现的自我有序运动。后来，在文献 [7-9] 中对集群行为进行了理论的分析。

对于多智能体系统，大量的文献中提出了各种控制体系结构，其中大多数的结构可以被描述为集中式和分布式方案。在集中式系统中，一个连接所有智能体的中央单元拥有全局的团队知识，并通过管理信息以保证任务的完成。因此，先进和昂贵的设备是必要的，以满足所需的技术要求。对于分布式方案，所有的智能体都处于同一级别，拥有相同的设备。每个智能体利用本地传感器获取其邻居 (neighbors) 节点的相对状态信息，然后做出下一步移动和探索环境的决策。每个智能体不需要全局信息，只与相邻的智能体进行通信。

集中式和分布式的方案各有利弊：对于集中式多智能体系统，强大的中央智能体可以极大地提高多智能体系统的整体性能，同时处理器优秀的计算能力和高速通信能力，可以快速有效地将命令发送给所有的智能体。该方案的弊端在于整个系统高度依赖于中心智能体，中央智能体的故障将导致整个任务的失败。集中式方案的鲁棒性不足。此外，对中央智能体的要求较高，导致整个系统的成本较高。而对于分布式系统，使用低成本的传感器和处理器来替代昂贵的核心单元，可以有效地降低系统成本。同时每个智能体的运动只依赖于邻居智能体的局部相对信息，降低了任务的难度。另外，局部智能体的失效不会影响整个系统的性能，因此分散式系统对恶劣环境的容错性更强。该方案的弊端在于分布式控制系统依赖于更复杂的控制策略来协调和优化任务的执行，这在一定程度上限制了系统的性能。并且，通信的带宽和质量限制也会影响系统的整体性能。

多智能体系统分布式协调控制实现了从集中式框架到分布式框架的转变。一般而言，单个智能体动态的崩溃不会影响整个系统的动态演化，也就不会影响整个系统控制目标的实现。这就避免了集中式控制中因中央处理器损坏而导致的整个系统瘫痪，加强了系统的抗干扰性、可扩展性和鲁棒性；同时，通过局部邻居间的信息交互机制，降低了通信成本 [2] 。

综上所述，多智能体系统主要具有以下的特点 [5] ：

(1) 自主性。在多智能体系统中，每个智能体都能管理自身的行为并做到自主的合作或者竞争。

(2) 容错性。智能体可以共同形成合作的系统用以完成独立或者共同的目标，如果某几个智能体出现了故障，其他智能体将自主地适应新的环境并继续工作，不会使整个系统陷入故障状态。

(3) 协作分布性。多智能体系统是分布式系统，智能体之间可以通过合适的策略相互协作完成全局目标。

(4) 可扩展性。多智能体系统本身采用分布式设计，智能体具有高内聚低耦合的特性，使得系统表现出极强的可扩展性。

当今许多机器人控制的想法源自于生物社会。例如，利用各种生物群体特别是鸟类、鱼类、蜜蜂和蚂蚁的简单局部控制规则，在合作机器人系统中采用相似的行为。基于生物行为的启发，文献 [10] 设计了很多代机器鱼用于在3D (3-dimensions) 环境中实施导航。同时，文献 [11] 开发了许多算法，用于跟踪、识别和学习社会动物的行为。这些研究也发现了多智能体系统与单智能体相比的优点。首先，多智能体系统可以降低硬件平台、软件和算法的成本与复杂性，例如一个大型昂贵的机器人可以被几个小型廉价的机器人取代，能够以更低的成本和复杂性来执行任务。其次，多智能体系统可以完成许多单智能体无法有效完成的任务，例如对某一区域的监视任务。此外，具有分布式控制的多智能体系统具有更高的灵活性和鲁棒性，可以通过使用本地邻居智能体之间的通信来减少系统通信和计算的工作量。传感器、通信和控制技术的进步也为多智能体系统的发展提供了良好支持。随着更小、更精确、更可靠的传感器和通信网络的出现，多智能体协同执行任务的策略变得更加有效和智能化。

1.1.2 研究内容

从分层的角度来看，多智能体系统的研究内容主要包含如图 1.4 所示的三部分：单个智能体的动力学模型、智能体之间的通信关系、每个智能体的控制协议。

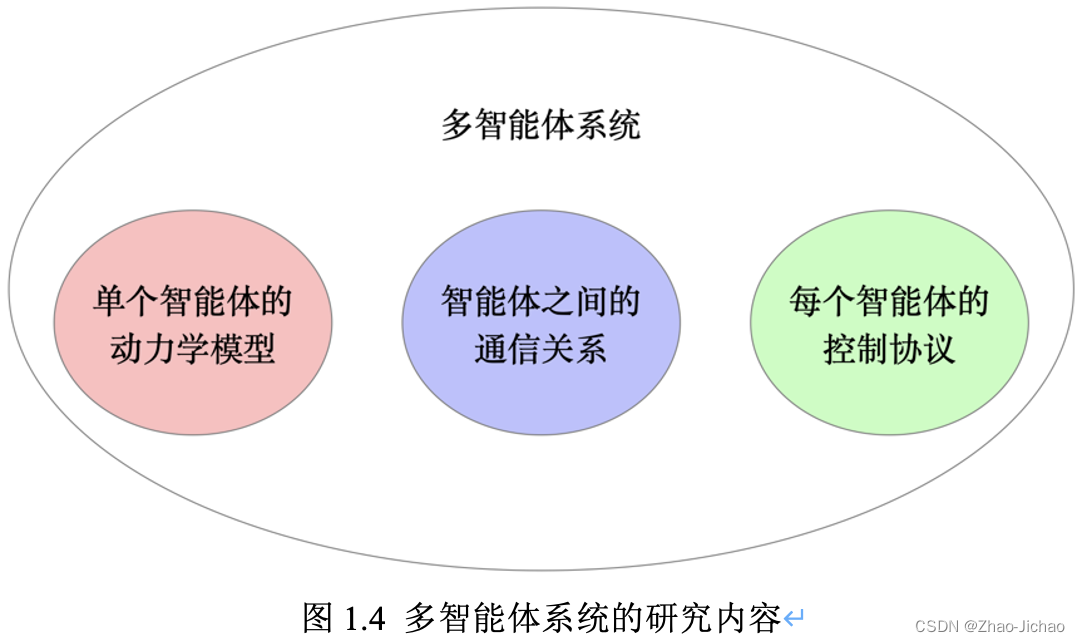
(1) 单个智能体，也被称为单个节点的动力学方程，其反映了单个智能体的内部状态是如何变化的，常用微分方程或差分方程进行表示。根据系统阶次的不同，智能体的动力学模型可以分为一阶 (first-order) 系统、二阶 (second-order) 系统和高阶 (high-order) 系统。根据模型是否是线性的可以分为线性 (linear) 系统和非线性 (non-linear) 系统。根据是否含有时延 (time-delay) 可以分为时延系统或非时延系统。

(2) 智能体之间的通信关系反映了智能体之间的交互关系，即智能体间是相连的可进行信息交互，智能体间不相连而无法进行通信。多智能体之间的通信关系常借助图论 (graph theory) [12] 中的邻接矩阵 (adjacency matrix) 、度矩阵 (degree matrix) 和拉普拉斯矩阵 (Laplacian matrix) 来表示。根据智能体之间通信拓扑是否固定不变，可以将系统分为固定拓扑 (fixed-topology) 和切换拓扑 (switching-topology)。

(3) 每个智能体的控制协议需要根据控制目标来设定。当控制目标确定后，通过控制协议产生各个智能体的控制作用，控制作为输入，输入到系统中的各个智能体中，各个智能体结合控制输入和自身的动力学模型进行自身状态的更新。当所有节点的状态均达到目标状态时，则意味着多智能体系统完成了相应的控制任务。

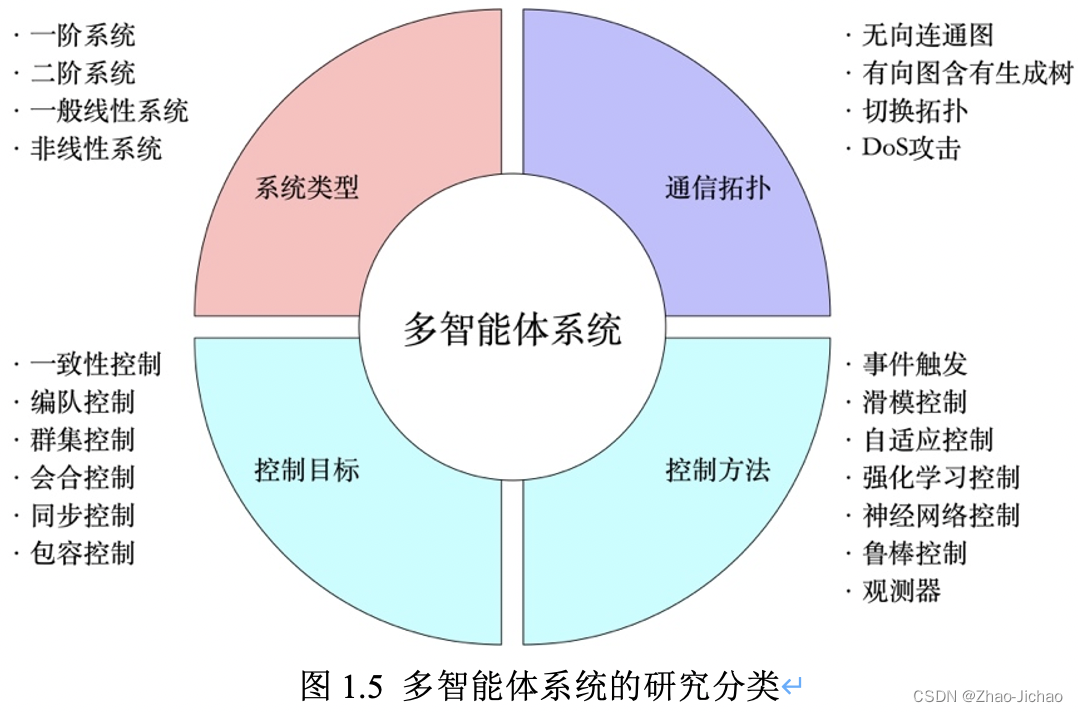
当明确了系统类型和通信拓扑关系后，基本确定了一个多智能体系统。之后就是根据不同的控制目标或控制任务，来设计对应的控制器，使其满足期望的的控制要求。如图 1.5 所示，常见控制目标有一致性控制、编队控制和群集控制等。控制方法包括事件触发控制、滑模控制和自适应控制等。根据不同的控制目标可使用一种或多种控制方法，来设计对应的控制器。

1.1.3 相关应用

近年来，随着控制、通信、计算技术的交叉融合，多体协调控制得到各国学者的广泛关注，并已取得丰硕的研究成果。相对于单体系统，多体系统可以完成更复杂的任务，并具有高效率、高容错性和内在的并行性等优点。现阶段多智能体系统及其相关理论已经被应用在诸多领域。在工程上，多智能体系统中的智能体可以是无人地面车辆 (unmanned ground vehicle，UGV) [13] 、无人驾驶飞行器 (unmanned aerial vehicle，UAV) [14] 、自主水下机器人 (Autonomous Underwater Vehicle，AUV) [15] 、卫星 [16] 和智能电网 [17] 等，它们是具有一定协调能力的控制对象。

图 1.6 为北京理工大学方浩教授团队 [18] 设计的无人车集群平台，还原了牧羊场景。图 1.7 是中国电科电子科学研究院研发的无人机“蜂群”。图 1.8 是中科院自动化所蒲志强教授研发的空地协同系统。图 1.9 是哈佛大学的 Self-Organizing Systems Research Group 团队 [19] 设计的 Kilobit 集群机器人，能够完成集群协同的自组织合作。

在多智能体系统的合作控制中，智能体在本地相互影响，以实现多智能体系统的预期宏观目标。总的来说，多智能体系统的协同控制可以完成多种不同类型的任务。典型的任务包括一致性 [20] 、编队控制 [21-22] 、群集 [23] 、会合 [24-25] 、同步 [26] 和包容 [27-28] 。一致性控制一般被认为是其他控制的基础。此外，多个移动机器人的协同控制可以完成一些专门的任务，如分布式操作 [29] 、未知环境的测绘 [30] 、大型物体的运输 [31] 等。未来，随着无人设备的不断推广及生成过程中自动化水平的不断提高，传统的面向单一对象的控制理论将很难满足实际的控制需求，而多智能体系统因其功能强大、结构灵活、可扩展性强等特点必将得到越来越广泛的应用。

1.2 系统一致性研究

多智能体系统的一致性是研究多智能体系统其他问题的基础。所谓一致性，从控制理论的角度来说，就是指各智能体的状态变量在一定的控制协议和控制器的作用下，最终达到一致 [32] 。一致性的定义为：随着时间的演化，一个多智能体系统中所有智能体的某个或某些状态趋于一致 [33] 。一致性协议是智能体系统中个体之间相互作用的过程，它描述了每个智能体与其相邻的智能体的信息交互过程。其基本思想是每个智能体利用智能体网络传递信息，设计合适的分布式控制算法，最终使智能体动力学与智能体网络拓扑耦合成复杂系统，从而实现状态的一致或者同步。

在智能体的动力学方面，各种系统动力学的一致性问题已被大量研究。系统动力学对多智能体系统的最终一致性状态有很大的影响。例如，具有一阶动力学模型的多智能体系统，其最终的一致状态通常收敛到一个恒定值。然而，二阶动力学模型的系统一致性可能收敛到一个动态最终值，此动态最终值一般是关于时间的函数 [34] 。许多关于一致性问题的早期结果都是基于简单的智能体动力学，如一阶或二阶积分器动力学 [35-37] 。然而，在现实中，大量实际物理系统不能简单地反馈为一阶或二阶动力学模型。例如，对于多无人机系统 [38-39] ，可能需要高阶动力学模型。因此，描述高阶线性多智能体的更复杂动力学模型吸引了大量学者的关注 [40-42] 。之后，将研究结果推广到了非线性多智能体系统 [43-44] 。非线性系统的一致性比线性系统的一致性要复杂得多，困难之处在于非线性使得智能体之间交换信息时增加了一定的限制。二阶 Lipschitz 非线性多智能体系统的一致性控制也得到了一定的研究 [45] 。具有非线性动力学的高阶多智能体系统的一致性问题也得到了研究 [46] 。在之前的研究中，一个常见的假设是，智能体的动力学模型是相同的，并且是精确已知的，这在许多情况下可能是不符合实际情况的。针对动力学模型不同的问题，即异构智能体系统，其一致性控制也得到了大量的关注 [47] 。

智能体之间的通信连接在一致性问题中也起着重要的作用。现有的结果大多都基于固定通信拓扑，即假设拉普拉斯矩阵是一个常数矩阵。当且仅当零是拉普拉斯矩阵的一个简单特征值时，系统是可以达到一致的 [48-49] 。如果零并不是拉普拉斯矩阵的一个简单的特征值，智能体不能达到渐进一致，因为此时至少存在两个单独的子组或组中至少两个智能体不能接收到任何信息。众所周知，当且仅当有向通信拓扑图存在有向生成树或无向通信拓扑图是连通时，零是拉普拉斯矩阵的一个简单特征值 [50-52] 。有向图的结果比无向图的结果复杂得多，主要问题在于与有向图相关的拉普拉斯矩阵通常不是正半定的 [53] 。由于这一不利特性，无向图系统的分解方法不能应用于有向图系统。在实践中，由于传感器的技术限制或链路故障，智能体之间的通信可能无法得到修复。因此，具有切换拓扑的多智能体系统的一致性控制也进行了大量的研究 [54] 。

根据领航者的数量，上述研究也可以大致划分为三组，即无领航者一致性 (consensus without a leader) ，其最终状态值取决于智能体的初始状态；领航-跟随一致性 (leader-follower) ，其中有一个领航者智能体来确定最终一致的状态值；包容控制 (containment control) ，此时智能体网络中有多个领航者。与无领航者一致性相比，领航-跟随一致性和包容控制在提前确定最终一致性状态值方面具有无可比拟的优势。

1.3 系统编队控制研究

除了一致性控制，即将所有智能体都驱动到相同的期望值之外，另一个研究方向是编队控制，即智能体通过局部相互作用形成预先设计好的几何构型。多智能体的编队控制问题是指一组多智能体通过局部的相互作用 (通信、合作、竞争) ，使它们在运动过程中保持预先指定的几何图形，向指定的目标运动，要求每个智能体在运动的过程中，各智能体之间保持一定的距离避免发生碰撞，在运动的道路上能绕过障碍物 [55] 。与一致性控制相比，在编队控制场景下所有智能体的最终状态值更加多样化。例如，在航天器集群中，智能体可以通过一致性控制达到虚拟领航者指定的参考姿态。在达到预期队形的情况下，航天器的位置必须是不同的。

已有许多不同的系统类型用于编队控制，如系统中含有实际领航者 [56] 、虚拟领航者 [57] 、行为领航者 [58] 等。同时，基于一致性的编队控制策略也进行了广泛的研究 [59] 。有学者 [60] 指出，基于一致性的群体控制策略更为普遍，并指出应将许多现有的实际领航者、虚拟领航者和行为领航者的方法作为一致性的特殊情况。早期关于编队控制的研究大多集中在简单的智能体动力学上，如一阶或二阶积分器动力学。然而在现实中，一些实际物理系统不能线性地反馈为一阶或二阶动力学模型。因此关于高阶线性时延多智能体系统的编队控制问题也得到了研究 [59] 。

根据感知变量和被控变量的不同类型，编队控制问题可以分为基于位置 (position) 、位移 (displacement) 和距离 (distance) 的控制 [61] 。当智能体接收到全局坐标系下指定的位置时，它们只感知自己的位置，这称为基于位置的控制。当智能体在全局坐标系中接受方位信息时，它们会感知相邻智能体的相对位置，这种控制称为基于位移的控制。当智能体收到与期望智能体间的距离时，它们会感知邻近的智能体相对于自己的局部坐标系统的相对位置，这称为基于距离的控制。由于为每个智能体指定所需的位置是不现实的，并且为每个智能体提供全局信息会消耗资源，因此采用基于距离的控制算法更为实际。

1.4 系统其他控制研究

1.4.1 群集

群集 (flocking) 。群集是指由大量自主个体组成的集合，在无集中式控制和全局模型的情况下，个体通过局部感知作用和相应的反应行为聚集在一起，使整体呈现出一致行为 [62] 。群集是一种普遍存在的群体行为和自组织现象，通过个体间相对简单的相互作用，它们能够展现出较复杂的集体行为 [63] 。对生物环境的研究后来发展为工程应用中的群集控制问题，它关注的是将多个体的速度协调到一个共同的速度的过程。基 于双积分器模型，即二阶动力学模型，其在平面内 [64] 的群集问题已经得到了研究。同时还包括了具有固定拓扑和切换拓扑结构的系统 [65] ，以及后来增加了避障方案 [66] 。

1.4.2 会合

会合 (rendezvous) 。所谓的会合问题指空间分布的多个个体或者智能体，通过交换邻居局部信息，最终会合于一个期望的区域内，群体中所有个体速度逐渐趋于零，最终静止于某一位置。会合控制的发展源于机器人应用的发展，如一群机器人要合作完成一个任务达到同一个地点，在一片未知区域进行搜索工作，或者一群陆地无人车要达到一个共同的地点等 [62] 。从控制的角度看，会合问题是为每个智能体单独设计局部控制策略，使一个群体中的所有智能体最终在一个未指定的地点会合，而不需要智能体之间进行任何主动通信。有文献 [67] 总结了会合问题的早期表述和算法解决方案，其中智能体具有有限的范围感知能力。

1.4.3 同步

同步 (synchronization) 。并发同步是一种由不同组完全同步的动态系统稳定共存的系统。在科学方法中，耦合非线性振荡器的同步是一个待解决的典型问题。同步化至少涉及两个相互作用的元素，在最近的文献中对一些相互作用的振荡器的行为进行了深入研究。在开创性的工作 [68] 中，观察了两个主从混沌系统的同步现象，并应用于安全通信。参考文献 [69] 通过使用主稳定函数方法解决了振荡器网络的同步稳定性问题。最近，复杂的动力学网络，如小世界和无标度网络的同步性得到了广泛的研究 [70] 。

1.4.4 包容

包容 (containment) 。在领航者-跟随者方案中，跟随者需要作为编队的一部分留在领航者周围，实现这一目标的一个更简单的方法是包容控制。通过将跟随着驱赶到一个由多个领航者包围的凸包中，便不需要关于邻居跟随者的相对速度信息。在避碰场景下，领航者可以通过检测障碍物的位置形成一个 (移动的) 安全区域。然后，在跟随者始终停留在安全区域内的情况下，团队可以安全到达目的地。已有文献研究了单积分器 [71] 、切换拓扑 [72] 、双积分器 [73] 、欧拉-拉格朗日系统 [74] 和一般线性系统 [75] 的包容控制。

1.5 本书结构安排

本书共分为八个章节，内容安排如下。

第 1 章: 多智能体系统。主要介绍了多智能体的基础知识和典型应用。

第 2 章: 系统控制原理。从经典控制理论到线性系统理论，从单输入单输出系统到多输入多输出系统，分别介绍了连续系统和离散系统的模型和求解方法。在线性系统理论中，还介绍了可控性和可观性的概念。针对常用到的李雅普诺夫稳定性分析方法，做了详细的介绍并举例进行了验证。

第 3 章: 数理知识基础。介绍了图的一些基本概念、各种类型图的定义和关于图的矩阵，并根据图的矩阵引出了系统拓扑图的拉普拉斯矩阵。对多智能体系统中可能用到的矩阵进行了分析，介绍了所用矩阵的基础，矩阵的应用和矩阵运算。针对数值微分方程和矩阵微分方程的求解进行了描述。由于运动类智能体需要运行在二维和三维空间中，因此介绍了二维坐标和三维坐标各自的转换矩阵。

第 4 章: 一阶多智能体系统的协同控制以一阶智能体模型为基础，分析了一阶智能体在不同条件下的协同控制问题，具体包括连续时间条件下、离散时间条件下、切换拓扑条件下、含有时延条件下以及系统中存在领航者和跟随者的条件下。

第 5 章: 二阶多智能体系统的协同控制以二阶智能体模型为基础，分析了二阶智能体在不同情况下的协同控制问题，具体包括连续时间情况、离散时间情况、含有时延情况、系统中存在领航者和跟随者的情况和系统的编队控制。

第 6 章: 多无人车系统的协同控制从无人车单个车轮转动开始，系统地介绍了单个无人车的运动原理，建立了单个无人车的动力学模型和运动学模型。无人车的模型被简化成了一阶线性模型，结合线性系统理论，建立了多无人车系统模型，设计了多无人车的一致性控制协议和编队控制协议。对所设计的控制器进行了稳定性分析，通过实验验证了协议的有效性。

第 7 章: 多无人机系统的协同控制从无人机单个螺旋桨旋转开始，系统地介绍了单个无人机的飞行原理，建立了单个无人机的动力学模型和运动学模型。将无人机模型简化成了高阶线性模型，并结合线性系统理论，建立了多无人机系统模型。无人机为高阶系统，存在动态一致性和静态一致性，因此设计了多无人机的动态一致性控制协议、静态一致性控制协议和编队控制协议。对所设计的控制器进行了稳定性分析，通过实验验证了协议的正确性。

第 8 章: 异构系统的协同控制及最优控制基于前文对无人车和无人机的分析，构建了异构系统的合作模型。通过构造转换矩阵解决了无人车和无人机运动空间不匹配的问题。设计了异构系统的动态一致性控制协议、静态一致性控制协议和编队控制协议。结合最优控制理论，分别设计了单个无人车和单个无人机的最优控制律。通过对最优控制律进行分析，给出了异构系统的分布式最优控制协议。

本章涉及的参考文献

[1] 蒲志强, 易建强, 刘振, 等. 知识和数据协同驱动的群体智能决策方法研究综述[J]. 自动化学报, 2022, 48(3): 1-17.

[2] 张志强，王龙. 多智能体系统的事件驱动控制[J]. 控制理论与应用, 2018, 35(08): 1051-1065.

[3] 闵海波，刘源，王仕成，孙富春. 多个体协调控制问题综述[J]. 自动化学报, 2012, 38(10): 1557-1570.

[4] W R C. Flocks, herds and schools: A distributed behavioral model[J]. ACM SIGGRAPH computer graphics, 1987, 21(4): 25-34.

[5] 陈磊，李钟慎. 多智能体系统一致性综述[J]. 自动化博览, 2018, 35(02): 74-78.

[6] VICSEK T, CZIRÓK A, BEN-JACOB E, et al. Novel type of phase transition in a system of self-driven particles[J]. Physical review letters, 1995, 75(6): 1226.

[7] JADBABAIE A, LIN J, MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on automatic control, 2003, 48(6): 988-1001.

[8] OLFATI-SABER R. Flocking for multi-agent dynamic systems: Algorithms and theory[J]. IEEE Transactions on automatic control, 2006, 51(3): 401-420.

[9] SU H, WANG X, LIN Z. Flocking of multi-agents with a virtual leader[J]. IEEE transactions on automatic control, 2009, 54(2): 293-307.

[10] HU H. Biologically inspired design of autonomous robotic fish at Essex[C]//IEEE SMC UK-RI Chapter Conference, on Advances in Cybernetic Systems. [S.l. : s.n.], 2006: 3-8.

[11] BALCH T, DELLAERT F, FELDMAN A, et al. How multirobot systems research will accelerate our understanding of social animal behavior[J]. Proceedings of the IEEE, 2006, 94(7): 1445-1463.

[12] ROSEN K H. 离散数学及其应用[M]. [出版地不详]: 机械工业出版社, 2007.

[13] DONG W, FARRELL J A. Cooperative control of multiple nonholonomic mobile agents[J]. IEEE Transactions on Automatic Control, 2008, 53(6): 1434-1448.

[14] ABDESSAMEUD A, TAYEBI A. Formation control of VTOL unmanned aerial vehicles with communication delays[J]. Automatica, 2011, 47(11): 2383-2394.

[15] BAHR A, LEONARD J J, FALLON M F. Cooperative localization for autonomous underwater vehicles[J]. The International Journal of Robotics Research, 2009, 28(6): 714-728.

[16] REN W, BEARD R W. Decentralized scheme for spacecraft formation flying via the virtual structure approach[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(1): 73-82.

[17] NUNNA H K, DOOLLA S. Multiagent-based distributed-energy-resource management for intelligent microgrids[J]. IEEE Transactions on Industrial Electronics, 2012, 60(4): 1678-1687.

[18] WU C, FANG H, ZENG X, et al. Distributed Continuous-Time Algorithm for Time-Varying Optimization With Affine Formation Constraints[J]. IEEE Transactions on Automatic Control, 2022: 1-8.

[19] RUBENSTEIN M, CORNEJO A, NAGPAL R. Programmable self-assembly in a thousand-robot swarm[J]. Science, 2014, 345(6198): 795-799.

[20] OLFATI-SABER R, MURRAY R. Consensus problems in networks of agents with switching topology and timedelays[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533.

[21] DONG X, YU B, SHI Z, et al. Time-varying formation control for unmanned aerial vehicles: Theories and applications[J]. IEEE Transactions on Control Systems Technology, 2014, 23(1): 340-348.

[22] FAX J, MURRAY R. Information flow and cooperative control of vehicle formations[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1465-1476.

[23] MARTIN S, GIRARD A, FAZELI A, et al. Multiagent flocking under general communication rule[J]. IEEE Transactions on Control of Network Systems, 2014, 1(2): 155-166.

[24] SONG Y, ZHAO W. Multi-agent system rendezvous via refined social system and individual roles[J]. Wseas transactions on systems and control, 2014, 9(1): 526-532.

[25] LIN J, MORSE A S, ANDERSON B D. The multi-agent rendezvous problem[C]//42nd ieee international conference on decision and control (ieee cat. no. 03ch37475): vol. 2. [S.l. : s.n.], 2003: 1508-1513.

[26] SCHENATO L, GAMBA G. A distributed consensus protocol for clock synchronization in wireless sensor network[C]//2007 46th ieee conference on decision and control. [S.l. : s.n.], 2007: 2289-2294.

[27] 王付永. 二阶动态多智能体系统包容控制问题研究[D]. 南开大学, 2019.

[28] JI M, FERRARI-TRECATE G, EGERSTEDT M, et al. Containment control in mobile networks[J]. IEEE Transactions on Automatic Control, 2008, 53(8): 1972-1975.

[29] MARTINOLI A, EASTON K, AGASSOUNON W. Modeling swarm robotic systems: A case study in collaborative distributed manipulation[J]. The International Journal of Robotics Research, 2004, 23(4-5): 415-436.

[30] FOX D, KO J, KONOLIGE K, et al. Distributed multirobot exploration and mapping[J]. Proceedings of the IEEE, 2006, 94(7): 1325-1339.

[31] YANG X, WATANABE* K, IZUMI K, et al. A decentralized control system for cooperative transportation by multiple non-holonomic mobile robots[J]. International Journal of Control, 2004, 77(10): 949-963.

[32] 郭伟强. 基于一致性理论的无人机编队控制器设计[D]. 哈尔滨工业大学, 2013.

[33] 黄家煜. 事件触发控制背景下的二阶多智能体一致性探究[J]. 数学学习与研究, 2019, 3.

[34] CAO Y, YU W, REN W, et al. An Overview of Recent Progress in the Study of Distributed Multi-Agent Coordination[J]. IEEE Transactions on Industrial Informatics, 2013, 9(1): 427-438.

[35] HONG Y, HU J, GAO L. Tracking control for multi-agent consensus with an active leader and variable topology[J]. Automatica, 2006, 42(7): 1177-1182.

[36] REN W, BEARD R W. Consensus algorithms for double-integrator dynamics[J]. Distributed Consensus in Multivehicle Cooperative Control: Theory and Applications, 2008: 77-104.

[37] CAO Y, STUART D, REN W, et al. Distributed containment control for multiple autonomous vehicles with double-integrator dynamics: algorithms and experiments[J]. IEEE Transactions on Control Systems Technology, 2010, 19(4): 929-938.

[38] DING Z. Consensus disturbance rejection with disturbance observers[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5829-5837.

[39] LIU Z, YUAN C, ZHANG Y, et al. A learning-based fault tolerant tracking control of an unmanned quadrotor helicopter[J]. Journal of Intelligent & Robotic Systems, 2016, 84(1): 145-162.

[40] HU Y, LAM J, LIANG J. Consensus of multi-agent systems with Luenberger observers[J]. Journal of the Franklin Institute, 2013, 350(9): 2769-2790.

[41] LI Z, ISHIGURO H. Consensus of linear multi-agent systems based on full-order observer[J]. Journal of the Franklin Institute, 2014, 351(2): 1151-1160.

[42] ZHAO Z, LIN Z. Global leader-following consensus of a group of general linear systems using bounded controls[J]. Automatica, 2016, 68: 294-304.

[43] DING Z. Consensus control of a class of Lipschitz nonlinear systems[J]. International Journal of Control, 2014, 87(11): 2372-2382.

[44] DING Z. Adaptive consensus output regulation of a class of nonlinear systems with unknown high-frequency gain[J]. Automatica, 2015, 51: 348-355.

[45] YU W, CHEN G, CAO M, et al. Second-order consensus for multiagent systems with directed topologies and nonlinear dynamics[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2009, 40(3): 881-891.

[46] YU W, CHEN G, CAO M. Consensus in directed networks of agents with nonlinear dynamics[J]. IEEE Transactions on Automatic Control, 2011, 56(6): 1436-1441.

[47] DING Z. Consensus output regulation of a class of heterogeneous nonlinear systems[J]. IEEE Transactions on Automatic Control, 2013, 58(10): 2648-2653.

[48] LIN Z, FRANCIS B, MAGGIORE M. Necessary and sufficient graphical conditions for formation control of unicycles[J]. IEEE Transactions on automatic control, 2005, 50(1): 121-127.

[49] QU Z. Cooperative control of dynamical systems: applications to autonomous vehicles[M]. [S.l.]: Springer Science & Business Media, 2009.

[50] REN W, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies[J]. IEEE Transactions on automatic control, 2005, 50(5): 655-661.

[51] XI J, CAI N, ZHONG Y. Consensus problems for high-order linear time-invariant swarm systems[J]. Physica A: Statistical Mechanics and its Applications, 2010, 389(24): 5619-5627.

[52] GODSIL C, ROYLE G F. Algebraic graph theory[M]. [S.l.]: Springer Science & Business Media, 2001.

[53] LI Z, DUAN Z. Cooperative control of multi-agent systems: a consensus region approach[M]. [S.l.]: CRC press, 2017.

[54] WEN G, HU G, YU W, et al. Consensus tracking for higher-order multi-agent systems with switching directed topologies and occasionally missing control inputs[J]. Systems & Control Letters, 2013, 62(12): 1151-1158.

[55] 苗国英，马倩. 多智能体系统的协调控制研究综述[J]. 南京信息工程大学学报 (自然科学版), 2013, 5(05): 385-396.

[56] CONSOLINI L, MORBIDI F, PRATTICHIZZO D, et al. Leader-follower formation control of nonholonomic mobile robots with input constraints[J]. Automatica, 2008, 44(5): 1343-1349.

[57] DUAN H, LUO Q, YU Y. Trophallaxis network control approach to formation flight of multiple unmanned aerial vehicles[J]. Science China Technological Sciences, 2013, 56(5): 1066-1074.

[58] BALCH T, ARKIN R C. Behavior-based formation control for multirobot teams[J]. IEEE transactions on robotics and automation, 1998, 14(6): 926-939.

[59] DONG X, XI J, LU G, et al. Formation control for high-order linear time-invariant multiagent systems with time delays[J]. IEEE Transactions on Control of Network Systems, 2014, 1(3): 232-240.

[60] REN W. Consensus strategies for cooperative control of vehicle formations[J]. IET Control Theory & Applications, 2007, 1(2): 505-512.

[61] OH K K, PARK M C, AHN H S. A survey of multi-agent formation control[J]. Automatica, 2015, 53: 424-440.

[62] 王荣浩，邢建春，王平，王春明. 地面无人系统的多智能体协同控制研究综述[J]. 动力学与控制学报, 2016, 14(02): 97-108.

[63] 谢光强，章云. 多智能体系统协调控制一致性问题研究综述[J]. 计算机应用研究, 2011, 28(06): 2035-2039.

[64] TANNER H G, JADBABAIE A, PAPPAS G J. Stable flocking of mobile agents, Part I: Fixed topology[C]//42nd IEEE International Conference on Decision and Control (IEEE Cat. No. 03CH37475): vol. 2. [S.l. : s.n.], 2003: 2010-2015.

[65] TANNER H G, BODDU A. Multiagent navigation functions revisited[J]. IEEE Transactions on Robotics, 2012, 28(6): 1346-1359.

[66] SABER R O, MURRAY R M. Flocking with obstacle avoidance: Cooperation with limited communication in mobile networks[C]//42nd IEEE International Conference on Decision and Control (IEEE Cat. No. 03CH37475): vol. 2. [S.l. : s.n.], 2003: 2022-2028.

[67] ANDO H, OASA Y, SUZUKI I, et al. Distributed memoryless point convergence algorithm for mobile robots with limited visibility[J]. IEEE Transactions on Robotics and Automation, 1999, 15(5): 818-828.

[68] PECORA L M, CARROLL T L. Synchronization in chaotic systems[J]. Physical review letters, 1990, 64(8): 821.

[69] LU W, CHEN T. New approach to synchronization analysis of linearly coupled ordinary differential systems[J]. Physica D: Nonlinear Phenomena, 2006, 213(2): 214-230.

[70] DUAN Z, CHEN G, HUANG L. Disconnected synchronized regions of complex dynamical networks[J]. IEEE Transactions on Automatic Control, 2009, 54(4): 845-849.

[71] FERRARI-TRECATE G, EGERSTEDT M, BUFFA A, et al. Laplacian sheep: A hybrid, stop-go policy for leaderbased containment control[C]//International workshop on hybrid systems: Computation and control. [S.l. : s.n.], 2006: 212-226.

[72] CAO Y, REN W. Containment control with multiple stationary or dynamic leaders under a directed interaction graph[C]//Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference. [S.l. : s.n.], 2009: 3014-3019.

[73] CAO Y, REN W, EGERSTEDT M. Distributed containment control with multiple stationary or dynamic leaders in fixed and switching directed networks[J]. Automatica, 2012, 48(8): 1586-1597.

[74] MEI J, REN W, MA G. Containment control for multiple Euler-Lagrange systems with parametric uncertainties in directed networks[C]//Proceedings of the 2011 American control conference. [S.l. : s.n.], 2011: 2186-2191.

[75] LI Z, REN W, LIU X, et al. Distributed containment control of multi-agent systems with general linear dynamics in the presence of multiple leaders[J]. International Journal of Robust and Nonlinear Control, 2013, 23(5): 534-547.

---

最后

以上就是靓丽手套为你收集整理的第1章-多智能体系统第1章 多智能体系统本章涉及的参考文献的全部内容，希望文章能够帮你解决第1章-多智能体系统第1章 多智能体系统本章涉及的参考文献所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。