UP目录

一、理论基础

二、核心程序

三、测试结果

一、理论基础

        Flocking(有时也称为是warming或herding)，拥有4项简单的规则，把它们组合在一起时，为自治主体群给出一个类似于鸟群、鱼群的群体行为的逼真形式。多智能体集群运动控制技术，是未来大规模无人机集群搜索、大规模自主编队表演技术、超远距无人机集群中继通信等一系列应用场景的技术基石。如何让分布式集群拥有超强避障能力，更是现有研究中的重点。现有的比较成熟的方案是以建模生物体集群运动为核心出发的，通过将障碍物比作虚拟的智能体来实现避障，这种方案又被称为Flocking算法。

       在本方案中，考虑由N个α-智能体组成的智能群体, 其动态方程为:

在Flocking算法中，定向行为规则可以分为分离原则、列队原则、聚合原则、躲避原则
        分离原则：定向时要避免与本地flock同伴拥挤。即定时检测邻近同伴，避免拥挤；
        列队原则：驶向本地flock同伴的平均航向。即检测邻近同伴航向、速度，获取平均值并调整自己；
        聚合原则：定向时朝着本地flock同伴的平均位置移动。即检测邻近同伴，平均位置然后调整其匹配航向；
        躲避原则：使避免撞上局部区域内的障碍或敌人。即“向前看一段距离”，遇到障碍物、敌人调整航向、速度进行躲避。

二、核心程序

....................................................
clear;
close all;
clc;
%% Parameters 初始化参数
num_agents = 100;
t_gap=1;               % 迭代间隔
queue_gap=15;          % 队形间隔
queue_vy=12;
queue_vx=13;
queue_r=40;
r_c=20;                % 交互范围（半径）
k=1.2;                 % 晶格的ratio
d=r_c/k;               % 晶格的scale(表示两两智能体之间的距离（论文中公式5）)
v_0=2;                 % 初始速度
v_limit=0;             % 最大速度
efs = 1;               % sigma-norms parameter 
h=0.4;                 % 设置bump function的分割点（公式10）
d_o = r_c;             
r_c_sigma = sigma_norm(r_c,efs);         % r_c的σ范数
d_sigma = sigma_norm(d,efs);             % d的σ范数
map_width = 400;                         % width of a squre map
map_res = 0.5;                           % width of a grid to play obstacles pixel
c1=0.2;c2=0.5;c3=0.2;c4=0.1;c5=10;c6=0.01;
x = zeros(num_agents,2);                 % current position
x_1 = zeros(num_agents,2);               % previous position
v_1 = zeros(num_agents,2);               % previous velocity
x_r0= zeros(num_agents,2);               % x_r0：用来存储指定的队形信息
v_r_1st_point=300;
path_num = zeros(1000,2,num_agents);
v_r=[1,0];  
%% 生成不同编队队形的智能体坐标

% % 使α-agent群集呈现竖“一”(指定预期坐标)
for a=1:1:num_agents
    b=v_r_1st_point-(a-1)*queue_gap;      
    x_r1(a,2)=b;
end

% % 使α-agent群集呈现V字形
for a=1:1:num_agents
    queue_vy=12;
    b=250-(a-1)*queue_vy;
    x_r2(a,2)=b;
    if a<=num_agents/2
        c=100+queue_vx*(a-1);
        x_r2(a,1)=c;
    else
        c=100+queue_vx*(num_agents-a);
        x_r2(a,1)=c;
    end
end

% % 坐标更新后的竖“一”
for a=1:1:num_agents
    b=v_r_1st_point-(a-1)*queue_gap;
    x_r3(a,2)=b;
    x_r3(a,1)=200+queue_vx*ceil(num_agents/2);
end

% % 使α-agent群集呈现倒V字形
for a=1:1:num_agents
    b=250-(a-1)*queue_vy;
    x_r4(a,2)=b;
    if a<=num_agents/2
        c=340+queue_vx*ceil(num_agents/2)-queue_vx*(a-1);
        x_r4(a,1)=c;
    else
        c=340+queue_vx*ceil(num_agents/2)-queue_vx*(num_agents-a);
        x_r4(a,1)=c;
    end
end

% % 使α-agent群集呈现圆形
for a=1:num_agents
    theta=2*pi/num_agents;
    xo=[450+queue_vx*ceil(num_agents/2),240];
    x_r5(a,1)=xo(1)+queue_r*sin(a*theta);
    x_r5(a,2)=xo(2)-queue_r*cos(a*theta);
end

% % 坐标再次更新后的横“一”
for a=1:1:num_agents
    b=v_r_1st_point-(a-1)*queue_gap;
    x_r6(a,2)=b;
    x_r6(a,1)=580+2*queue_r;
end
%   x_r=[0,150;0,130;0,110]; 
 
% %initializing agents 随机生成坐标
x_1(:,1)=20*rand(num_agents,1);                          % x_1第一列是agent的x初始坐标 
x_1(:,2) = map_width/2*rand(num_agents,1)+map_width/4;   % x_1第二列是agent的y初始坐标
counter = 0;                                             % 用于记录循环次数
%% main loop 主循环
while(true)
    counter=counter+1;
    u_alpha=zeros(num_agents,2);                % alpha-agents correspond to UAVs   初始化alpha agent
    u_gamma=zeros(num_agents,2);                % gamma-objects which model the effect of “collective objective” of a group  初始化gamma agent
    dist_gap = get_gap(x_1);                    % 获取间隔距离
    dist_2 = squd_norm(dist_gap);               % 距离间隔平方和
    dist = sqrt(dist_2);                        % 对距离平方和开方  获得距离
    dist_sigma=sigma_norm(dist_gap,efs);
    adj = bump_func(dist_sigma/r_c_sigma,h);    % 求邻接矩阵
    nbr = zeros(num_agents);                    % 初始化相邻agent矩阵参数
    nbr(dist<=r_c) = 1;                         % 如果两个agent距离小于r_c就算是邻居
    nbr = nbr - diag(diag(nbr));                % set diagonal to 0 取中心元素
    adj = nbr.*adj;                             % 得到邻接矩阵
%% 计算过α-agent的控制输入
% % 这个控制输入主要包括两部分
% % 1.目标对α-agent的吸引力
% % 2.α-agent之间的相互作用力
   
   % % 计算γ-agent对每个α-agent的吸引力
   % u_gamma=-c1*limit(x_1-repmat(x_r,size(u_gamma,1),1),1)-c2*(v_1-repmat(v_r,size(u_gamma,1),1)); 
     u_gamma=-c1*limit(x_1-x_r0,size(u_gamma,1))-c2*(v_1-repmat(v_r,size(u_gamma,1),1)); 
     
   % % 计算α-agent之间的相互作用力
    for a=1:1:num_agents                % 选定一个α-agent
        for b=1:num_agents              % 通过循环的方式依次计算每个α-agent对选定α-agent的作用力的合力
            kk=x_1(b,:)-x_1(a,:);
            u_alpha(a,:)=u_alpha(a,:)+c3*adj(a,b)*phi_func(sigma_norm_2(kk,efs)-d_sigma)*sigma_norm_gradient(kk,efs)+c4*adj(a,b)*(v_1(b,:)-v_1(a,:));   % 将选定α-agent受到的合力一次叠加
%           u_alpha(a,:)=u_alpha(a,:)+c3*nbr(a,b)*action_function( sigma_norm_2(x_1(a,:)-x_1(b,:),efs),r_c_sigma,d_sigma,h )*sigma_norm_gradient(x_1(b,:)-x_1(a,:),efs)+c4*nbr(a,b)*(v_1(b,:)-v_1(a,:));
        end
    end
%% 根据gamma和alpha agent得到v和x（卡尔曼滤波），前提在一个运动周期内速度不变。
    u=u_gamma+u_alpha;                   % 计算控制输入         
    v = v_1 + u*t_gap;                   % 当前时刻的速度估计 = 前一时刻的速度 + 速度增量
    v_1=v;                               % 不考虑噪声，将估计值直接认为当前时刻的真实值
    x(:,1:2) = x_1(:,1:2) + 0.8*v_1*t_gap;   % 根据速度计算当前时刻的位置x，x_1表示前一时刻的位置
    x_1 = x;
    for nn = 1:1:num_agents
       path_num(counter,1,nn) = x(nn,1);
       path_num(counter,2,nn) = x(nn,2);
    end 
%% 队形变换
     if (counter<100)
        x_r1=x_r1+v_r*t_gap;
        x_r0=x_r1;
     elseif (counter<200)
        x_r2=x_r2+v_r*t_gap;
        x_r0=x_r2;
     elseif counter<300
        x_r3=x_r3+v_r*t_gap;
        x_r0=x_r3;
     elseif counter<400
        x_r4=x_r4+v_r*t_gap;
        x_r0=x_r4;
     elseif counter<500
        x_r5=x_r5+v_r*t_gap;
        x_r0=x_r5;
     else
        x_r6=x_r6+v_r*t_gap;
        x_r0=x_r6;
     end

%% plot
    hold off
    plot(x(:,1),x(:,2),'ro');
    hold on
    axis([0 800 0 map_width]);
    plot(x_r0(:,1),x_r0(:,2),'k*');
    if counter>650
         break;
    end
    hold on

%     text(340,150,'★');
    %% 通信agent画线
    for ii=1:1:num_agents
        for jj=1:1:num_agents
            if nbr(ii,jj)>0
                plot([x(ii,1);x(jj,1)],[x(ii,2);x(jj,2)]);
            end
        end
    end
    %% 
    scatter(x(:,1),x(:,2),20,'black')
%      plot(x_r1(:,1),x_r1(:,2),'r*');

    pause(0.1);
  

end
figure(1)
%hold off
for tt = 1:1:num_agents
for t = 1:1:1000
    plot(path_num(t,1,tt),path_num(t,2,tt),'k.','MarkerSize',1);
    hold on;
end
end

......................................

三、测试结果

使用matlab2021a仿真测试结果如下所示：

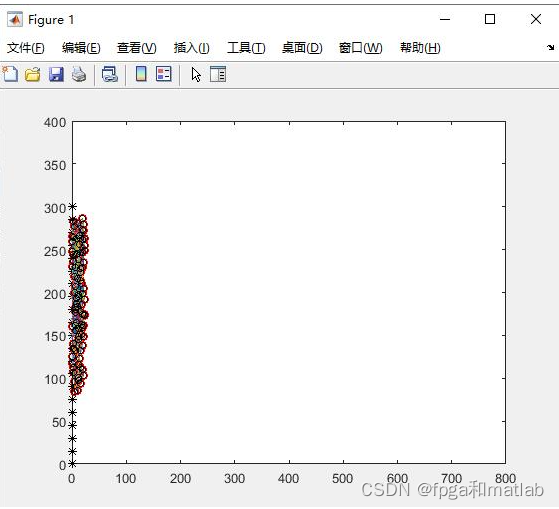
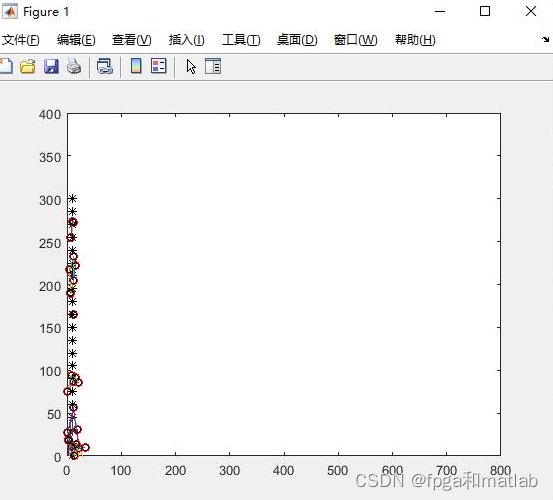
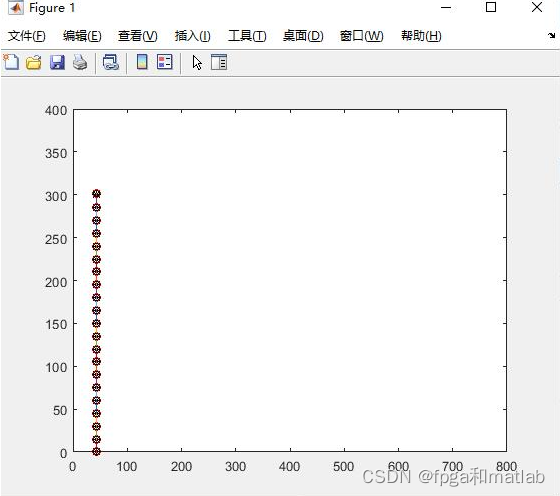
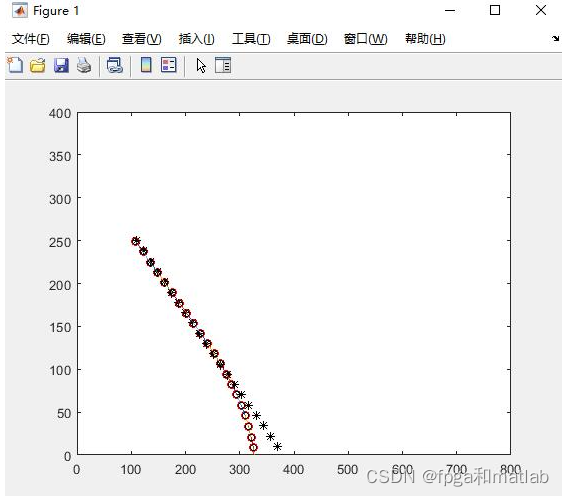
 up0009

最后

以上就是老实小懒虫为你收集整理的基于Flocking算法的多智能体编队matlab仿真一、理论基础二、核心程序三、测试结果的全部内容，希望文章能够帮你解决基于Flocking算法的多智能体编队matlab仿真一、理论基础二、核心程序三、测试结果所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。