【路径规划】基于matlab Dijkstra算法机器人编队路径规划【含Matlab源码 1884期】

⛄一、Dijkstra算法机器人编队路径规划简介

1 传统Dijkstra算法步骤
Dijkstra算法是一种经典的求解最短路径的算法，用于计算一个节点去往其他各个不相关节点的最小移动代价。本思想是把在图中无论如何出现的所有节点分离为2组，第1组包含被准确认定是最短路径的节点，第2组存放待检查的不确定的节点。根据最小移动代价逐渐增大的顺序，逐个将第2组需要检查的节点加入到第1组中，一直到从起始点出发可以到达的所有节点都包含在第1组中。Dijkstra算法运行的主要特征是以机器人抽象的出发点为中心向外层层延伸，直到延伸到整个区域的末端为止。Dijkstra算法一般能够在最终得到最优的路径，但是这个路径偶尔会出现冗余拐点，由于其遍历节点多，所以有时算法的效率不高。Dijkstra算法流程如图2所示。

分别创建2个表，为：START与FINISH。START表中存放环境中已经生成存在但是未经计算的节点，FINISH表中存放所有经过计算考察的节点。

(1）观测寻找在环境路网中离起始源点近而且是没有被计算过的点，把满足调节的点放在START数组中等待检查。

(2）从START表中找出距离起始点最小的点，然后把该点放进FINISH表中。

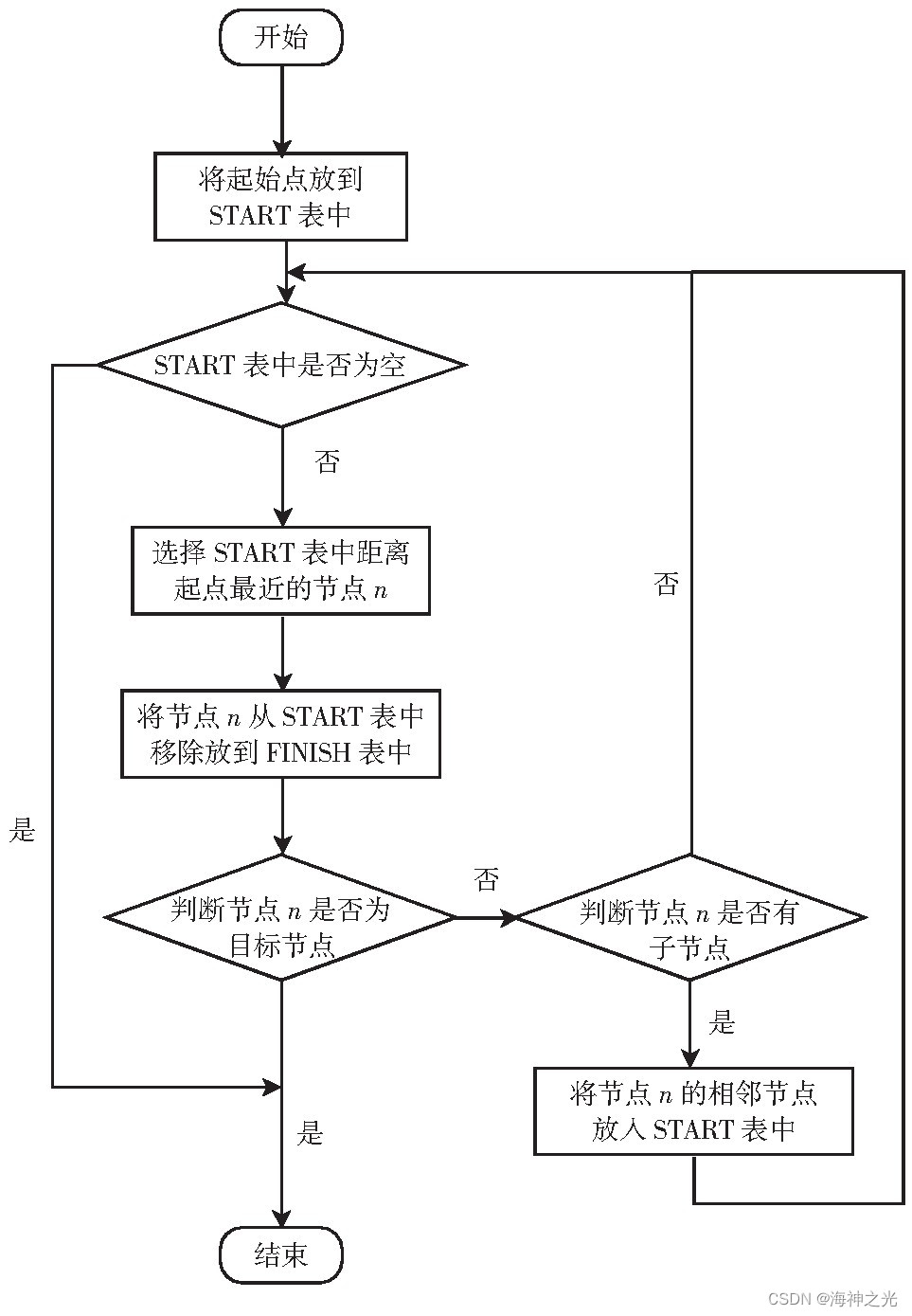
(3）遍历去寻找考察当前此点的子节点，计算出起始源点到这些子节点的距离值，将值存入数组中用来排序，将子节点放在START表中。

(4）重复（2）和（3），直到把START表中的点全部清空，或者找到真正要去的目标点。

2 Dijkstra算法的思想
(1）将环境可视图中出现的节点或是顶点分别加入2个组，其中一组存放经过求解验证为最短路径所经过的顶点，该集合用FINISH表示，刚开始时START表中只有1个起始点，在后面的运算过程中每得到1条最短路径，就把相关节点加入到集合FINISH中。如果全部的顶点都加入到FINISH后，此算法运算完成。另一组存放未经过考察且还未被认定为最短路径的顶点，用START表示。

(2）在将顶点逐渐加入到FINISH表的过程中，在运行算法期间总保持从出发点到FINISH表中各个点的最短路径的长度不超过出发点到START表中任何顶点的最短路径长度。

典型的Dijkstra算法在寻找最优路径的准则上较为单一，以某一个点为中心向外层层扩展就类似于画圆，随着搜索半径的逐渐增大，最后总能找到想要的目标点，但同时最优路径会出现一些无关的冗余点，这样在一定程度上给实际的移动机器人造成寻找路径的困难。如果能够对经典算法的计算准则进行优化，达到减少路径中拐点的目的，就可以减少一大部分机器人寻路所耗费的时间。在大面积环境中使用Dijkstra算法时，由于每次都要从START列表中挑选离原始点最近的点，这样导致规划效率不高，在排序过程消耗很多不必要的工作时间。

⛄二、部分源代码

clc;
clear all;
close all;
cmap = [1 1 1; …
0 0 0; …
1 0 0; …
0 0 1; …
0 1 0; …
1 1 0; …
0.5 0.5 0.5];

colormap(cmap);
%% Define a small map
map_size = 100;
map = false(map_size);
%% Read Picture For Goal Position
picture=imread(‘1.png’); %Read a picture
GoalPosition = ReadPictureForSketch(picture, map_size);
%Problem Defination
nVar = 2; %Number of Variables
VarSize = [1, nVar]; %Matrix Size of Decision Variables
nPop = length(find(GoalPosition==1)); %Population Size(Robot Number)
%Initialization

%The Particle Template
empty_particle.Position = [];
empty_particle.NextPosition = [];
empty_particle.Velocity = [];
empty_particle.Cost = [];
empty_particle.Goal = [];
empty_particle.Best.Position = [];
empty_particle.Best.Cost = [];
empty_particle.Best.Index = [];

%Create Population Array
particle = repmat(empty_particle, nPop, 1);

%Initialize Global Best
GlobalBest.Cost = inf;

%%Initialize Position and Goal
[goal_location_x_array goal_location_y_array] = find(GoalPosition==1);
for i = 1:nPop
[start_x start_y] = ind2sub(size(map), i+0.5*size(map, 1)*size(map, 1));
particle(i).Position = [start_y start_x];
particle(i).Goal = [goal_location_x_array(i) goal_location_y_array(i)];
end

%initial the map to show
map_plot = zeros(map_size);
map_plot(~map) = 1; % Mark free cells
map_plot(map) = 2; % Mark obstacle cells

%%

while(1)
for i = 1:nPop
neighbours = GetSurroundingPositions(particle(i).Position);
MinCost = inf;
particle(i).NextPosition =zeros(VarSize);
%Get the cloest point to goal
for j = 1:size(neighbours, 1)
current_x = neighbours(j, 1);
current_y = neighbours(j, 2);
if (current_x >0 && current_x <= size(map, 1) && current_y >0 && current_y <= size(map, 1)) %the point in the field
if (map_plot(current_x, current_y) ~=2) %the point is not collision
DistanceToGoal = abs(particle(i).Goal(1) - current_x) + abs(particle(i).Goal(2) - current_y);
if(DistanceToGoal < MinCost) %the point is closer than others
particle(i).NextPosition(1) = current_x;
particle(i).NextPosition(2) = current_y;
MinCost = DistanceToGoal;
end
end
end
end
end
GoalExchangeArray = zeros(1, nPop);
for i = 1:nPop
for j = i:nPop
if(GoalExchangeArray(i) || GoalExchangeArray(j))
break
end
GoalExchange = false;
if (isempty(setdiff(particle(i).NextPosition, particle(j).Position)) && isempty(setdiff(particle(j).NextPosition, particle(i).Position)))
GoalExchange = true;
end

% if (isempty(setdiff(particle(i).NextPosition, particle(j).Position)) && isempty(setdiff(particle(j).NextPosition, particle(j).Position)))
% GoalExchange = true;
% end
%
% if (isempty(setdiff(particle(j).NextPosition, particle(i).Position)) && isempty(setdiff(particle(i).NextPosition, particle(i).Position)))
% GoalExchange = true;
% end
if(GoalExchange && (mod(randperm(100,1), 10) > 5))
TempGoal = particle(i).Goal; %exchange the goal
particle(i).Goal = particle(j).Goal;
particle(j).Goal =TempGoal;
particle(i).NextPosition = particle(i).Position; %keep the particel static
particle(j).NextPosition = particle(j).Position;
GoalExchangeArray(i) = 1;
GoalExchangeArray(j) = 1;
end
end
end
%check if the NextPosition will colllision with other particles or not
for i= 1:nPop
if(map_plot(particle(i).NextPosition(1), particle(i).NextPosition(2)) ~=1)
particle(i).NextPosition = particle(i).Position;
end
%Update the map_plot
map_plot(particle(i).Position(1), particle(i).Position(2)) = 1;
particle(i).Position = particle(i).NextPosition;
map_plot(particle(i).Position(1), particle(i).Position(2)) = 4;
end
%change the goal according to the position of the particle randomly
if (mod(randperm(100,1), 11) > 3)
goal_assigned = GoalAssignment(reshape([particle(1:nPop).Position], 2, nPop)‘, reshape([particle(1:nPop).Goal], 2, nPop)’, map_size);
for i=1:nPop
particle(i).Goal(???? = goal_assigned(i, ????;
end
end
%Display
ShowImage(map_plot);
%check the task is finished or not

end

⛄三、运行结果

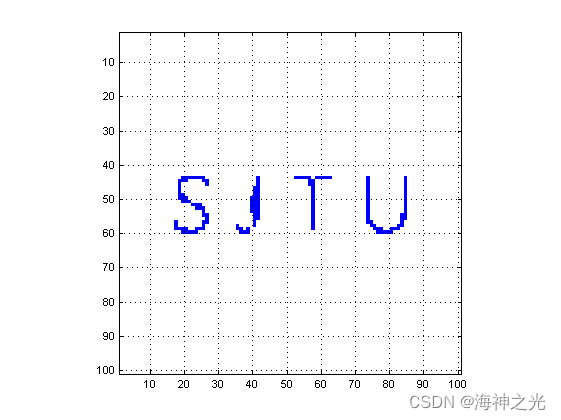
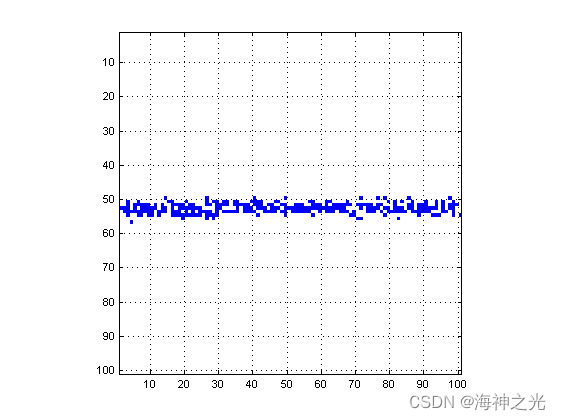
⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]陈智康,刘佳,王丹丹,张运喜.改进Dijkstra机器人路径规划算法研究[J].天津职业技术师范大学学报. 2020,30(03)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

最后

以上就是孝顺画笔为你收集整理的【路径规划】基于matlab Dijkstra算法机器人编队路径规划【含Matlab源码 1884期】的全部内容，希望文章能够帮你解决【路径规划】基于matlab Dijkstra算法机器人编队路径规划【含Matlab源码 1884期】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。