常用的simulink控制工具箱的函数
- 1.构建基本的模型函数
- 1.模型的表示
- (1)传递函数分子/分母多项式模型
- (2)传递函数零极点增益模型
- (3)状态空间模型:
- 2.系统建模
- (1)串联
- (2)并联
- (3)反馈
- 2.时域响应
- 1.脉冲响应:
- 2.阶跃响应:
- 3.一般响应:
- 4.系统的瞬态性能指标
- 3.频率特性的分析
- (1)画 N y q u i s t Nyquist Nyquist图
- (2) B o d e Bode Bode图的绘制
- (3)频率特征量
- 4.系统稳定性分析
- (1)系统特征根
- (2)系统的相对稳定性
- 5.系统校正
- (1)相位超前校正
- (2)相位滞后校正
- (3)相位滞后超前校正
- (4) P I D PID PID校正
- (5) M a t l a b Matlab Matlab代码
- 6.相轨迹图的绘制
- (1)四阶 R u n g e − K u t t a Runge-Kutta Runge−Kutta法
- (2) 相轨迹图的绘制
- 7.线性离散系统
- (1) Z Z Z变换的定义
- (2) Z Z Z变换的性质
- 1.线性性质:
- 2.延迟定理:
- 3.超前定理:
- 4.初值定理:
- 5.终值定理:
- (3) Z Z Z变换表
- (4) M a t l a b Matlab Matlab函数
- (5) M a t l a b Matlab Matlab实现代码
1.构建基本的模型函数
1.模型的表示
模型的表示有3种基本形式:
- 传递函数分子/分母多项式模型
- 传递函数零极点增益模型
- 状态空间模型
(1)传递函数分子/分母多项式模型
G ( s ) = b m s m + b m − 1 s m − 1 + . . . + b 1 s + b 0 a n s n + a n − 1 s n − 1 + . . . a 1 s + a 0 G(s)=frac{b_ms^m+b_{m-1}s^{m-1}+...+b_1s+b_0}{a_ns^n+a_{n-1}s^{n-1}+...a_1s+a_0} G(s)=ansn+an−1sn−1+...a1s+a0bmsm+bm−1sm−1+...+b1s+b0
matlab代码:
n
u
m
=
[
b
m
,
b
m
−
1
,
.
.
.
b
1
,
b
0
]
,
d
e
n
=
[
a
n
,
a
n
−
1
,
.
.
.
a
1
,
a
0
]
G
=
t
f
(
n
u
m
,
d
e
n
)
;
num = [b_m,b_{m-1},...b_1,b_0],den = [a_n,a_{n-1},...a_1,a_0]\ G = tf(num,den);
num=[bm,bm−1,...b1,b0],den=[an,an−1,...a1,a0]G=tf(num,den);
(2)传递函数零极点增益模型
G
(
s
)
=
K
(
s
−
z
0
)
(
s
−
z
1
)
.
.
.
(
s
−
z
m
)
(
s
−
p
0
)
(
s
−
p
1
)
.
.
.
(
s
−
p
n
)
G(s) = Kfrac{(s-z_0)(s-z_1)...(s-z_m)}{(s-p_0)(s-p_1)...(s-p_n)}
G(s)=K(s−p0)(s−p1)...(s−pn)(s−z0)(s−z1)...(s−zm)
matlab代码:
z
=
[
z
0
,
z
1
,
.
.
.
z
m
]
p
=
[
p
0
,
p
1
,
.
.
.
p
n
]
k
=
[
K
]
G
=
z
p
k
(
z
,
p
,
k
)
z = [z_0 ,z_1,...z_m]\ p = [p_0,p_1,...p_n]\ k = [K]\ G = zpk(z,p,k)
z=[z0,z1,...zm]p=[p0,p1,...pn]k=[K]G=zpk(z,p,k)
复杂函数用 c o n v ( x 1 , x 2 ) conv(x1,x2) conv(x1,x2)实现连个向量卷积,用来求多项式乘法。
(3)状态空间模型:
X ˙ = A X + B u Y = C X + D u dot{X}=AX+Bu\ Y=CX+Du X˙=AX+BuY=CX+Du
matlab代码:
s
s
(
A
,
B
,
C
,
D
)
ss(A,B,C,D)
ss(A,B,C,D)
2.系统建模
(1)串联
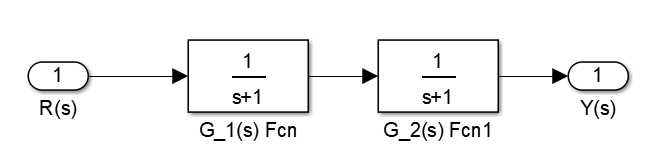 T
(
s
)
=
Y
(
s
)
R
(
s
)
=
n
u
m
d
e
n
=
G
1
(
s
)
G
2
(
s
)
G
1
(
s
)
=
n
u
m
1
d
e
n
1
G
2
(
s
)
=
n
u
m
2
d
e
n
2
[
n
u
m
,
d
e
n
]
=
s
e
r
i
e
s
(
n
u
m
1
,
d
e
n
1
,
n
u
m
2
,
d
e
n
2
)
;
T(s)=frac{Y(s)}{R(s)}=frac{num}{den}=G_1(s)G_2(s)\ G_1(s) = frac{num1}{den1}\ G_2(s) = frac{num2}{den2}\ [num,den] = series(num1,den1,num2,den2);
T(s)=R(s)Y(s)=dennum=G1(s)G2(s)G1(s)=den1num1G2(s)=den2num2[num,den]=series(num1,den1,num2,den2);
T
(
s
)
=
Y
(
s
)
R
(
s
)
=
n
u
m
d
e
n
=
G
1
(
s
)
G
2
(
s
)
G
1
(
s
)
=
n
u
m
1
d
e
n
1
G
2
(
s
)
=
n
u
m
2
d
e
n
2
[
n
u
m
,
d
e
n
]
=
s
e
r
i
e
s
(
n
u
m
1
,
d
e
n
1
,
n
u
m
2
,
d
e
n
2
)
;
T(s)=frac{Y(s)}{R(s)}=frac{num}{den}=G_1(s)G_2(s)\ G_1(s) = frac{num1}{den1}\ G_2(s) = frac{num2}{den2}\ [num,den] = series(num1,den1,num2,den2);
T(s)=R(s)Y(s)=dennum=G1(s)G2(s)G1(s)=den1num1G2(s)=den2num2[num,den]=series(num1,den1,num2,den2);
(2)并联
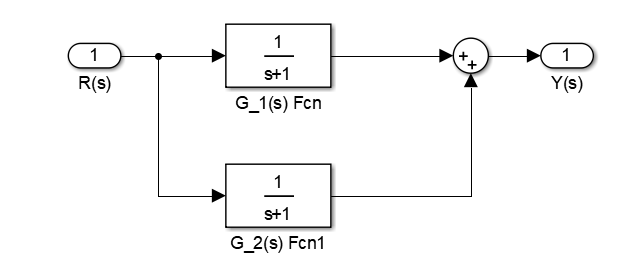
G 1 ( s ) = n u m 1 d e n 1 G 2 ( s ) = n u m 2 d e n 2 T ( s ) = Y ( s ) R ( s ) = n u m d e n [ n u m , d e n ] = p a r a l l e l ( n u m 1 , d e n 1 , n u m 2 , d e n 2 ) G_1(s) = frac{num1}{den1}\ G_2(s) = frac{num2}{den2}\ T(s) = frac{Y(s)}{R(s)} = frac{num}{den}\ [num,den] = parallel(num1,den1,num2,den2) G1(s)=den1num1G2(s)=den2num2T(s)=R(s)Y(s)=dennum[num,den]=parallel(num1,den1,num2,den2)
(3)反馈
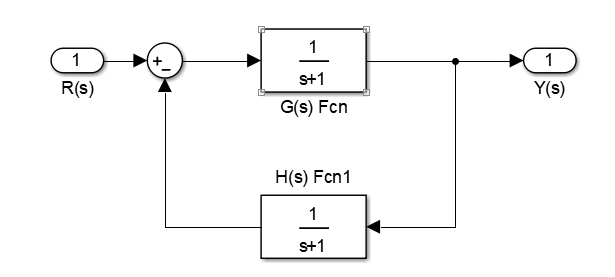
s
i
g
n
:
+
1
:
正
反
馈
,
−
1
:
负
反
馈
G
(
s
)
=
n
u
m
1
d
e
n
1
H
(
s
)
=
n
u
m
2
d
e
n
2
T
(
s
)
=
Y
(
s
)
R
(
s
)
=
n
u
m
d
e
n
[
n
u
m
1
,
d
e
n
1
]
=
f
e
e
d
b
a
c
k
(
n
u
m
1
,
d
e
n
1
,
n
u
m
2
,
d
e
n
2
,
s
i
g
n
)
sign:+1:正反馈,-1:负反馈\ G(s)=frac{num1}{den1}\ H(s) = frac{num2}{den2}\ T(s) = frac{Y(s)}{R(s)} = frac{num}{den}\ [num1,den1] = feedback(num1,den1,num2,den2,sign)\
sign:+1:正反馈,−1:负反馈G(s)=den1num1H(s)=den2num2T(s)=R(s)Y(s)=dennum[num1,den1]=feedback(num1,den1,num2,den2,sign)
状态空间模型与传递函数的转化:
[
d
e
n
,
n
u
m
]
=
s
s
2
t
f
(
F
,
C
,
G
,
D
)
[den,num]=ss2tf(F,C,G,D)
[den,num]=ss2tf(F,C,G,D)。将有理多项式转换成空间状态模型:
[
F
,
C
,
G
,
D
]
=
t
f
2
s
s
(
n
u
m
,
d
e
n
)
;
[F,C,G,D]=tf2ss(num,den);
[F,C,G,D]=tf2ss(num,den);
2.时域响应
1.脉冲响应:
y
y
y:输出响应,
T
T
T:仿真时间,
x
x
x:状态响应(状态空间模型),
s
y
s
sys
sys:模型,
t
t
t:仿真时间
[
y
,
T
,
x
]
=
i
m
p
u
l
s
e
(
s
y
s
,
t
)
;
[y,T,x] = impulse(sys,t);
[y,T,x]=impulse(sys,t);
2.阶跃响应:
y
y
y:输出响应,
T
T
T:仿真时间,
x
x
x:状态响应(状态空间模型),
s
y
s
sys
sys:模型,
t
t
t:仿真时间
[
y
,
T
,
x
]
=
s
t
e
p
(
s
y
s
,
t
)
;
[y,T,x] = step(sys,t);
[y,T,x]=step(sys,t);
3.一般响应:
y
y
y:输出响应,
T
T
T:仿真时间,
x
x
x:状态响应(状态空间模型),
s
y
s
sys
sys:模型,
t
t
t:仿真时间,
u
u
u:输入
[
y
,
T
,
x
]
=
l
s
i
m
(
s
y
s
,
u
,
t
)
;
[y,T,x]= lsim(sys,u,t);
[y,T,x]=lsim(sys,u,t);
4.系统的瞬态性能指标
求 G ( s ) = 50 0.05 s 2 + ( 1 + 50 τ ) s + 50 G(s) = frac{50}{0.05s^2+(1+50tau)s+50} G(s)=0.05s2+(1+50τ)s+5050在不同的 τ tau τ时的单位阶跃响应:
上升时间函数:
function trl = trlf( x,yss,t0 )
%trl 计算上身时间
% 此处显示详细说明
r = 1;
while x(r)<yss
r = r+1;
end
trl = (r-1)*t0;
end
峰值时间函数:
function tpl = tplf( x,t0 )
%tpl 计算峰值时间
% 此处显示详细说明
[ymax,tp] = max(x);
tpl = (tp-1)*t0;
end
最大超调量和调整时间函数:
function [tsl,mpl] = mplf( x,t0,yss ,dlta)
%mplf 计算1001个采样点时的调整时间和最大超调量
% 此处显示详细说明
[ymax,tp] = max(x);
mpl = (ymax-yss)/yss;
s = 1001;
while (x(s)>(1-dlta))&&(x(s)<1+dlta)
s = s-1;
end
tsl = (s-1)*t0;
end
主函数:
t = 0:0.001:1;
yss = 1;
dta = 0.02;
nG = [50,50,50];
tao = [0,0.0125,0.025];
trl = zeros(3,1);%上升时间
tpl = zeros(3,1);%峰值时间
mpl = zeros(3,1);%最大超调量
tsl = zeros(3,1);%调整时间
for i = 1:3
dG(i,:) = [0.05,1+50*tao(i),50];
G(i) = tf(nG(i),dG(i,:));
end
out1 = step(G(1),t);
out2 = step(G(2),t);
out3 = step(G(3),t);
%以下是计算上升时间
trl(1) = trlf( out1,yss,0.001 );
trl(2) = trlf( out2,yss,0.001 );
trl(3) = trlf( out3,yss,0.001 );
%以下是计算峰值时间
tpl(1) = tplf( out1,0.001 );
tpl(2) = tplf( out2,0.001 );
tpl(3) = tplf( out3,0.001 );
%以下是计算最大超调量和调整时间
[tsl(1),mpl(1)] = mplf(out1,0.001,yss,dta);
[tsl(2),mpl(2)] = mplf(out2,0.001,yss,dta);
[tsl(3),mpl(3)] = mplf(out3,0.001,yss,dta);
%输出
disp('tao = 0 时的上身时间 峰值时间 最大超调量 调整时间: ');
disp([trl(1),tpl(1),mpl(1),tsl(1)]);
disp('tao = 0.0125 时的上身时间 峰值时间 最大超调量 调整时间: ');
disp([trl(2),tpl(2),mpl(2),tsl(2)]);
disp('tao = 0.025 时的上身时间 峰值时间 最大超调量 调整时间: ');
disp([trl(3),tpl(3),mpl(3),tsl(3)]);
结果:
>> abc
tao = 0 时的上身时间 峰值时间 最大超调量 调整时间:
0.0640 0.1050 0.3509 0.3530
tao = 0.0125 时的上身时间 峰值时间 最大超调量 调整时间:
0.0780 0.1160 0.1523 0.2500
tao = 0.025 时的上身时间 峰值时间 最大超调量 调整时间:
0.1070 0.1410 0.0415 0.1880
3.频率特性的分析
(1)画 N y q u i s t Nyquist Nyquist图
r
e
:
re:
re:时频特性,
i
m
:
im:
im:虚频特性,
w
:
w:
w:频率范围,
s
y
s
:
sys:
sys:模型,
w
w
w可选频率
[
r
e
,
i
m
,
w
]
=
n
y
q
u
i
s
t
(
s
y
s
,
w
)
;
[re,im,w]=nyquist(sys,w);
[re,im,w]=nyquist(sys,w);
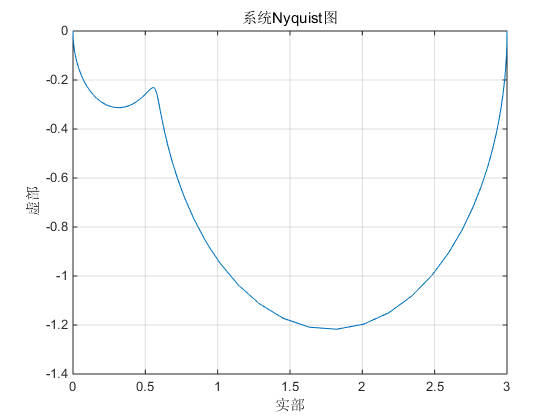
例如:绘制
G
(
s
)
=
24
(
0.25
s
+
0.5
)
(
5
s
+
2
)
(
0.05
s
+
2
)
G(s)=frac{24(0.25s+0.5)}{(5s+2)(0.05s+2)}
G(s)=(5s+2)(0.05s+2)24(0.25s+0.5)的
N
y
q
u
s
i
t
Nyqusit
Nyqusit图:
k = 24;
numG = k*[0.25 0.5];
denG = conv([5,2],[0.05,2]);
sys = tf(numG,denG);
[m,n] = size(re);
[re,im] = nyquist(sys);
for i = 1:n
re1(i) = re(1,1,i);
im1(i) = im(1,1,i);
end
plot(re1,im1);grid on;
xlabel('实部');
ylabel('虚部');
title('系统Nyquist图');
(2) B o d e Bode Bode图的绘制
m
a
g
:
mag:
mag:幅频特性,
p
h
a
s
e
:
phase:
phase:相频特性,
w
:
w:
w:频率范围,
s
y
s
:
sys:
sys:模型
[
m
a
g
,
p
h
a
s
e
,
w
]
=
b
o
d
e
(
s
y
s
,
w
)
;
[mag,phase,w]=bode(sys,w);
[mag,phase,w]=bode(sys,w);
例如:绘制
G
(
s
)
=
24
(
0.25
s
+
0.5
)
(
5
s
+
2
)
(
0.05
s
+
2
)
G(s)=frac{24(0.25s+0.5)}{(5s+2)(0.05s+2)}
G(s)=(5s+2)(0.05s+2)24(0.25s+0.5)的
B
o
d
e
Bode
Bode图:
k = 24;
numG = k*[0.25 0.5];
denG = conv([5,2],[0.05,2]);
sys = tf(numG,denG);
[m,n] = size(re);
w = logspace(-2,3,100);
bode(sys,w);
title('系统Nyquist图');
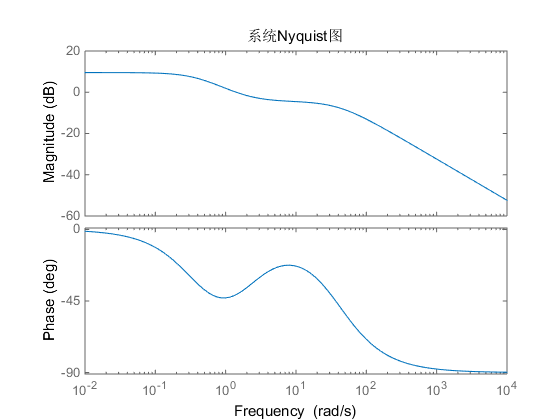
(3)频率特征量
k = 24;
numG = k*[0.25 0.5];
denG = conv([5,2],[0.05,2]);
sys = tf(numG,denG);
w = logspace(-2,4,100);
[Gm,Pm,w]=bode(sys,w);
[m,n] = size(Gm);
for i = 1:n
Gm(i) = Gm(1,1,i);
Pm(i) = Pm(1,1,i);
end
[Mr,k] = max(Gm);
disp('协震峰值是:');
disp(20*log10(Mr));
disp('谐振频率是:');
disp(w(k));
n = 1;
while 20*log10(Gm(n))>=-3
n = n+1;
end
disp('截至频率是:');
disp(w(n));
结果:
协震峰值是:
9.5398
谐振频率是:
0.0100
截至频率是:
3.5112
4.系统稳定性分析
(1)系统特征根
已知特征方程
a
n
s
n
+
a
n
−
1
s
n
−
1
+
.
.
.
+
a
1
s
+
a
0
a_ns^n+a_{n-1}s^{n-1}+...+a_1s+a_0
ansn+an−1sn−1+...+a1s+a0的特征系数是
[
a
n
,
a
n
−
1
,
.
.
.
a
1
,
a
0
]
[a_n,a_{n-1},...a_1,a_0]
[an,an−1,...a1,a0],求根的方法:
r
o
o
t
s
(
[
a
n
,
a
n
−
1
,
.
.
.
a
1
,
a
0
]
)
;
roots([a_n,a_{n-1},...a_1,a_0]);
roots([an,an−1,...a1,a0]);
(2)系统的相对稳定性
s
y
s
:
sys:
sys:系统模型,
G
m
:
Gm:
Gm:幅值裕度,
P
m
:
P_m:
Pm:相位裕度,
W
c
g
:
W_{cg}:
Wcg:相位穿越频率,
W
c
p
:
W_{cp}:
Wcp:幅值穿越频率。
[
G
m
,
P
m
,
W
c
g
,
W
c
p
]
=
m
a
r
g
i
n
(
s
y
s
)
;
[
m
a
g
,
p
h
a
s
e
,
w
]
=
b
o
d
e
(
s
y
s
)
;
→
[
G
m
,
P
m
,
W
c
g
,
W
c
p
]
=
m
a
r
g
i
n
(
m
a
g
,
p
h
a
s
e
,
w
)
[G_m,P_m,W_{cg},W_{cp}]=margin(sys);\ [mag,phase,w]=bode(sys);rightarrow[G_m,P_m,W_{cg},W_{cp}]=margin(mag,phase,w)
[Gm,Pm,Wcg,Wcp]=margin(sys);[mag,phase,w]=bode(sys);→[Gm,Pm,Wcg,Wcp]=margin(mag,phase,w)
5.系统校正
(1)相位超前校正
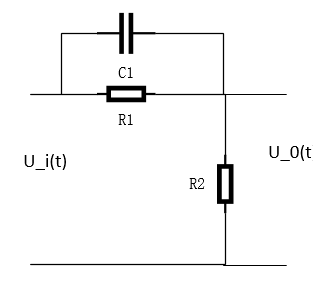
T = R 1 C 1 α = R 1 R 1 + R 2 < 1 G ( s ) = U 0 ( s ) U i ( s ) = 1 + T s 1 + α T s T=R_1C_1\alpha = frac{R_1}{R_1+R_2}<1\ G(s) = frac{U_0(s)}{U_i(s)}=frac{1+Ts}{1+alpha Ts}\ T=R1C1α=R1+R2R1<1G(s)=Ui(s)U0(s)=1+αTs1+Ts
(2)相位滞后校正
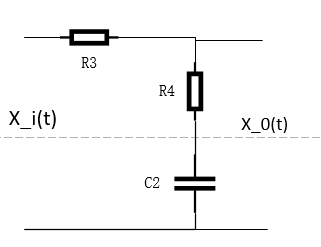
β = R 3 + R 4 R 4 > 1 T = R 4 C 2 G ( s ) = 1 + T s 1 + β T s beta=frac{R_3+R_4}{R_4}>1\ T = R_4C_2\ G(s) = frac{1+Ts}{1+beta Ts} β=R4R3+R4>1T=R4C2G(s)=1+βTs1+Ts
(3)相位滞后超前校正
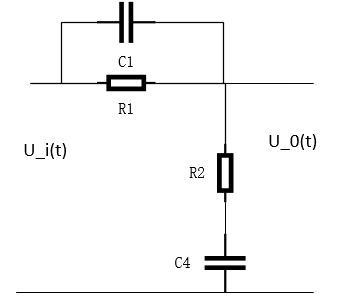
T 1 = R 1 C 1 , T 2 = R 2 C 4 β = R 1 + R 2 R 2 > 1 G ( s ) = ( T 1 s + 1 ) ( T 2 s + 1 ) ( T 1 β s + 1 ) ( β T 2 s + 1 ) T_1 = R_1C_1,T_2 = R_2C_4\ beta=frac{R_1+R_2}{R_2}>1\ G(s) = frac{(T_1s+1)(T_2s+1)}{(frac{T_1}{beta}s+1)(beta T_2s+1)} T1=R1C1,T2=R2C4β=R2R1+R2>1G(s)=(βT1s+1)(βT2s+1)(T1s+1)(T2s+1)
(4) P I D PID PID校正
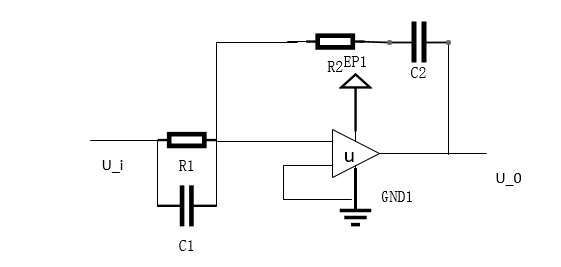
T i = R 1 C 1 + R 2 C 2 T d = R 1 C 1 R 2 C 2 R 1 C 1 + R 2 C 2 K p = R 1 C 1 + R 2 C 2 R 1 C 2 G ( s ) = K p ( 1 + 1 T i s + T d s ) T_i=R_1C_1+R_2C_2\ T_d = frac{R_1C_1R_2C_2}{R_1C_1+R_2C_2}\ K_p=frac{R_1C_1+R_2C_2}{R_1C_2}\ G(s)=K_p(1+frac{1}{T_is}+T_ds) Ti=R1C1+R2C2Td=R1C1+R2C2R1C1R2C2Kp=R1C2R1C1+R2C2G(s)=Kp(1+Tis1+Tds)
(5) M a t l a b Matlab Matlab代码
function y = PID_fun(num,den,kp,ki,kd,ts,numbers,yd,M)
%PID_fun 阶跃信号
% num:连续函数分子
% den:连续函数分母
% k_p,k_i,k_d:PID参数
% ts:采样时间
% numbers:采样点数目
% yd:输入信号
% M:阈值
% clc;
% clear;
sys = tf(num,den);
dsys = c2d(sys,ts,'z');
[numz,denz] = tfdata(dsys,'v');
u_1 = 0;u_2 = 0;u_3 = 0;
y_1 = 0; y_2 = 0; y_3 = 0;
x = [0 0 0]';
error_1 = 0;
error_2 = 0;
for k = 1:1:numbers
time(k) = k*ts;
du(k) = kp*x(1)+kd*x(2)+ki*x(3);
u(k) = u_1 + du(k);
if u(k)>=M
u(k) = M;
end
if u(k)<=-M
u(k) = -M;
end
y(k) = (-denz(2)*y_1 - denz(3)*y_2+numz(2)*u_1+numz(3)*u_2)/denz(1);%z变换延迟定理
error = yd(k) - y(k);
u_3 = u_2;u_2 = u_1;u_1 = u(k);
y_3 = y_2;y_2 = y_1;y_1 = y(k);
x(1) = error - error_1;
x(2) = error - 2*error_1+error_2;
x(3) = error;
error_2 = error_1;
error_1 = error;
end
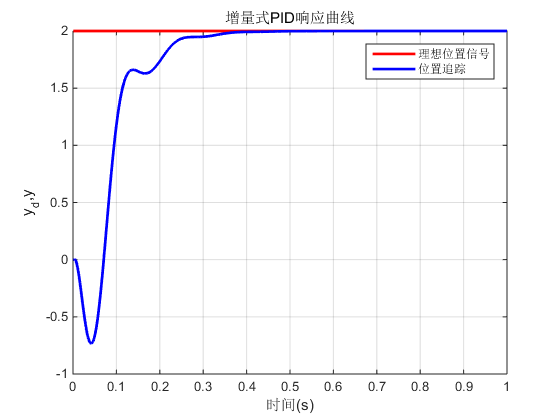
figure;
plot(time,yd,'r',time,y,'b','linewidth',2);
xlabel('时间(s)');ylabel('y_d,y');
grid on
title('增量式PID响应曲线');
legend('理想位置信号','位置追踪');
end
调用
>> y = PID_fun([40 10],[1 50 0],8,0.1,10,0.001,1000,2*ones(1000,1),10);
反馈校正和顺馈校正此处就不再赘述了。
6.相轨迹图的绘制
(1)四阶 R u n g e − K u t t a Runge-Kutta Runge−Kutta法
设
t
t
t为自变量时间,
y
y
y为因变量,微分方程的形式
y
˙
=
f
(
t
,
y
)
dot{y}=f(t,y)
y˙=f(t,y)。
′
o
d
e
f
u
n
′
'odefun'
′odefun′:包含微分方程(组)的
M
M
M文件,
t
s
:
ts:
ts:自变量取值,
y
0
:
y_0:
y0:变量
y
y
y的初值,
p
i
:
p_{i}:
pi:文件内的附加参数。
[
t
,
y
]
=
o
d
e
45
(
′
o
d
e
f
u
n
′
,
t
s
,
y
0
,
[
]
,
p
1
,
p
2
,
.
.
.
)
;
[t,y] = ode45('odefun',t_s,y_0,[],p_1,p_2,...);
[t,y]=ode45(′odefun′,ts,y0,[],p1,p2,...);
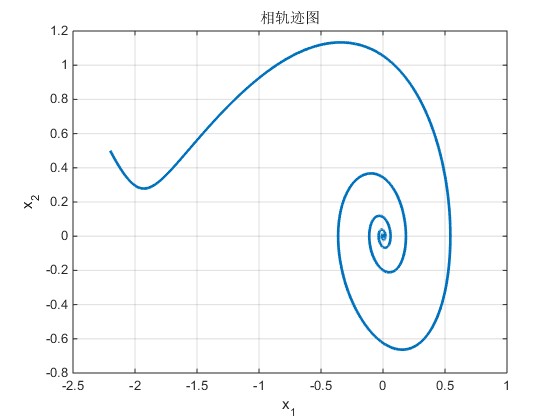
(2) 相轨迹图的绘制
做出
x
¨
+
0.5
x
˙
+
2
x
+
x
2
=
0
ddot{x}+0.5dot{x}+2x+x^2=0
x¨+0.5x˙+2x+x2=0在初值为
(
−
2.2
,
0.5
)
T
(-2.2,0.5)^T
(−2.2,0.5)T时的相轨迹图:
令
x
1
=
x
,
x
2
=
x
1
˙
x_1 = x,x_2=dot{x_1}
x1=x,x2=x1˙:
x
1
˙
=
x
2
x
2
˙
=
−
0.5
x
2
−
2
x
1
−
x
1
2
dot{x_1} =x_2\ dot{x_2} = -0.5x_2-2x_1-x_1^2
x1˙=x2x2˙=−0.5x2−2x1−x12
函数:
function y = odefun1( t,x,p1 )
%UNTITLED 此处显示有关此函数的摘要
% 此处显示详细说明
y = [x(2);-p1*x(2)-2*x(1)-x(1)^2];
end
主函数:
t = 0:0.01:100;
x0 = [-2.2;0.5];
p1 = 0.5;
[t,y] = ode45(@odefun1,t,x0,[],p1);
plot(y(:,1),y(:,2),'linewidth',2);
grid on;xlabel('x_1');ylabel('x_2');
title('相轨迹图');
7.线性离散系统
(1) Z Z Z变换的定义
连续信号
x
(
t
)
x(t)
x(t),采样输出信号
x
∗
(
t
)
x^*(t)
x∗(t),单位脉冲序列
δ
s
(
t
)
delta_s(t)
δs(t),采样周期
T
T
T
x
∗
(
t
)
=
∑
n
=
0
∞
x
(
n
T
)
δ
(
t
−
n
T
)
当
n
≥
0
时
,
对
上
面
进
行
L
a
p
l
a
c
e
变
换
:
L
[
x
∗
(
t
)
]
=
∑
n
=
0
∞
x
(
n
T
)
∫
0
∞
δ
(
t
−
n
T
)
e
−
s
t
d
t
=
∑
n
=
0
∞
x
(
n
T
)
e
−
s
n
T
x^*(t)=sum_{n=0}^{infty}x(nT)delta(t-nT)\ 当n geq 0时,对上面进行Laplace变换:\ L[x^*(t)]=sum_{n=0}^{infty}x(nT)int_0^{infty}delta(t-nT)e^{-st}dt=sum_{n=0}^{infty}x(nT)e^{-snT}
x∗(t)=n=0∑∞x(nT)δ(t−nT)当n≥0时,对上面进行Laplace变换:L[x∗(t)]=n=0∑∞x(nT)∫0∞δ(t−nT)e−stdt=n=0∑∞x(nT)e−snT
如果我们让
z
=
e
s
T
z=e^{sT}
z=esT得到
Z
Z
Z变换的变换式:
Z
[
x
(
t
)
]
=
X
(
z
)
=
∑
n
=
0
∞
x
(
n
T
)
z
−
n
Z[x(t)]=X(z)=sum_{n=0}^{infty}x(nT)z^{-n}
Z[x(t)]=X(z)=n=0∑∞x(nT)z−n
(2) Z Z Z变换的性质
1.线性性质:
Z [ a x 1 ( t ) + b x 2 ( t ) ] = a X 1 ( z ) + b X 2 ( z ) Z[ax_1(t)+bx_2(t)]=aX_1(z)+bX_2(z) Z[ax1(t)+bx2(t)]=aX1(z)+bX2(z)
2.延迟定理:
设 Z [ x ( t ) ] = X ( z ) , 且 t < 0 时 , x ( t ) = 0 , 则 : Z [ x ( t − m T ) ] = z − m X ( z ) 设Z[x(t)] = X(z),且t<0时,x(t)=0,则: Z[x(t-mT)]=z^{-m}X(z) 设Z[x(t)]=X(z),且t<0时,x(t)=0,则:Z[x(t−mT)]=z−mX(z)
3.超前定理:
设 Z [ x ( t ) ] = X ( z ) , 则 : Z [ x ( t + m T ) ] = z m [ X ( z ) − ∑ k = 0 m − 1 x ( k T ) z − k ] 设Z[x(t)] = X(z),则: Z[x(t+mT)]=z^m[X(z)-sum_{k=0}^{m-1}x(kT)z^{-k}] 设Z[x(t)]=X(z),则:Z[x(t+mT)]=zm[X(z)−k=0∑m−1x(kT)z−k]
4.初值定理:
设 Z [ x ( t ) ] = X ( z ) , 则 : x ( 0 ) = l i m z → ∞ X ( z ) 设Z[x(t)]=X(z),则: x(0)=lim_{z rightarrow infty}X(z) 设Z[x(t)]=X(z),则:x(0)=limz→∞X(z)
5.终值定理:
设 Z [ x ( t ) ] = X ( z ) , 且 ( z − 1 ) X ( z ) 的 全 部 极 点 位 于 单 位 圆 内 , 则 : x ( ∞ ) = l i m z → 1 [ X ( z ) ( z − 1 ) ] 设Z[x(t)]=X(z),且(z-1)X(z)的全部极点位于单位圆内,则:x(infty)=lim_{z rightarrow 1}[X(z)(z-1)] 设Z[x(t)]=X(z),且(z−1)X(z)的全部极点位于单位圆内,则:x(∞)=limz→1[X(z)(z−1)]
(3) Z Z Z变换表
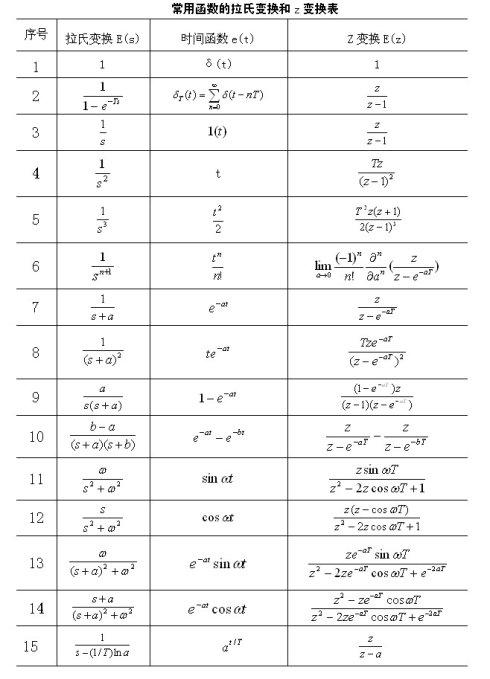
Z [ a k ] = z z − a Z [ a k c o s k π ] = z z + a Z[a^{k}]=frac{z}{z-a}\ Z[a^kcoskpi]=frac{z}{z+a} Z[ak]=z−azZ[akcoskπ]=z+az
稳定性分析和校正设计就不描述了。
(4) M a t l a b Matlab Matlab函数
若
G
(
z
)
=
n
u
m
d
(
z
)
d
e
n
d
(
z
)
G(z) = frac{numd(z)}{dend(z)}
G(z)=dend(z)numd(z),
T
T
T为采样时间,
′
z
o
h
′
'zoh'
′zoh′为零阶保持,传递函数
G
p
(
s
)
=
n
u
m
(
s
)
d
e
n
(
s
)
G_p(s)=frac{num(s)}{den(s)}
Gp(s)=den(s)num(s),且
G
(
z
)
G(z)
G(z)对应着传递函数
G
p
(
s
)
G_p(s)
Gp(s),则:
[
n
u
m
d
,
d
e
n
d
]
=
c
2
d
m
(
n
u
m
,
d
e
n
,
T
,
′
z
o
h
′
)
;
[numd,dend] = c2dm(num,den,T,'zoh');
[numd,dend]=c2dm(num,den,T,′zoh′);
而如果求得逆的话:
[
n
u
m
,
d
e
n
]
=
d
2
c
m
(
n
u
m
d
,
d
e
n
d
,
T
,
′
z
o
h
′
)
;
[num,den] = d2cm(numd,dend,T,'zoh');
[num,den]=d2cm(numd,dend,T,′zoh′);
如果要求任意输入响应,
y
y
y:输出响应,
x
:
x:
x:状态响应,
u
:
u:
u:输入,
G
(
s
)
=
n
u
m
d
e
n
G(s)=frac{num}{den}
G(s)=dennum,
k
:
k:
k:指定的采样数。
[
y
,
x
]
=
d
l
s
i
m
(
n
u
m
,
d
e
n
,
u
,
k
)
;
[y,x]=dlsim(num,den,u,k);
[y,x]=dlsim(num,den,u,k);
(5) M a t l a b Matlab Matlab实现代码
num = 1;den = [1,1,0];
T = 1;
[nz,dz] = c2dm(num,den,T,'zoh');
printsys(nz,dz,'z');
输出:
num/den =
0.36788 z + 0.26424
------------------------
z^2 - 1.3679 z + 0.36788
最后
以上就是朴素狗最近收集整理的关于常用的simulink控制工具箱的函数的全部内容,更多相关常用内容请搜索靠谱客的其他文章。








发表评论 取消回复