汽车坐标系与全局坐标系的变换_坐标变换

总述

文章的题目是“坐标变换”，但事实上，下面我们将讨论两部分的内容：坐标系变换和图形变换。而二者均与“坐标”有关，因此将题目取为“坐标变换”。

坐标系变换，指的是通过变换的思想，建立起不同种类坐标系之间的联系。这一部分的讨论以笛卡尔坐标系（平面直角坐标系）为基础，讨论斜坐标系、极坐标系、空间直角坐标系、柱坐标系、球面坐标系等与之的联系。

图形变换，指通过改变图形方程中的某些参数，或通过坐标轴的变换，引起图形形状的变化。

坐标系变换

1. 笛卡尔坐标系（平面直角坐标系）

下面是我们常见的笛卡尔坐标系，又称为平面直角坐标系。

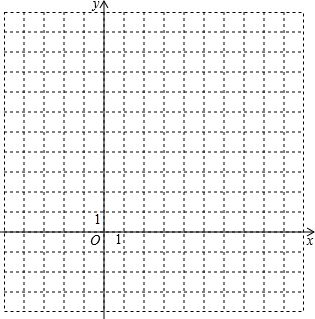
其本质是两个分别沿x轴、y轴正方向的单位向量。对于平面上的任意一点

，存在唯一的向量

与之对应，向量

，

。如果我们取

，

，那么我们可以将点A对应的向量

因此从本质上讲，构成平面直角坐标系的基本元素是：原点、i

、

。

2. 斜坐标系

既然我们说，平面直角坐标系是由两个相互垂直的向量构成，那么如果我们让这两个向量不垂直呢？这样我们就得到了斜坐标系，如下图。

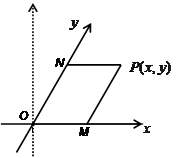
而对于向量来说，垂直与不垂直，其都满足向量加减的线性运算法则，这一点斜坐标系于平面直角坐标系并无区别；但是二者的不同点在于，直角坐标系的两个单位向量的内积为0，而斜坐标系两个单位向量的内积不为0。

具体斜坐标系下的点的坐标以及曲线方程与在直角坐标下的异同，留给读者思考，在这里不再赘述。

3. 极坐标系

下面是我们常见到的极坐标系。

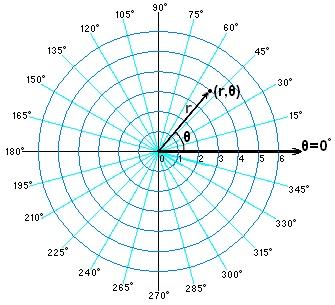
既然我们要说各种坐标系之间的联系，那么认真的朋友们可能会心生疑问，如果说笛卡尔坐标系由两个垂直的向量构成，那么极坐标系呢？我们知道极坐标系有一个极轴，如果把极轴作为一个“向量”，那么另一个向量在哪里呢？

我们先抛开这些不谈，先从变换的角度去想这件事。既然是“变”，那就存在一个“动态”的过程，通过什么样的过程可以将直角坐标系变为极坐标系呢？

细心的朋友可能会发现，极坐标系与平面直角坐标系中有一个共同的东西（至少两幅图中都有）——网格。不同的是，直角坐标系的网格是方形的，而极坐标系中是圆形网格。再来想一想我们刚刚说过的斜坐标系，它的网格应该是什么样子的呢？——是平行四边形的。

网格中的一条线，由某一个坐标相同的无数个点构成。斜坐标系中将y轴变动，网格也随之变动，那么极坐标系呢？是不是也是y轴发生了某种变动呢？

我们来考虑下面这个特殊的“坐标系”。

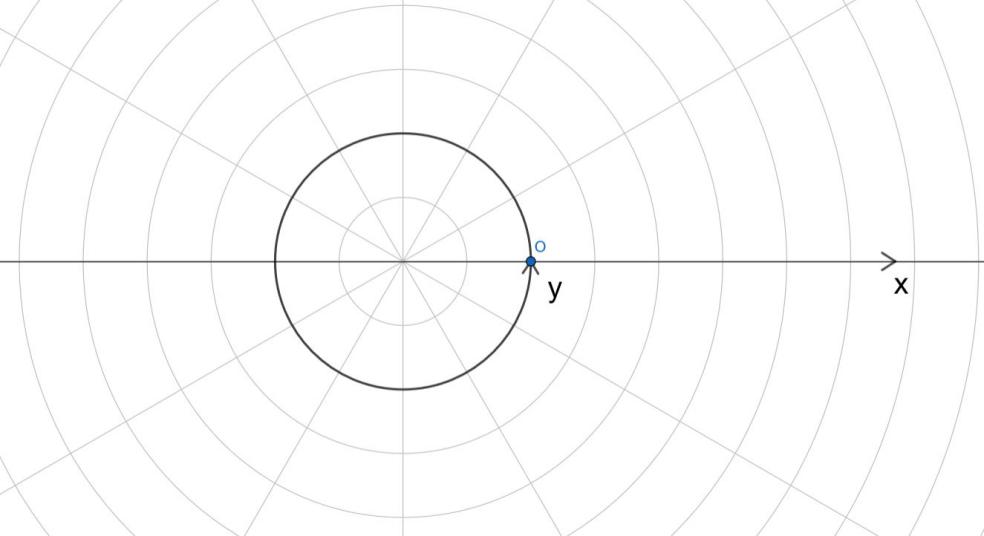
我们画了一个圆形的“y轴”。由x坐标相同的无数个点，我们画出了一个个同心圆，由y坐标相同的无数个点，我们画出来了一条条射线，从而组成了我们熟悉的圆形网格。

但是这个坐标系和极坐标系还有一点不同，就是原点的位置。上述坐标系的原点并不是圆形网格的中心，而极坐标系中的原点（极点）就是圆形网格的中心。如何解决这个问题呢？

其实很简单。我们设圆形y轴的半径为

（

），那么上述坐标系的原点与圆形网格中心的距离就是

，这时我们只需取

趋近于0即可。

也就是说，我们认为在极坐标系的极点处，有一个有向（逆时针）点圆（半径为0的圆），这个有向点圆就是我们苦苦寻找的y轴。

因此如果我们说平面直角坐标系是“线性”的，那么极坐标系就是某冲程度上的“扭曲”，将原本是一条直线的y轴“扭曲”成为一个圆，从而形成了极坐标系。

举一个例子，y=x是我们非常熟悉的一条平面直角坐标系中的直线，对应到极坐标系中，便成了

，下面我把它们画在一起。

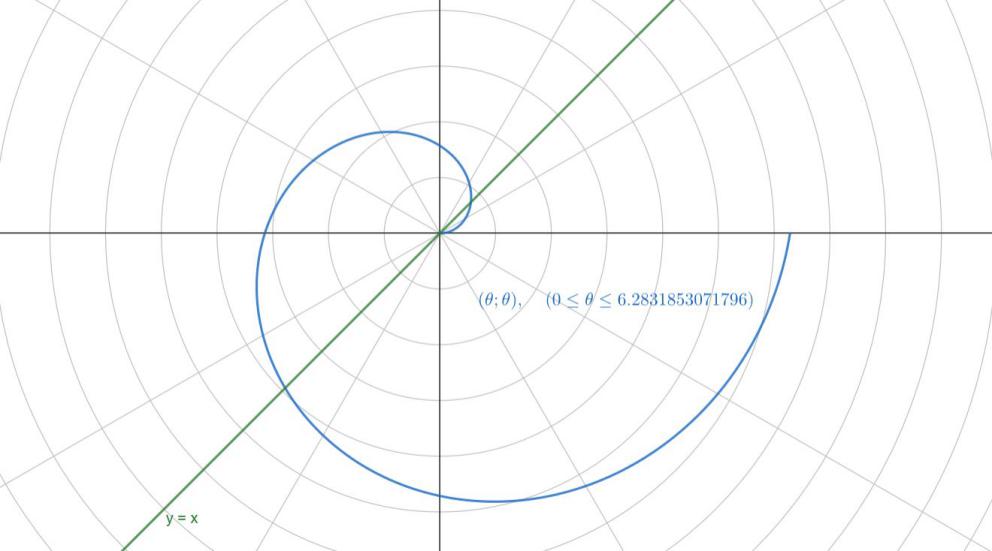
蓝色便是我们所熟知的“阿基米德螺线”。由于y=x直线与阿基米德螺线在表达式上的一致性，我们可以认为：阿基米德螺线是在极坐标系这种“扭曲”的平面（二维）空间中的“直线”。

4.空间直角坐标系

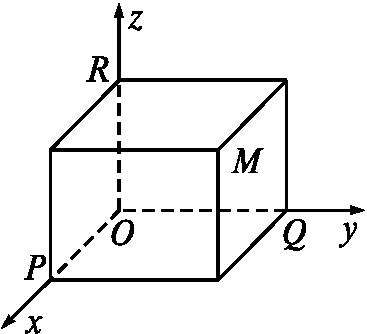
与平面直角坐标系类似，空间直角坐标系由空间中三个垂直的单位向量i=(1,0,0)，j=(0,1,0)，k=(0,0,1)构成。其他内容与平面直角坐标系基本相同，不再赘述。

5.柱坐标系

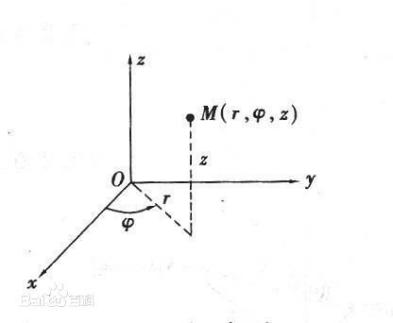
在了解了极坐标系以后，我们就可以很容易地理解柱坐标系了。

柱坐标系其实就是：z轴不变，将x轴、y轴构成的平面直角坐标系换成极坐标系。也就是说，柱坐标系中应该有两个坐标轴（上图不是很准确）——z轴与xOy平面的极轴。利用上面解释极坐标系的理论去解释就是：保留x轴与z轴，将y轴变换成在O处，xOy平面上的有向点圆，从而形成了柱坐标系。

6.球面坐标系

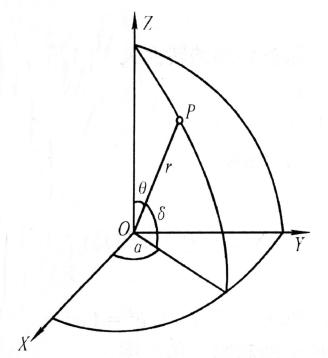
球面坐标系应当只有一个极轴（上图不准确）。这样想来，总有一种强烈的直觉告诉我们，球面坐标系似乎是由两个极坐标系构成的。是不是这样呢？

的确，球面坐标系由两个极坐标系构成，如下图：

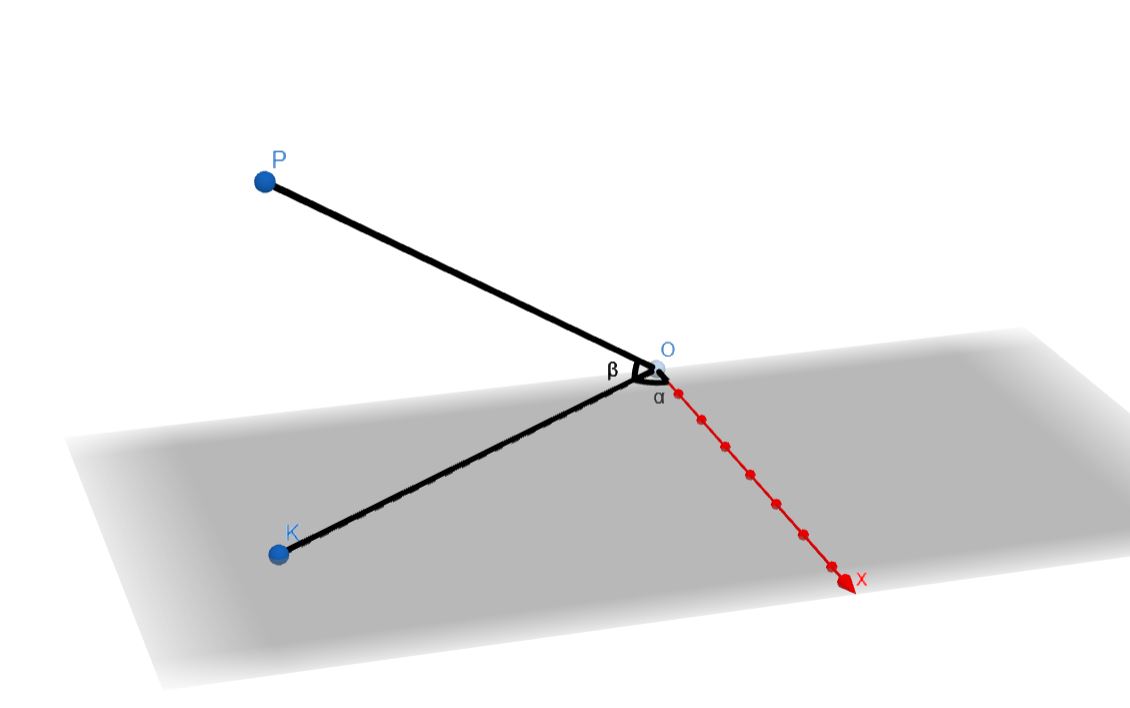
首先考虑xOy平面上的极坐标系。以O为极点，x轴为极轴，空间中点P在xOy平面上的投影为K，那么K就是xOy平面极坐标系中的一个点。为了确定P的位置，我们再以O为极点，以OK为极轴在垂直于xOy平面的平面上建立极坐标系，从而我们可以认为P是该系中的点。

综上所述，我们用两个极坐标系确定了点P的位置。与我们通常认知不同的是，第二个坐标系（OK系）可以认为是“动态”的，即随着P的运动，OK系可能同时发生运动，表现为K点的运动。

图形变换

图形变换中我们常见的有：平移变换，伸缩变换，对称变换，旋转变换等，对于前三者，尤其是前两者，大家可能都比较熟悉。因此对于前两者，我们重点介绍已有方法的本质性的原理，而对于后两者，我们以类似的原理来介绍变换的方法。

1. 平移变换

对于一个函数

，如果我们希望函数图像向右平移2个单位，得到的函数解析式应当是

，如果再向上平移2个单位，得到的函数解析式应当是

；这应给与中学老师所讲的“左加右减，上加下减”的口诀是对应的。

但是，在二维平面中，可以认为x轴与y轴的地位相同，即二者除了名称不同外其他性质基本一致。x轴向右是正方向，对应“减”；y轴向上是正方向，对应“加”。为什么同样是“正方向”，一个是“减”而另一个是“加”呢？这似乎与我们所说的x，y地位相同不甚符合。

上面的解析式

其实可以写成这个样子：

。这样我们便将正方向统一为了“减”；相对地，负方向也被统一为“加”。那么如果我们用二元方程

来表示平面曲线，那么

表示图像向右平移a个单位，向上平移b个单位。

那么为什么如何证明呢？

以x轴为例，y轴同理。如果我们记沿x轴正方向平移a个单位后的图像方程为

，对于其上任意一个点

，

为原图像

上的点，即

。也就是说，

。因此我们可以把平移后的图像方程表示为

。

2.伸缩变换

类似平移变换，

表示将图形

分别沿x轴、y轴伸长a，b倍。

证明过程与平移变换类似，读者可自行完成。

3.对称变换

对称变换我们无法给出一个确切的公式，但是可以给出一套比较成熟的算法。

如果原图像方程为

，要求其关于直线

的对称图像方程。

设对称后的方程为

，对于其上任意一个点

，存在

与

关于

对称，而

在原图像上，即

。

也就是说，对于

上任意一个点

，可以用

表示

，而

满足

，那么，

就是我们要求的方程了。

上述思想与前面给出的平移变换的证明思想基本相同。设出我们要求的方程，再根据某种变换规则找到原方程上对应的点，带入原方程得到答案。

4.旋转变换

旋转变换的思路与平移变换一致。

前面我们说过，平面直角坐标系中有方形网格，而极坐标系中有圆形网格；平面直角坐标系中的“阿基米德螺线”可以认为是极坐标空间中的“直线”。同样地，平面直角坐标系中的水平直线在极坐标空间下应当是一个圆，即圆可以认为是极坐标空间下的“与y轴平行的直线”。那么类似地，我们所说的旋转就可以认为是极坐标空间下的某种“平移”。

上面的描述过于抽象，我们还是考虑方程

，现要将其以原点为中心，逆时针旋转

。

高中我们都学过如何把一个平面直角坐标系下的方程用极坐标表示，方法在此不再赘述。如果我们得到对应的极坐标系下的方程是

，按照我们原有的想法，逆时针旋转

后的方程应当是

，因为逆时针是极坐标系中“y轴”的正方向。最后再把我们得到的极坐标方程变回直角坐标方程就可以了。

由此我们可以通过旋转变换证明函数

的图像是双曲线，并可以找到其焦点。具体过程留给感兴趣的朋友们自行完成。

总结

至此，我们讨论了坐标系的变换以及图形的变换，并且建立了不同种坐标系之间的关联，也建立了不同图形变换之间的关联。

其实数学的学习很多时候就是这样，先去思考一个事物的本质，从本质出发进行推广与关联，从而将原本看似“杂乱”的知识点融为一体。相似、相近知识点的学习大致会经历这么几个过程：

• 初次学习，感觉到有些杂乱，甚至搞不清楚它们之间的区别；
• 课后梳理，分清楚它们的区别点；
• 深入思考，发掘本质，寻找它们的共同点，从本质出发进行“关联”；
• 融汇贯通，不再有意区分这些知识点，因为你已经找到了它们共同的本质与根源。

上述过程在大学微积分中的六种积分（二重积分，三重积分，第一、二类曲线积分，第一、二类曲面积分）上体现得比较明显，具体内容将在日后的推文中阐述。

说明

本人非数学专业，上述内容仅为笔者个人的做题体验与总结，如有不完善、不严谨之处还请读者朋友们批评指正。