一、拉氏变换
matlab自带工具:拉氏变换(laplace)
例laplace(f)返回f的拉普拉斯变换。 默认情况下,自变量是t,变换变量是s。
例laplace(f,transVar)使用转换变量transVar而不是s(自定义变换变量)。
例laplace(f,var,transVar)使用自变量var和变换变量transVar分别代替t和s。
%% 拉式变换
clc
clear
syms s t
y=exp(-t)*cos(t); %原函数
LY=laplace(y) %拉氏变换
L_1=ilaplace(LY) %拉氏逆变换
e=L_1-y %做差检查结果是否正确
subplot(1,2,1)
fplot(y);%原函数图像
title("原函数图像")
legend("原函数")
subplot(1,2,2)
fplot(LY)%象函数图像
title("象函数图像")
legend("象函数")
clc
clear
syms w s c
F=w^2/(s*(s+c*w)^2);
f=ilaplace(F);
simplify(f);
二、传递函数模型
%% 传递函数模型实例
%例一
%G(s)=(12*s+15)/(s^3+16*s^2+64*s+192)
num=[12 15];
den=[1 16 64 192];
G=tf(num,den)
nyquist(G)
%例二
%G(s)=10*(2*s+1)/s^2*(s^2+7*s+13)
%方式1
num=conv(10,[2,1]);%计算分子多项式
den=conv([1 0 0],[1 7 13]);%计算分母多项式
G=tf(num,den)%求系统传递函数
%方式2
s=tf('s') %定义laplace算子
G=10*(2*s+1)/s^2/(s^2+7*s+13)% 直接给出系统传递函数表达式
%% 零极点增益模型
%G(s)=4*(s+5)^2/(s+1)(s+2)(s+2+2*j)(s+2-2*j)
%方式1:
z1=[-5;-5];
p1=[-1;-2;-2-2*j;-2+2*j];
k=4;
G1=zpk(z1,p1,k)
%方式2:
%G(s)=3*s^2+2*s+8/(s^4+3*s^3+8*s^2+4*s+2)
num=[3 2 8];
den=[1 3 8 4 2];
G=tf(num,den)
G1=zpk(G);%化为零极点增益形式
z=roots(num) %将G1零点存入z
p=roots(den) %将G1极点点存入p
pzmap(G1); %绘制零极点图
grid on %打开绘图网络三、nyquist和bode图

%% nyquist 和 bode 图
clc
clear
s=tf('s');
G=16/((s+6)*(s-1)); %系统开环传递函数
figure(1)
subplot(3,2,1)
nyquist(G)
title("系统开环传递函数nyquist图")
subplot(3,2,2)
bode(G)
title("系统开环传递函数bode图")
Gk=G/(1+G); %系统闭环传递函数
subplot(3,2,3)
nyquist(Gk)
title("系统闭环传递函数nyquist图")
subplot(3,2,4)
bode(Gk)
title("系统闭环传递函数bode图")
Y1=Gk/s%单位阶跃响应
subplot(3,2,[5 6])
nyquist(Y1)
title("单位阶跃响应(增加开环极点P=2)")
% [h,r,wg,wc]=margin(G) %求系统的频率特性参数
%h幅值裕量
%相角裕量
%wg幅值穿越频率
%相位穿越频率
figure(2)
G1=16/((s+6)*(s-1)*(s-2)); %增加开环极点P=2
subplot(3,2,1)
nyquist(G1)
title("系统开环传递函数nyquist图(增加开环极点P=2)")
subplot(3,2,2)
bode(G1)
title("系统开环传递函数bode图")
Gb=G1/(1+G1); %系统闭环传递函数
subplot(3,2,3)
nyquist(Gb)
title("系统闭环传递函数nyquist图(增加开环极点P=2)")
subplot(3,2,4)
bode(Gb)
title("系统闭环传递函数bode图")
Y=Gb/s%单位阶跃响应
subplot(3,2,[5 6])
nyquist(Y)
title("单位阶跃响应(增加开环极点P=2)")运行结果
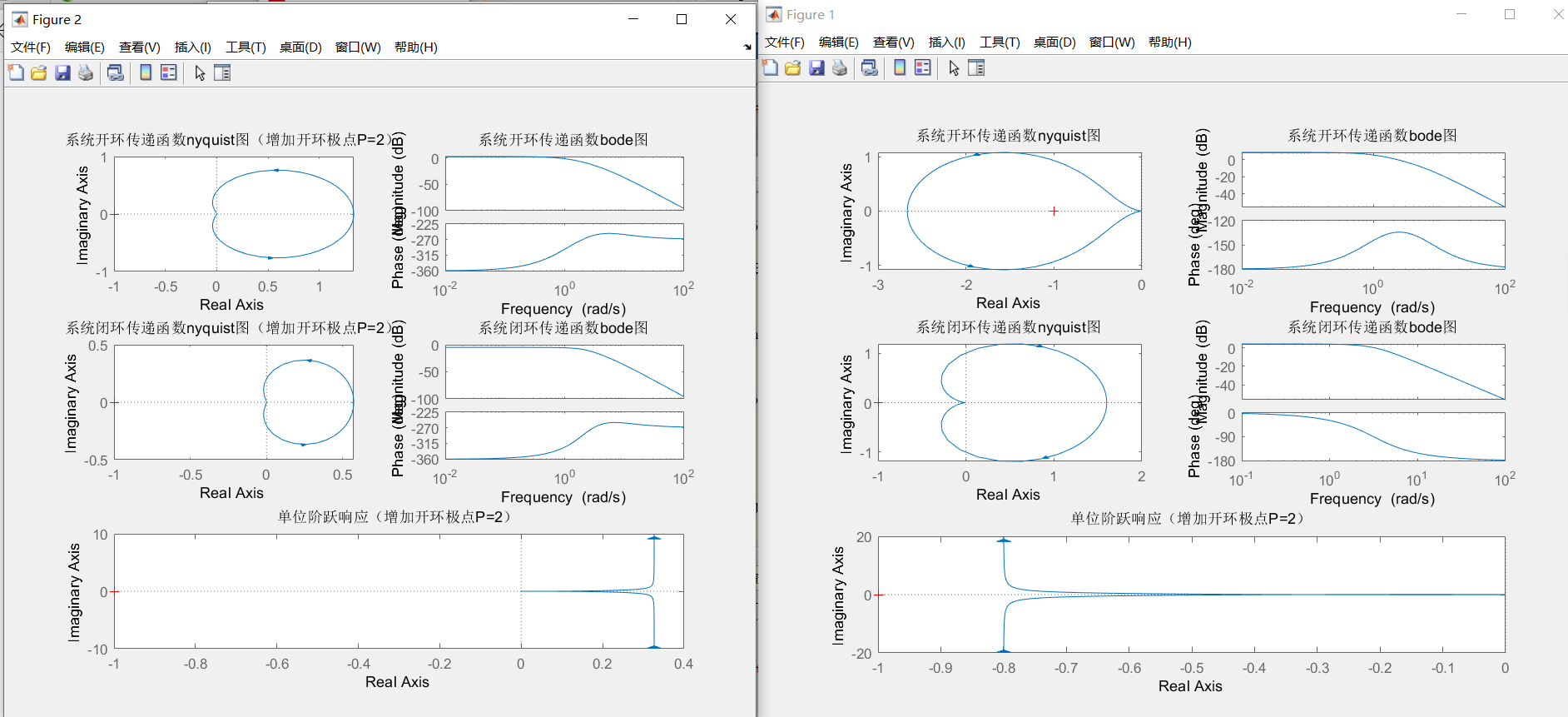
最后
以上就是英俊黑猫最近收集整理的关于MATLAB之Nyquist图和Bode图一、拉氏变换二、传递函数模型三、nyquist和bode图的全部内容,更多相关MATLAB之Nyquist图和Bode图一、拉氏变换二、传递函数模型三、nyquist和bode图内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复