试画出下面系统的乃式图
题目: G ( s ) = 1 s 2 ( s + 1 ) ( 2 s + 1 ) G(s)=frac{1}{s^2(s+1)(2s+1)} G(s)=s2(s+1)(2s+1)1
1. 正常的解题
G ( s ) = 1 s 2 ( s + 1 ) ( 2 s + 1 ) G(s)=frac{1}{s^2(s+1)(2s+1)} G(s)=s2(s+1)(2s+1)1
解:
第一步:
G
(
j
ω
)
=
1
(
j
ω
)
2
(
j
ω
+
1
)
(
2
j
ω
+
1
)
=
−
1
ω
∗
1
ω
∗
1
j
ω
+
1
∗
1
2
j
ω
+
1
=
1
ω
2
∗
ω
2
+
1
∗
(
2
ω
)
2
+
1
e
−
π
2
−
π
2
−
a
r
c
t
a
n
ω
−
a
r
c
t
a
n
2
ω
=
1
ω
2
∗
ω
2
+
1
∗
(
2
ω
)
2
+
1
e
−
π
−
a
r
c
t
a
n
ω
−
a
r
c
t
a
n
2
ω
G(jω)=frac{1}{(jω)^2(jω+1)(2jω+1)}=-frac{1}{ω}*frac{1}{ω}*frac{1}{jω+1}*frac{1}{2jω+1}=frac{1}{ω^2*sqrt{ω^2+1}*sqrt{(2ω)^2+1}}e^{-frac{π}{2}-frac{π}{2}-arctanω-arctan2ω}=frac{1}{ω^2*sqrt{ω^2+1}*sqrt{(2ω)^2+1}}e^{-π-arctanω-arctan2ω}
G(jω)=(jω)2(jω+1)(2jω+1)1=−ω1∗ω1∗jω+11∗2jω+11=ω2∗ω2+1∗(2ω)2+11e−2π−2π−arctanω−arctan2ω=ω2∗ω2+1∗(2ω)2+11e−π−arctanω−arctan2ω
∴
∣
G
(
j
ω
)
∣
=
1
ω
2
∗
ω
2
+
1
∗
(
2
ω
)
2
+
1
therefore|G(jω)|=frac{1}{ω^2*sqrt{ω^2+1}*sqrt{(2ω)^2+1}}
∴∣G(jω)∣=ω2∗ω2+1∗(2ω)2+11
∠
G
(
j
ω
)
=
−
π
−
a
r
c
t
a
n
ω
−
a
r
c
t
a
n
2
ω
angle{G(jω)}=-π-arctanω-arctan2ω
∠G(jω)=−π−arctanω−arctan2ω
第二步:
① 当 ω = 0 时,A(ω) = ∞,φ(ω) = -π;
② 当 ω = 0 时,A(ω) = 0,φ(ω) = -2π;
第三步:
再求与正虚轴的交点
∠
G
(
j
ω
)
=
−
π
−
a
r
c
t
a
n
ω
−
a
r
c
t
a
n
2
ω
=
−
3
2
π
angle{G(jω)}=-π-arctanω-arctan2ω=-frac{3}{2}π
∠G(jω)=−π−arctanω−arctan2ω=−23π
ω
=
1
2
ω=sqrt{frac{1}{2}}
ω=21
∴
∣
G
(
j
1
2
)
∣
=
1
(
1
2
)
2
∗
(
1
2
)
2
+
1
∗
(
2
(
1
2
)
)
2
+
1
=
0.94
therefore|G(jsqrt{frac{1}{2}})|=frac{1}{(sqrt{frac{1}{2}})^2*sqrt{(sqrt{frac{1}{2}})^2+1}*sqrt{(2(sqrt{frac{1}{2}}))^2+1}}=0.94
∴∣G(j21)∣=(21)2∗(21)2+1∗(2(21))2+11=0.94

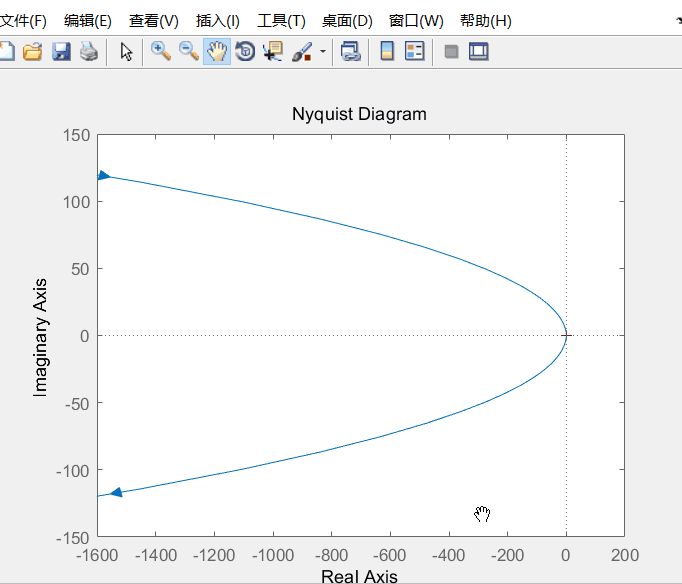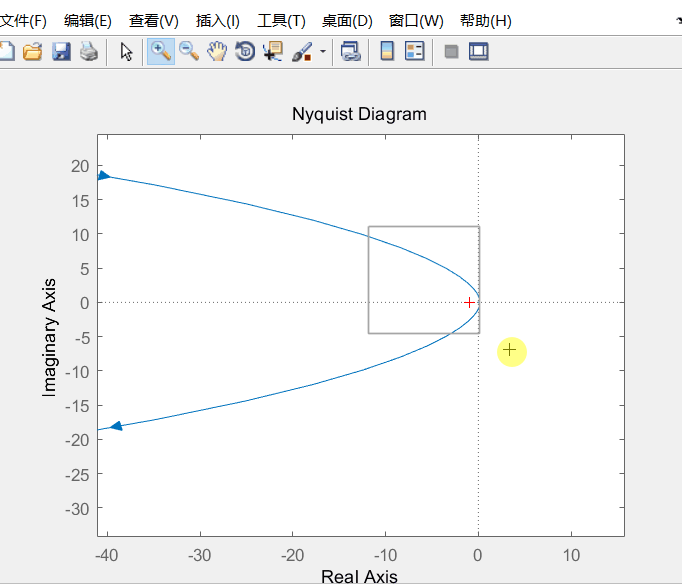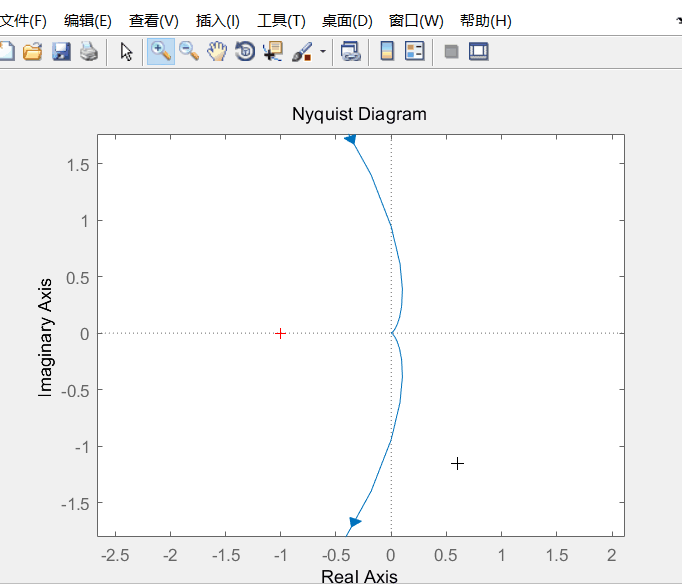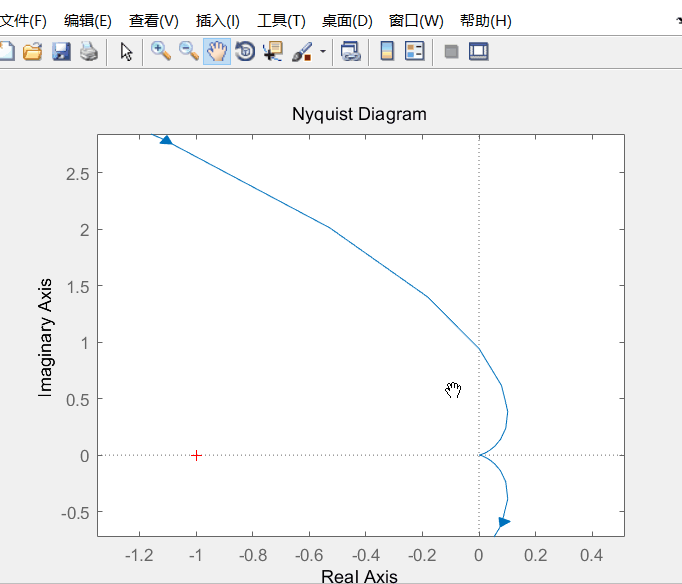
2. Matlab求证
s=tf('s');
g = 1/(s^2*(s+1)*(2*s+1));
nyquist(g)
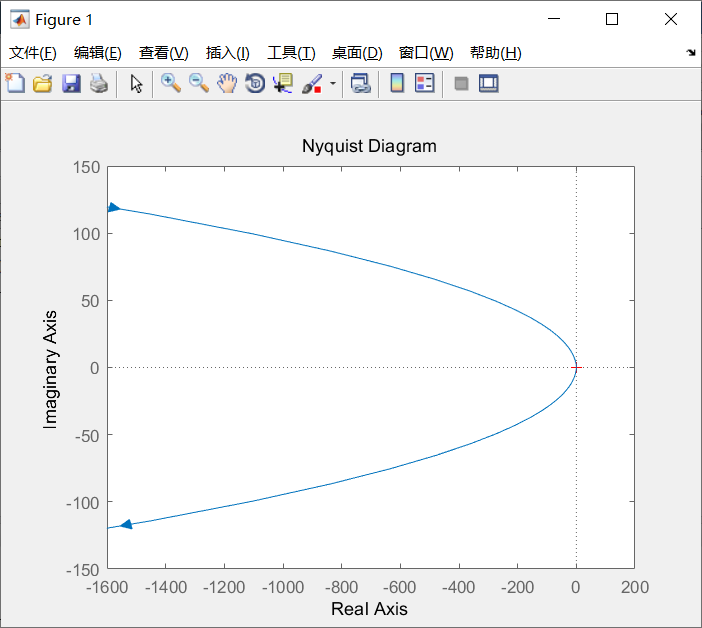
这里就要疑问了,嗯???,为什么我画的图与Matlab里的不一样呢?
实际上需要放大:
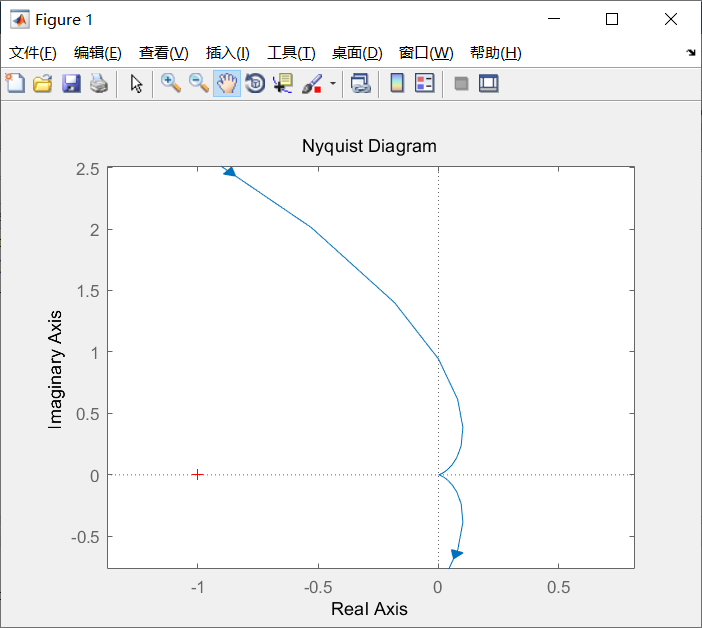
附一张 GIF:
点我回顶部 ☚
Fin.
最后
以上就是知性毛衣最近收集整理的关于试画出下面系统的乃式图(nyquist图)【Matlab】点我回顶部 ☚的全部内容,更多相关试画出下面系统的乃式图(nyquist图)【Matlab】点我回顶部内容请搜索靠谱客的其他文章。








发表评论 取消回复