注:读书笔记中只摘录了部分知识点,不是全书内容的梳理
全书划分为3个部分:
- 第 1-4 章:主要介绍图神经网络所需的基础知识,包括图的基本概念、卷积神经网络以及表示学习
- 第 5-9 章:主要介绍图卷积神经网络理论基础和性质、图神经网络的各种变体和框架范式、图分类以及基于GNN的图表示学习
- 第 10 章:图神经网络目前的应用
第一章 图的概述
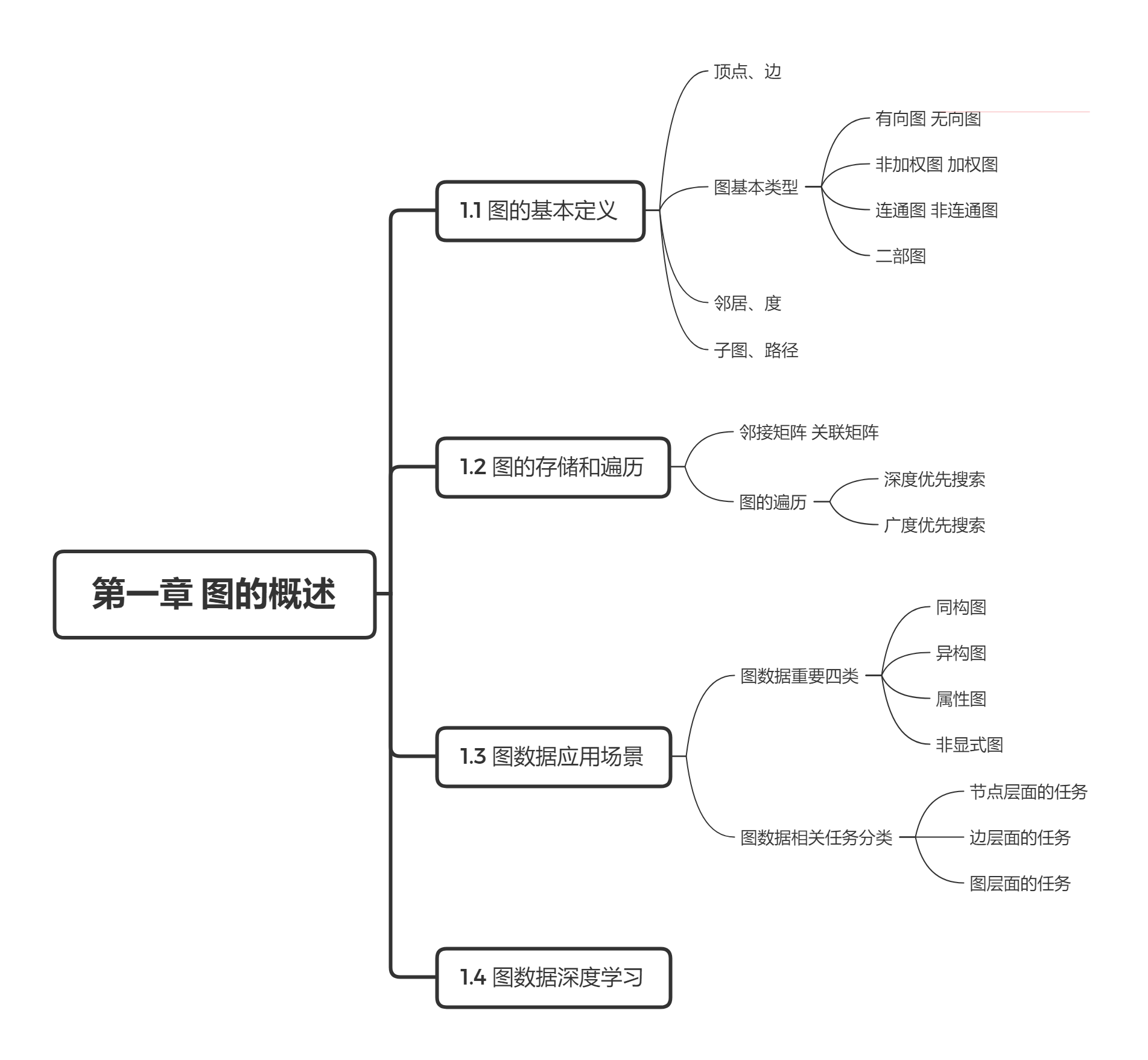
1.1 图的基本定义
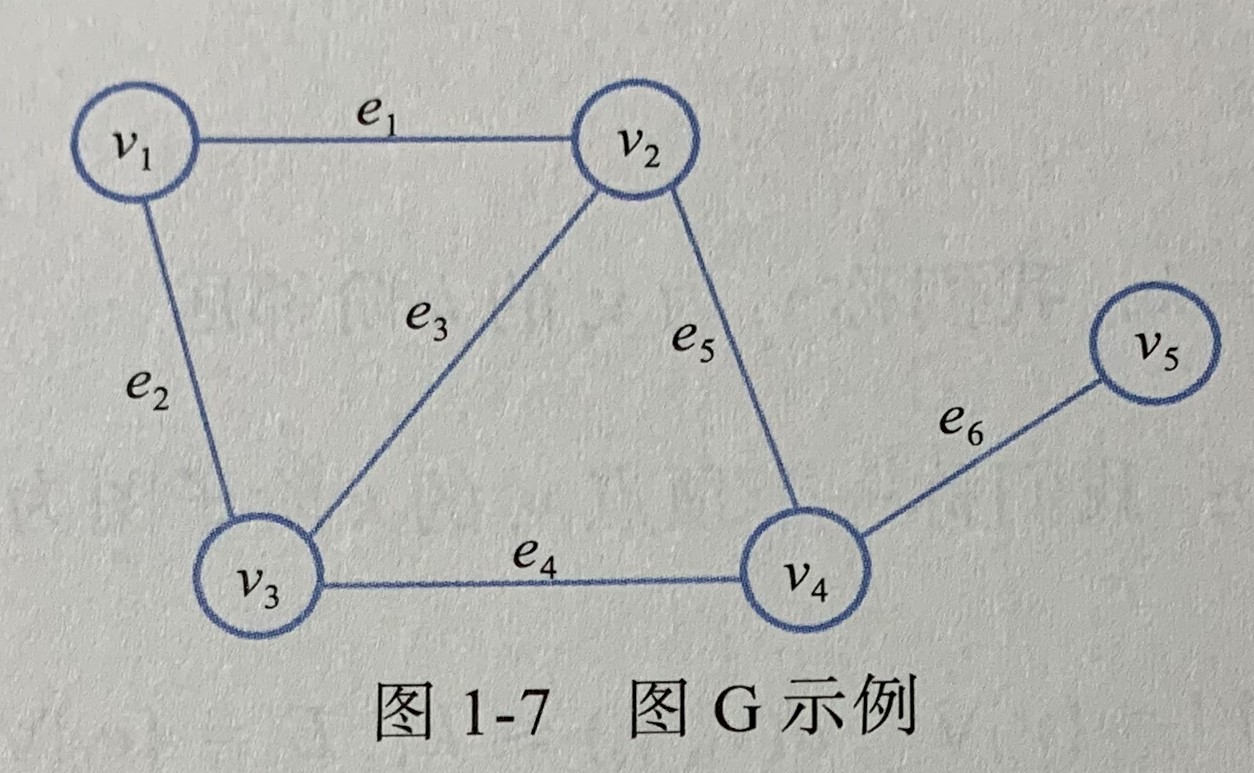
- 图 由顶点(vertex) 和边(edge) 构成,顶点表示研究对象,边表示两个对象之间特定的关系。图可表示为顶点和边的集合,记为 G = ( V , E ) G = (V, E) G=(V,E)
- 两个顶点之间的距离 由它们的最短路径的长度决定
1.2 图的存储和遍历
- 邻接矩阵 A A A 描述图中顶点之间的关联
- 关联矩阵
B
B
B 描述节点和边之间的关联
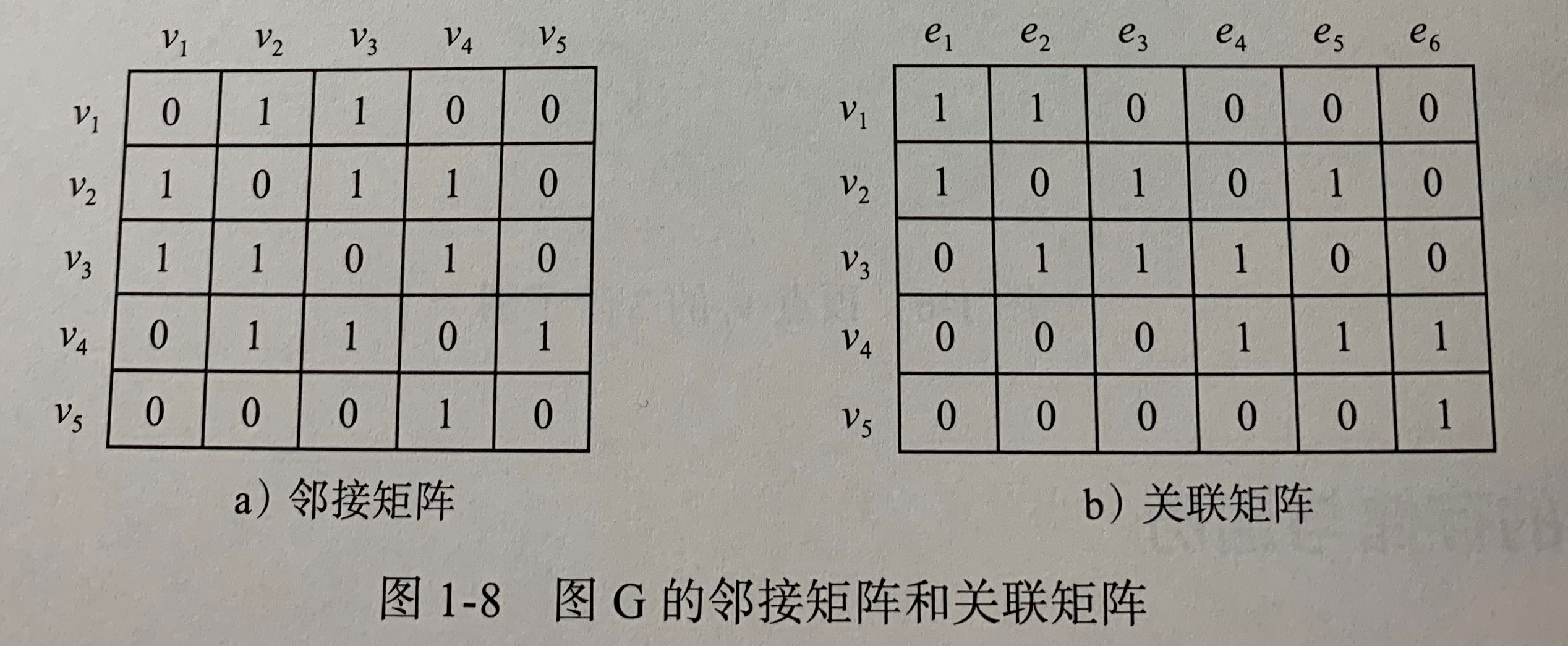
图的遍历 指从途中的某一顶点出发,按照某种搜索算法沿着图中的边对图中所有顶点访问一次且只访问一次
- 深度优先搜索,是一个递归算法,有回退过程
- 广度优先搜索,是一个分层搜索过程,没有退回过程
1.3 图数据应用场景
| 图数据类型 | 特点 | 举例 |
|---|---|---|
| 同构图 | 图中的节点类型和关系类型都仅有一种,一般用来研究用户的重要性排名以及相关的用户推荐等问题 | 如在线社交网络的用户关注网络,用户为节点,用户之间的关注关系为边 |
| 异构图 | 图中的节点类型或关系类型多于一种,能够完成更加多样化的任务 | 如将更多元化的媒体对象补充进社交网络中 |
| 属性图 | 给图数据增加额外的属性信息,广泛适用于多种业务场景下的数据表达 | 如节点和关系都有标签和属性 |
| 非显式图 | 数据之间没有显示地定义出关系,需要先依据规则/计算方式将数据关系表达出来,再将数据当成一种图数据研究 | 如计算机3D视觉中的点云数据,可以将空间距离转化为关系,这样一来点云数据就变成了图数据 |
| 图数据任务 | |
|---|---|
| 节点层面 | 主要包括分类任务和回归任务,如用户标签分类 |
| 边层面 | 主要包括边的分类和检测任务,如将用户视为节点,将用户之间的关注关系视为边,通过边预测实现社交用户的推荐 |
| 图层面 | 从图的整体结构出发,实现分类、表示和生成等任务,如药物分子的分类 |
1.4 图数据深度学习
《 A new model for learning in graph domains 》
- 首次提出图神经网络概念,使得学习过程可直接架构于图数据之上
《 Neural Network for Graphs: A Contextual Constructive Approach 》
《 The graph neural network model 》
- 进一步阐述图神经网络
- 提出一种监督学习的方法训练GNN
- 但是缺点是早期提出的计算方式消耗非常大
《 Spectral Networks and Locally Connected Networks on Graphs 》
- 首次将卷积引入图神经网络中,基于频域卷积操作的概念开发了一种图卷积网络模型
- 首次将可学习的卷积操作用于图数据之上
- 基于频谱卷积的方法,计算时需要同时处理整个图,时间复杂度高,难以扩展到大规模图数据的学习任务上。所以,基于空域的图卷积被提出并开始流行
《 Semi-Supervised Classification with Graph Convolutional Networks 》
- 将频谱图卷积的定义进行简化,使图卷积操作能够在空域进行,极大提高计算效率
《 Inductive Representation Learning in Large Attributed Graphs 》
《 Graph Attention Networks 》
《 Neural Message Passing for Quantum Chemistry 》
《 Image Generation from Scene Graphs 》
- 基于空域图卷积神经网络模型的变体
- 加强了学习系统对各类图数据的适应性
第二章 神经网络基础(略)
第三章 卷积神经网络
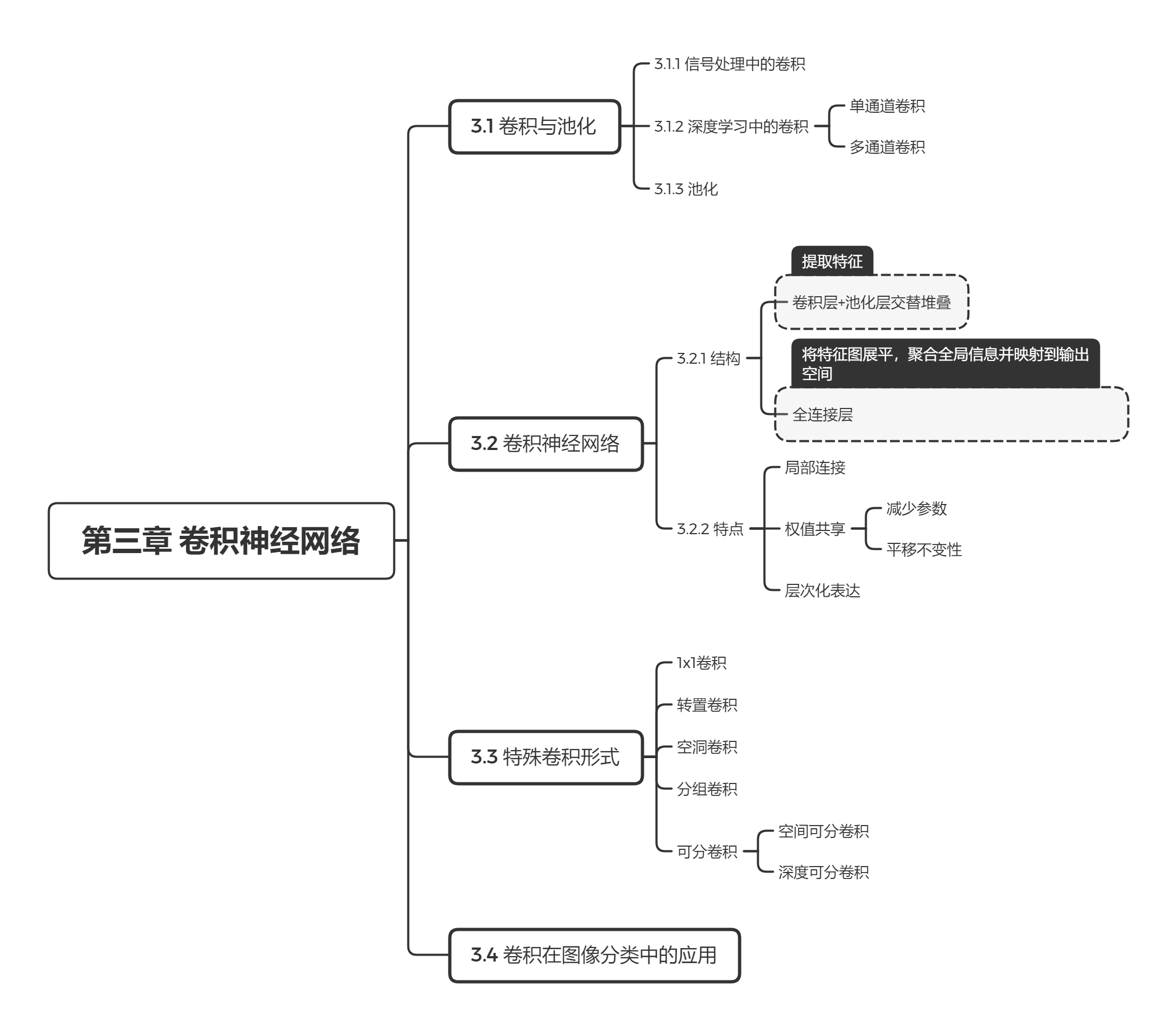
知识点1:多通道卷积
- 输入层和卷积核有相同的深度
- 卷积核只在高和宽两个方向上移动(所以这种操作也称为2D卷积),此处要注意区分3D卷积
- 最后得到的是单通道输出
知识点2:平移不变性
指的是,当对左右两只眼睛提取特征时,使用相同的卷积核,能得到相同的输出
知识点3:空间可分卷积
一文读懂 12种卷积方法(含1x1卷积、转置卷积和深度可分离卷积等)
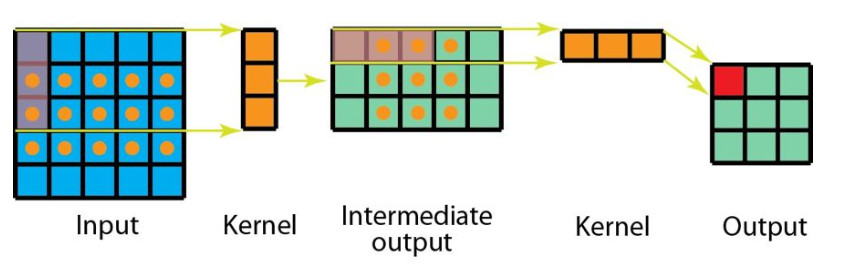
- 将一个卷积分解为两个独立的运算,例如可以将3x3的卷积核分成一个3x1核和1x3核
- 乘法次数更少,更节省成本
知识点4:深度可分卷积
问题1 :如何通过2D卷积操作,使空间维度(高度/宽度)变小,深度增大?
-
输入:7x7x3;卷积核:3×3×3;输出:5×5×1
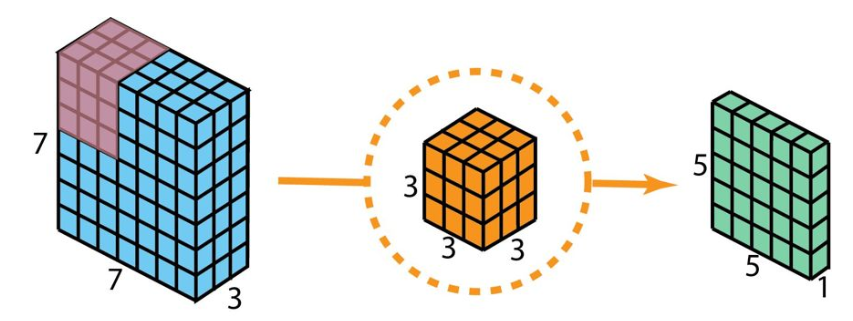
-
当使用128个卷积核,就可以使深度增加
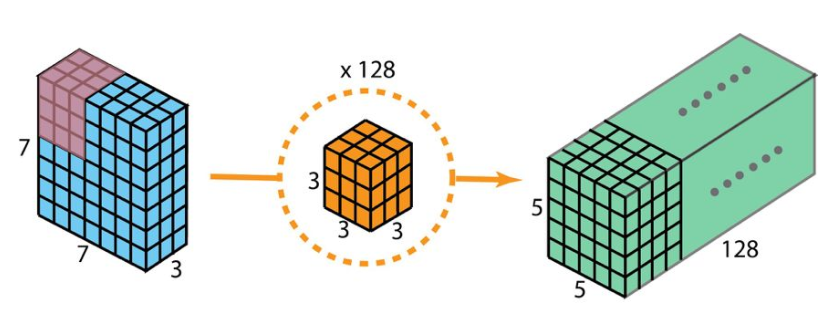
该步骤中,每个3×3×3核移动5x5次,共128 x 3 x 3 x 3 x 5 x 5 = 86400 次乘法
问题2 :如何通过深度可分卷积操作,使空间维度(高度/宽度)变小,深度增大?
- 将前文提到的3×3×3卷积核分开,变成3个核,每个核3×3×1。**然后,每个核与输入层的一个通道卷积,注意,是一对一关系。**于是每次卷积得到5×5×1输出,将输出堆叠到一起,得到5×5×3的输出。
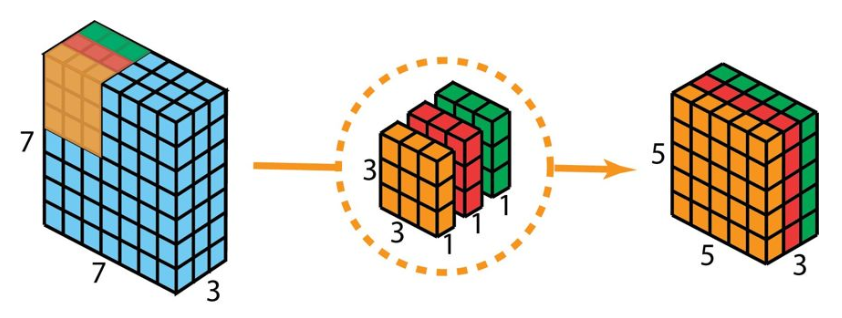
该步骤中,3个3×3×1移动5×5 次,共3 x 3 x 3 x 1 x 5 x 5 = 675 次乘法 - 为了扩展深度,再应用128个形状为1x1x3的卷积核,这样就能得到5x5x128的输出
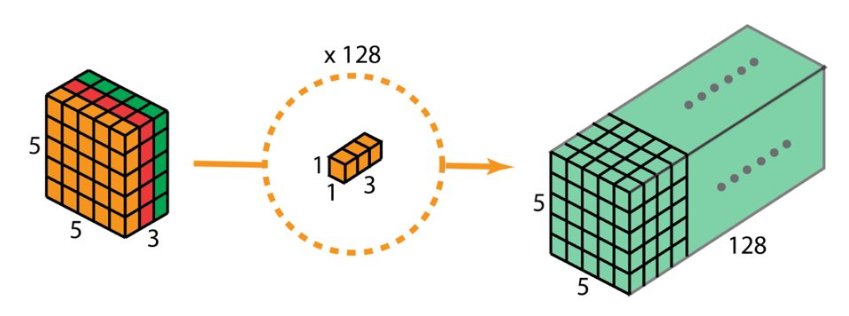
该步骤中,每个核移动5×5 次,128个核移动128 x 1 x 1 x 3 x 5 x 5 = 9600 次乘法
即,深度可分卷积成本要远远低于2D卷积,因此该方法常常应用于对速度有要求的结构设计中。
第四章 表示学习
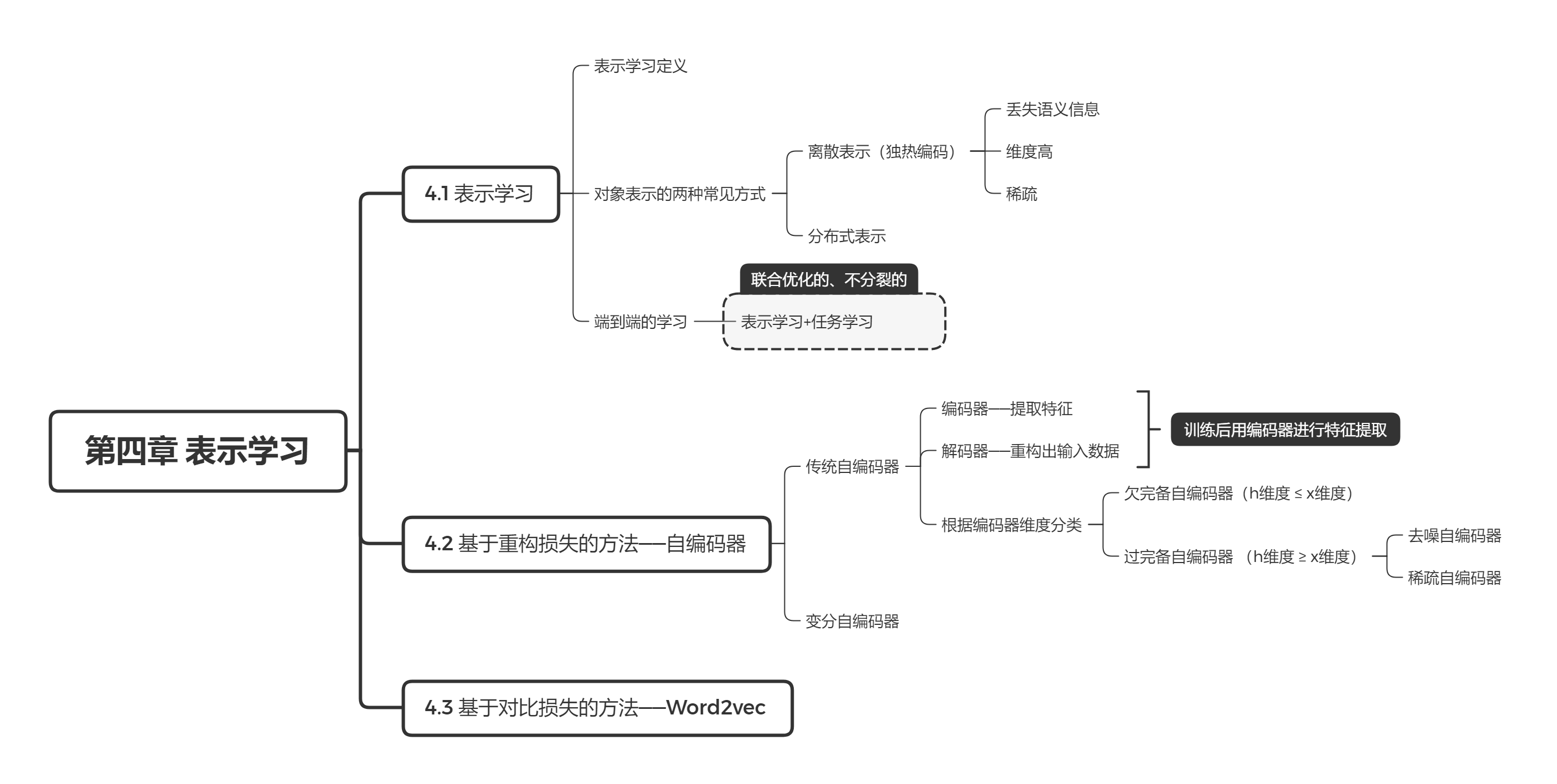
知识点1:表示学习 通常是学习一种映射关系,即将输入映射到一个稠密的低维向量空间中。
知识点2:过完备自编码器
- 编码器维度上不加以限制,有可能不会学习到数据的任何有用信息,而仅仅是将输入复制到输出。原因在于,维度不加以限制,自编码器会倾向于直接将输入拷贝为输出,而不会从数据中提取到有价值的特征。
- 基于该种情况,常常会对模型进行一些正则化约束
最后
以上就是超级指甲油最近收集整理的关于读书笔记《深入浅出图神经网络》 Part 1第一章 图的概述第二章 神经网络基础(略)第三章 卷积神经网络第四章 表示学习的全部内容,更多相关读书笔记《深入浅出图神经网络》内容请搜索靠谱客的其他文章。








发表评论 取消回复