信道容量2

几种概率：

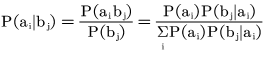
目录

一：信道的基本概念

                         信道的分类

                         信道的数学模型

                         单符号离散信源 

                          信道疑义度 

                         平均互信息的物理意义

                        条件互信息 

 二：信道容量及其计算

                  1：特殊信道

                  2：离散对称信道的信道容量

                          对称离散信道的性质

                           准对称信道

                          对称信道的通解 

                  3：一般信道容量的求解

一：信道的基本概念

信道的分类

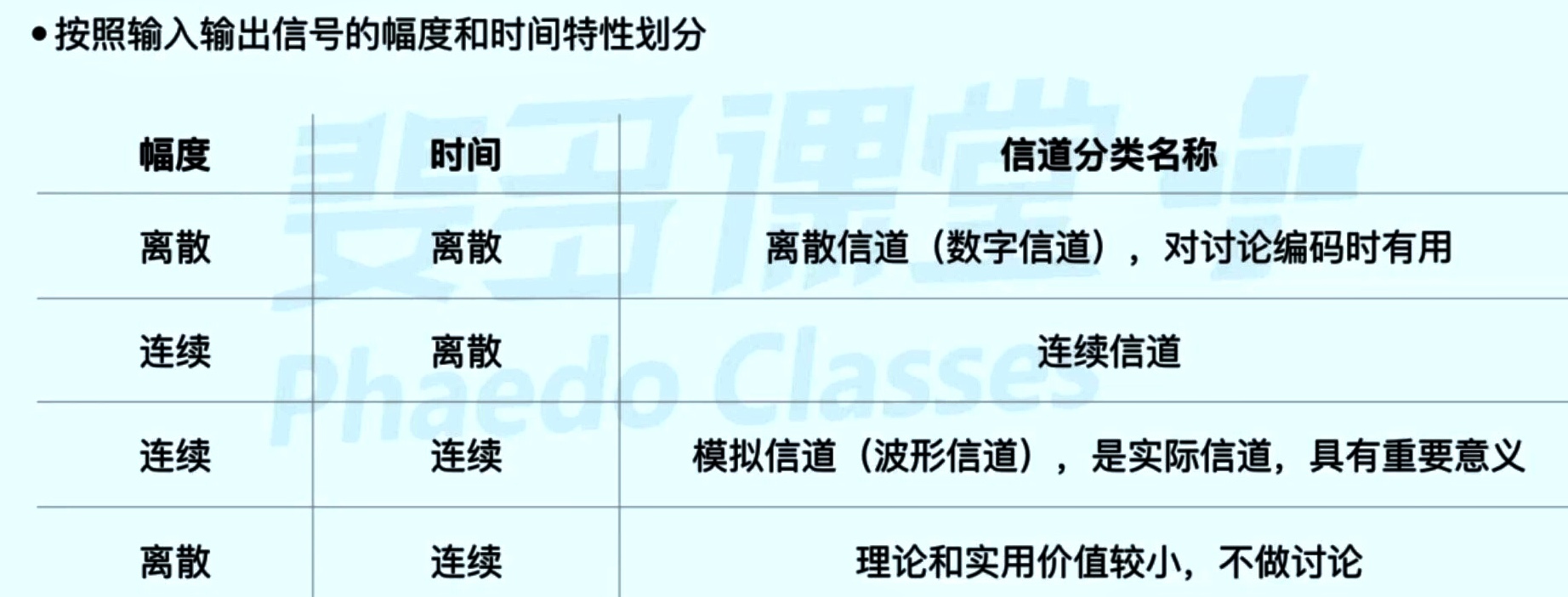
注：对模拟信道（波形信道）进行采样就可以得到：连续信道

 信道的数学模型

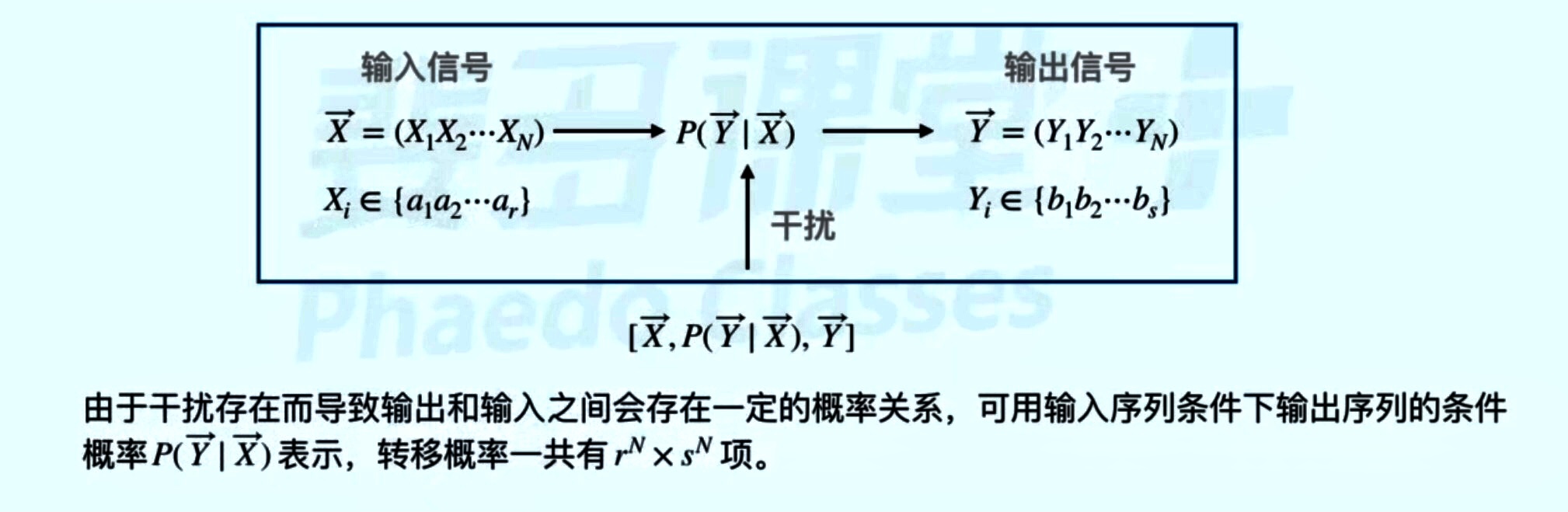
具体信道：

单符号离散信源 

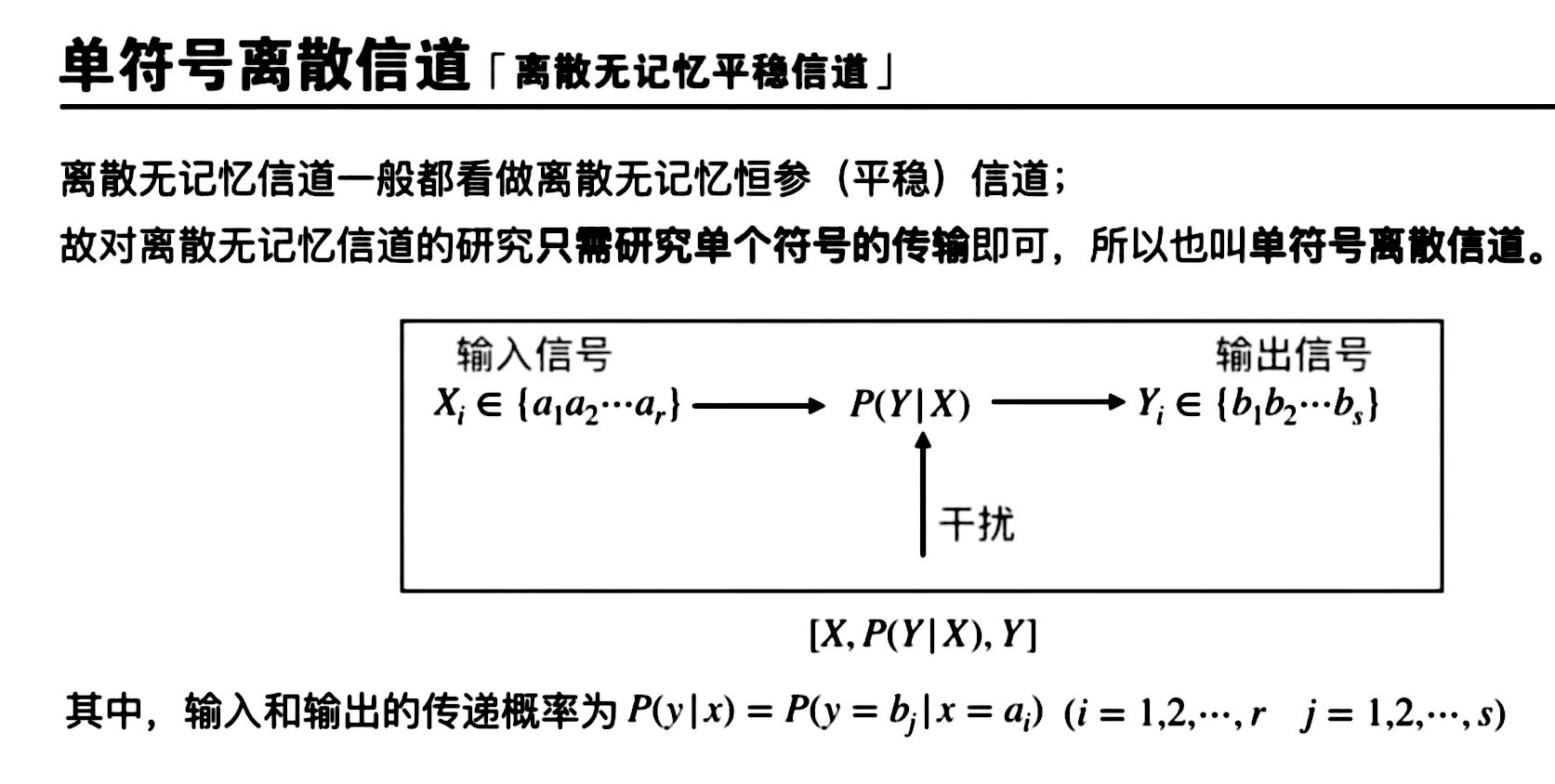
信道疑义度 

习题：计算互信息

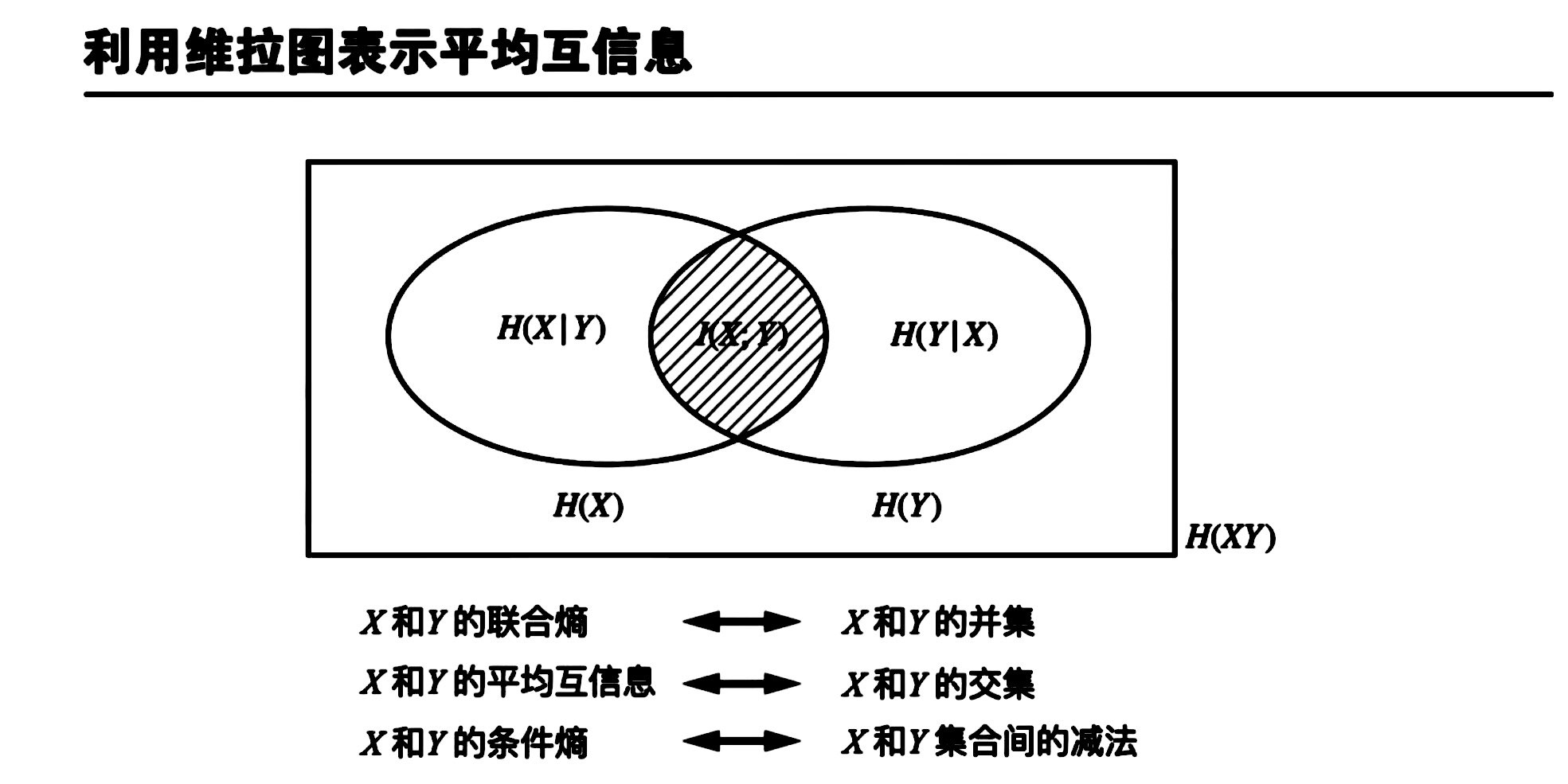
平均互信息的物理意义

1：

H(X|Y):信道疑义度/损失熵/后验熵，收到输出后对输入仍存在的不确定性
H(X)：X的先验不确定性/先验熵/无条件熵
I(X,Y):从Y中获得的X的信息量，x不确定性的减少量

2：

H(Y|X):噪声熵，发出x之后，对y存在的平均不确定度 ，噪声引起的（已知输入对输出的不确定）

:3：

 I(X,Y):输出前后的不确定性的减少量。
H(X)+H(Y):输入前X和Y视为相互独立的随机变量，系统的先验熵是两者之和。
H(XY):X和Y实际输出过程中，信道的作用使两者的关联。

习题：平均互信息计算 

条件互信息 

1：联合互信息量

2:平均联合互信息

3:条件互信息
给定y求x和z的互信息

 4：平均条件互信息

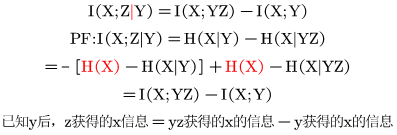
 二：信道容量及其计算

信息传输率:   R=I(X,Y)
物理意义：接收Y后平均每个符号获得的关于X的信息量=平均每个符号发送的信息量
信道容量：在最佳输入分布（信道容量达最大值时的输入分布）时，最大信息传输率的值。
信道容量与输入分布无关，是个值，只是这个值会在最佳输入分部时取得。

1：特殊信道

特点：输出只能来源一个输入，已知输出后输入没有不确定了（H(X|Y)=0）。 

2：离散对称信道的信道容量

离散对称信道 
          若一个离散无记忆信道的信道矩阵中，每一行或每一列都由其他行或其他列同一组元素的不同排列，则称此信道为：离散对称信道。
         识别时：行------第一行{}的置换；列-----第一列{}的置换。
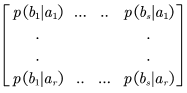s种输入，r种输出。
强对称信道：（均匀信道）

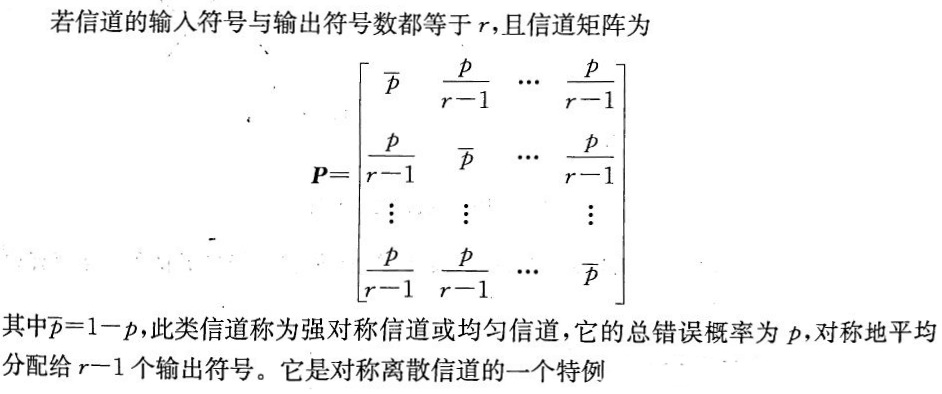
 正确输出p补全部在对角线上。

对称离散信道的性质

1：H(Y|X)=(s种输出,P的某一行的s种符号组成的熵)

2:当P(X)等概输入，输出也是等概分布。（输入等概，输出等概）

发现：每个p(y)值相等
由1和2去求信道容量C

对于均匀信道的C: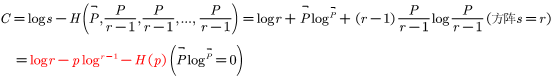

BSC:二元对称信道 r=2  C=log2-H(P).

离散对称信道习题

准对称信道

求解公式：

 准对称信道：划分的子集都是对称信道，子集两两不相交，并起来为：信道矩阵

对称信道的通解 

原理：达到信道容量对应的最佳输入分布是等概分布。直接利用等概分布去求。
C=H(Y)-H(Y|X)

3：一般信道容量的求解

信道容量求解的本质：多元函数在约束条件下求极值问题。
约束条件：,输入和输出符号是多个体现了：多元。
一般采用拉格朗日乘子法：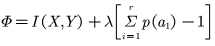

TH:

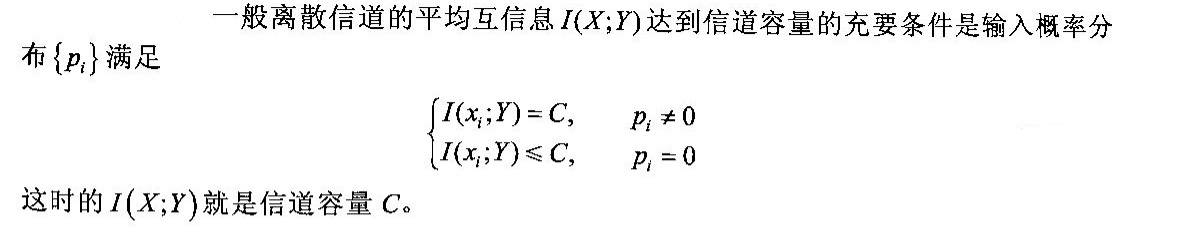
解释：
如果每一个概率不为0的输入符号与输出符号集合的互信息相同，且概率为0的输入符号与输出符号集合的互信息小于上述不为0的，那么这种概率分布就是最佳输入分布，从而I(X,Y)达到最大值。

最后

以上就是听话台灯为你收集整理的信道容量2的全部内容，希望文章能够帮你解决信道容量2所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。