目录
- 无线信道
- 有线信道
- 信道的顺序额模型
- 调制信道模型
- 编码信道模型
- 用转移概率描述编码信道的特性,二进制系统中,错误概率为0变1和1变0的概率之和 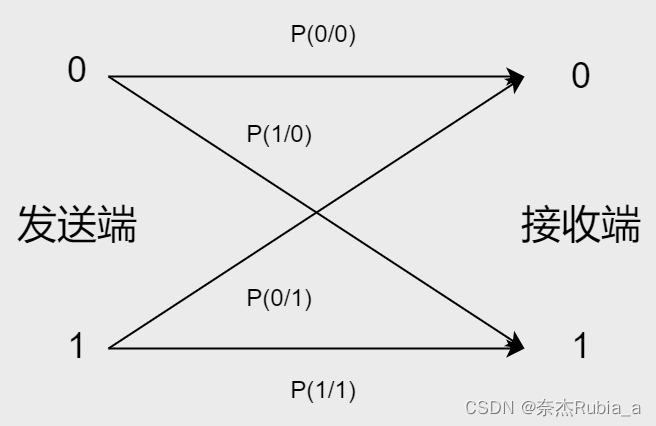
- 信道容量
- 离散信道容量
- 连续信道容量
无线信道
- 地波:频率低于2MHz,可以沿着弯曲的地表传播,拥有一定绕射能力,传输距离超过数百甚至数千千米
- 天波:频率大于2MHz小于30MHz,通过地球的电离层多次反射传输,传输距离通常大于10000千米以上,电磁波不能到达的区域称为寂静区
- 视线:频率大于30MHz,电磁波穿透电离层,无法被反射回来,则需要架设收发天线。我们设地球半径为r(km),天线之间的距离为D(km),架设高度为h(m),则有:
h = D 2 8 r ≈ D 2 50 ( m ) h=frac{D^2}{8r} approx frac{D^2}{50} qquad(m) h=8rD2≈50D2(m)
卫星通信其实就相当于一个非常高的信号塔,只需要少量卫星就可以完成全球的信号传输
而电磁波在大气中传播会受到大气影响,频率越高信号衰减越严重
电磁波还可以通过散射传播
- 电离层散射:发生在30MHz到60MHz的电磁波上,由于电离层的不均匀性
- 对流层散射:大气不均匀产生,发生在100MHz到4000MHz电磁波,传递距离大约为600千米
- 流行余迹散射:流行经过大气层产生的强电离余迹产生的散射,频率在30MHz到100MHz之间,传播距离达到1000千米以上
有线信道
- 明线:架设在电线杆上的架空线路
- 对称电缆:由若干对芯线的双导线放在一根保护套制成
- 同轴线缆:内外两根同心圆柱导体构成
信道的顺序额模型
调制信道模型
最基本的调制信道可表示为:
e
o
(
t
)
=
f
[
e
i
(
t
)
]
+
n
(
t
)
e_o(t)=f[ei(t)]+n(t)
eo(t)=f[ei(t)]+n(t)
其中
e
o
(
t
)
、
e
i
(
t
)
e_o(t)、e_i(t)
eo(t)、ei(t)分别为输出端和输入端电压,
n
(
t
)
n(t)
n(t)为噪声电压,无论是否有信号噪声总是存在,所以称为加性噪声或加性干扰,上式子可改写为:
e
o
(
t
)
=
k
(
t
)
e
i
(
t
)
+
n
(
t
)
e_o(t)=k(t)e_i(t)+n(t)
eo(t)=k(t)ei(t)+n(t)
k
(
t
)
k(t)
k(t)可看作一种乘性干扰,如果
k
(
t
)
k(t)
k(t)随时间变化,则为时变信道,如果
k
(
t
)
k(t)
k(t)随机变化称为随参信号,
k
(
t
)
k(t)
k(t)变化较小甚至不变化则称为恒参信号。
编码信道模型
用转移概率描述编码信道的特性,二进制系统中,错误概率为0变1和1变0的概率之和

信道容量
通信传输过程即为减少不确定的过程
离散信道容量
离散信道容量有两种不同的度量单位,这两者之间是等价的,可以根据情况选用
- 每个符号到能够传输的平均信息量最大值表示信道容量 C C C
- 单位时间内能够传输的平均信息量最大值表示信道容量
C
t
C_t
Ct
C = max P ( x ) [ H ( x ) − H ( x / y ) ] ( b / 符 号 ) C t = max P ( x ) { r [ H ( x ) − H ( x / y ) ] } ( b / s ) C= mathop{max}_{P(x)}[H(x)-H(x/y)]qquad(b/符号) \ \ C_t= mathop{max}_{P(x)}{r[H(x)-H(x/y)]} qquad(b/s) C=maxP(x)[H(x)−H(x/y)](b/符号)Ct=maxP(x){r[H(x)−H(x/y)]}(b/s)
其中:
H ( x ) = − ∑ i = 1 n P ( x i ) log 2 P ( x i ) H ( x / y ) = − ∑ j = 1 m P ( y j ) ∑ i = 1 n P ( x i / y j ) log 2 P ( x i / y j ) H(x)=-sum_{i = 1}^{n}P(x_i)log_2P(x_i)\ \ H(x/y)=-sum_{j = 1}^{m}P(y_j)sum_{i = 1}^{n}P(x_i/y_j) log_2P(x_i/y_j) H(x)=−i=1∑nP(xi)log2P(xi)H(x/y)=−j=1∑mP(yj)i=1∑nP(xi/yj)log2P(xi/yj)
贝叶斯公式:
P ( x i / y j ) = P ( x i ) P ( y j / x i ) ∑ i = 1 n P ( x i ) P ( y j / x i ) P(x_i/y_j)=frac{P(x_i)P(y_j/x_i)}{sum_{i = 1}^{n}P(x_i)P(y_j/x_i)} P(xi/yj)=∑i=1nP(xi)P(yj/xi)P(xi)P(yj/xi)
连续信道容量
对于带宽有限、平均功率有限的高斯白噪声连续信道,可以证明信道容量为香农公式:
C
t
=
B
log
2
(
1
+
S
N
)
=
B
log
2
(
1
+
S
n
0
B
)
(
b
/
s
)
C_t=Blog_2left( 1+frac{S}{N} right)= Blog_2left( 1+frac{S}{n_0B} right) qquad(b/s)
Ct=Blog2(1+NS)=Blog2(1+n0BS)(b/s)
其中S为信号平均功率,N为噪声功率,B为带宽,
n
0
n_0
n0为噪声单边功率谱密度
对于极限情况:
{
S
→
∞
C
t
→
∞
n
0
→
0
C
t
→
∞
B
→
∞
C
t
→
2
S
2
n
0
left{ begin{aligned} Stoinfty&qquad C_ttoinfty\ n_0to 0&qquad C_ttoinfty\ Btoinfty&qquad C_ttofrac{sqrt{2}S}{2n_0} end{aligned} right.
⎩⎪⎪⎪⎨⎪⎪⎪⎧S→∞n0→0B→∞Ct→∞Ct→∞Ct→2n02S
最后
以上就是喜悦彩虹最近收集整理的关于【通信原理】四、信道无线信道有线信道信道的顺序额模型信道容量的全部内容,更多相关【通信原理】四、信道无线信道有线信道信道内容请搜索靠谱客的其他文章。








发表评论 取消回复