希尔伯特变换分析及应用

概述

希尔伯特变换是信号处理中一种常用的手段。常常用来作为信号的相位调整手段，但每次变换只能相位偏移90°。且希尔伯特变换只能近似应用于窄带信号。对于任意给定$t$时刻，通过希尔伯特变换运算后的结果只能存在一个频率值，即只能处理任何时刻为单一频率的信号。对于一个非平稳的数据序列，希尔伯特变换得到的结果很大程度上失真，所以应用希尔伯特变换要特别谨慎。

正文

数学定义是：

设有一个实函数$X(t)$，其希尔伯特变换记作$\hat{X}(t)$（或记作$H\left[X(t)\right]$）

$\hat{X}(t)=H\left[X(t)\right]=\frac{1}{\pi }{\int }_{-\infty }^{\infty }\frac{X(\tau )}{t-\tau }d\tau$

反变换为：

$X(t)=H^{-1}\left[\hat{X}(t)\right]=-\frac{1}{\pi }{\int }_{-\infty }^{\infty }\frac{\hat{X}(\tau )}{t-\tau }d\tau$

与卷积的概念相比较，可以发现，上面的Hilbert变换的表达式实际上就是将原始信号和一个信号做卷积的结果。这个用来卷积的信号就是$h(t)=\frac{1}{\pi t}$

所以对$h(t)$做$FFT$可以得到：

H ( j w ) = F { h } ( w ) = − j s g n ( w ) H(jw)=F{h}(w)=-jsgn(w) H(jw)=F{h}(w)=−jsgn(w)

或者

$sgn(w)=\left\{\begin{array}{c}1,w>0\\ 0,w=0\\ -1,w<0\end{array}\right\}$

其中$F$是傅里叶变换，$j$是虚数单位，$w$是频率。

从频域上看，$sgn(w)$即将原始信号的正频率部分乘以$-j$，负频率部分乘以$j$，也就是说，在保持幅度不变的情况下，可以将信号正频率部分相位偏移$-\frac{\pi }{2}$，负频率相位偏移$\frac{\pi }{2}$。

所以希尔伯特转换步骤为：

(1)将原始信号进行傅里叶变换

(2)将转换后的信号分为正频率部分和负频率部分，正频率信号数据**{ 将虚部数据换到实部，将实部数据乘以-1换到虚部}，负频率信号数据{将虚部数据乘以-1换到实部，将实部数据换到虚部}**

(3)将交换后的数据进行傅里叶反变换得到最终结果

如下图所示：

实验结果

本实验基于STM32F429，移植ARM_DSP库，使用实数fft变换函数。

C代码参考：

arm_rfft_fast_init_f32(&S, TEST_LENGTH_SAMPLES);
for(i=0; i<1024; i++)
{
testInput_f32[i] = sin(2*3.1415926f*50*i/1024);
}
//正变换
ifftFlag = 0;
arm_rfft_fast_f32(&S, testInput_f32, testOutput_f32, ifftFlag);
for(i=0; i<512; i++)
{
fft_tmp.real[i] = testOutput_f32[2*i];
fft_tmp.ima[i] = testOutput_f32[2*i + 1];
}
//hilbert 
for(i=0;i<512;i++)
{
hilbert_tmp.real[i] = fft_tmp.ima[i];
hilbert_tmp.ima[i] = -fft_tmp.real[i];
}
for(i=0;i<512;i++)
{
testInput_f32[2*i] = hilbert_tmp.real[i];
testInput_f32[2*i + 1] = hilbert_tmp.ima[i];
}
//反变换
ifftFlag = 1;
arm_rfft_fast_f32(&S, testInput_f32, fft_iout, ifftFlag);

由于点数太多，所以仅显示250个点。实验结果如下：

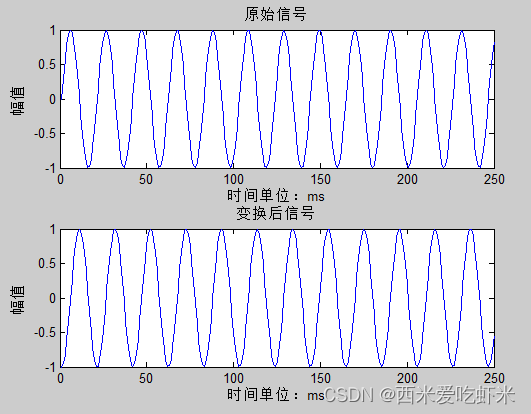
总结

这样就完成了希尔伯特变换在信号处理上的应用。

最后

以上就是鲤鱼黑夜为你收集整理的希尔伯特变换分析及应用的全部内容，希望文章能够帮你解决希尔伯特变换分析及应用所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。