1.掌握求解LMI的目的(以及整套流程)
掌握matlab中LMI工具箱的函数使用
2.掌握schurs补
--------------------------------------------------
你的点赞是我更新的动力!
--------------------------------------------------
一.掌握求解LMI的目的(以及整套流程)
掌握matlab中LMI工具箱的函数使用
1.首先初始化
setlmis([])
%注意这只是定义了一个矩阵不等式系统,并没有定义矩阵
2.定义矩阵变量
limvar(在LMI问题中指定矩阵变量)函数,函数格式
X = lmivar(type,struct)type为矩阵格式
type = 1 为对角块对称矩阵格式,每个对角块都是全矩阵(任意对称矩阵),标量(单位矩阵的倍数)或相同的零。
type = 2 为m*n任意矩阵格 struct =[m n]
struct定义对角块矩阵的格式,
如有r个对角块,struct就是r x 2为的矩阵。
eg:X0 = limvar(1,[2 1;1 0]) ,[2 1]表示2x2的满阵,[1 0]表示1x1的标量
参考:https://blog.csdn.net/weixin_44051006/article/details/99754816
3.定义矩阵不等式
lmiterm([第几个不等式矩阵 行坐标 列坐标 要求的未知矩阵] , 左乘矩阵,右乘矩阵,'s'是否对称转置);
注意:
所有的工具箱中始终以‘<’ 小于号来计算lmiterm项(不是用‘>’ 大于号来计算)
小于号左边标记为正号,小于号右边为负号
eg1.1.
S>I 在工具箱中的表示代码为:
(要将大于号换成小于号,即表示为I<S)
lmiterm([3,1,1,0],1)%为正3
lmiterm([-3,1,1,S],1,1)%为负3
eg1.2.
4.实战写代码
eg.1:
出个题,按照下面给出的参数,在matlab中用工具箱搭建出相对应的代码
(先自己思考,再看答案掌握更加深刻)

其中:alpha=0.2;
beta=sqrt(alpha*(1-delta));

答案:(下面附上本例子的代码。)
function [Q1,K]=LMI_learning0()
clc;
close all;
clear all;
%{
程序功能:求解LMI可行解
2022.2.17
%}
%% 参数初始化
rho=0.9;
delta=0.0526;
alpha=0.2;
beta=sqrt(alpha*(1-delta));
A=[-1 3.5;-0.8 -0.5];
B=[-1 1;2 -1];
C=[1 -1;1 -1];
D=[-0.12 0.2;0.1 -0.1];
E=[-0.21 2.5;0.2 -0.3];
t=1;
Ft=diag([sin(t),cos(t)]);%对角矩阵
M1=D*Ft*E;
M2=B-D*Ft*E
u=alpha*(1-delta)
v=-beta*(1-beta)
w=(1-alpha)*(1-delta)
%% 描述矩阵不等式
%初始化LMI
setlmis([]);
%定义变量
n=2;
Q1=lmivar(1,[n,1]);%1表示为对角矩阵
[2,1]表示二阶满块矩阵
K=lmivar(1,[n,1]);
%逐个描述矩阵中每一个单元
lmiterm([1,1,1,Q1],-1,1)
%第(一行二列)的0矩阵不需要写就是0矩阵
lmiterm([1,1,3,0],A')%第(一行三列)的加法要分开算
%0表示外部变量
lmiterm([1,1,3,-K],u,M1')%-K表示转置
lmiterm([1,1,4,-K],v,M1')
lmiterm([1,2,2,0],-1)%表示单位矩阵I
lmiterm([1,2,3,-K],w,M2')
lmiterm([1,2,4,-K],-v,M2')
lmiterm([1,3,3,inv(Q1)],-1,1)
lmiterm([1,4,4,inv(Q1)],-1,1)
%另外两个矩阵表示Q1>0,K>0,(即为正定矩阵)
%也即0<Q1 , 0<K
lmiterm([-2,1,1,Q1],1,1)
lmiterm([-3,1,1,K],1,1)
lmisys=getlmis;%获取LMI信息
%% 求解LMI
[tmin,xfeas]=feasp(lmisys);%用feasp求解器求解
if(tmin<0)%小于0才有解
disp('feasible!!!!!!!!!!!!!');
Q1=dec2mat(lmisys,xfeas,Q1);%将Q1转换成可以识别的mat类型
K=dec2mat(lmisys,xfeas,K);
else
Q1=nan;
K=nan;
end
end参考:鲁棒控制理论(一)LMI矩阵不等式 - 知乎
鲁棒控制理论(二)LMI矩阵不等式工具箱 - 知乎
Matlab和控制理论(八)线性矩阵不等式LMI工具箱的使用_哔哩哔哩_bilibili
eg2.
主要看代码中的注释即可
Je=0.9145;
Jp=0.0364;
Kf=0.1188;
La=0.66;
Lh=0.178;
A=[0 0 1 0;
0 0 0 1;
0 0 0 0;
0 0 0 0];
B=[0 0;
0 0;
(Kf*La)/Je (Kf*La)/Je;
(Kf*Lh)/Jp -(Kf*Lh)/Jp];
C=[1 0 0 0;0 1 0 0];
N=[C;C*A];
M=[B A*B];
n=rank(N)
m=rank(M)
alpha=-10;
r=5;
setlmis([])
P=lmivar(1,[4 1]);%P为4*4
W=lmivar(2,[4 2]);%W为4*2
%%
lmiterm( [1 1 1 P],1,A,'s');%PA+A.T*P
lmiterm( [1 1 1 W],-1,C,'s');%-WC-C.T*W.T
%{
矩阵为
[
PA+A.T*P-WC-C.T*W.T<0
]
%}
lmiterm([ 2 1 1 P] , -1, 1);%-P
lmiterm([ 2 1 2 P] , 1, A);%PA
lmiterm([ 2 1 2 W] , -1, C);%-WC
lmiterm([ 2 1 2 P] , -alpha, 1);%-alpha*P
lmiterm([ 2 2 2 P] , -r^2, 1);%-r^2*P
%{
矩阵为
[
-P , PA-WC--alpha*P;
<0
0
, -r^2*P
]
%}
%%
lmisys=getlmis;
[tmin,xfeas]=feasp(lmisys);
P=dec2mat(lmisys,xfeas,P);
W=dec2mat(lmisys,xfeas,W);
L=pinv(P)*W二.掌握schurs补
1.先讲一下下面的方法容易记住

2.再讲schur补的详细数学证明:(参考《鲁棒控制》——俞立 著)


3.举个例子
eg.如果想要下列不等式转换为线性矩阵不等式怎么办?(先自己思考,再看答案掌握更加深刻)
其中
思路:在matlab的LMI工具箱只能解”矩阵不等式“,所以要将上述不等式转化为”矩阵不等式“才可以用工具箱求解,用一个谚语来形容更好理解——换汤不换药(同样的不等式,只不过换成了矩阵形式)
解:(我自己写了一下,打字太麻烦,字丑见谅)
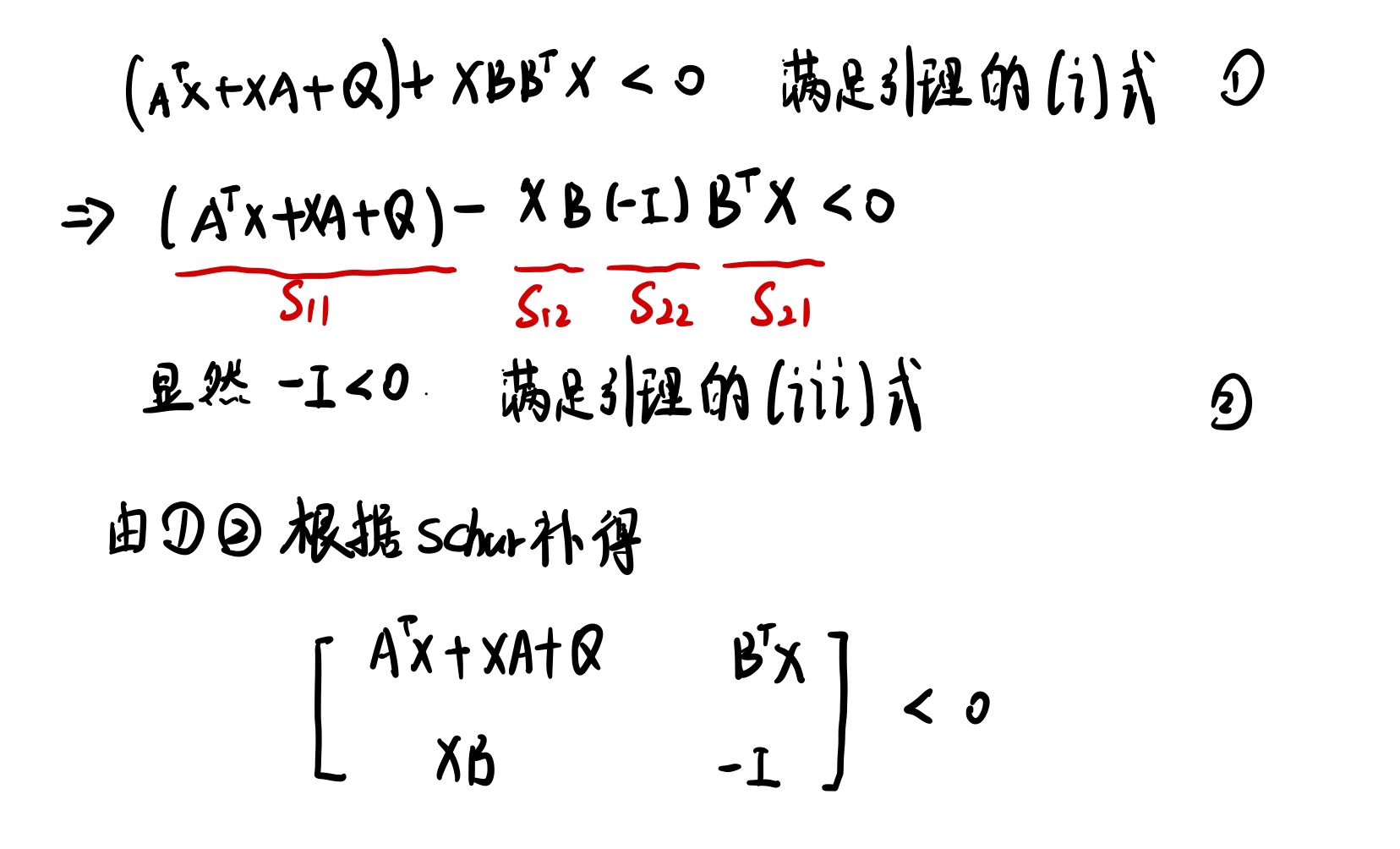
参考:2021-05-19 Schur补引理及证明_你这瓜保熟吗-CSDN博客_schur补引理
舒尔补/schur补_颹蕭蕭-CSDN博客_舒尔补引理矩阵小于0
matlab里LMI工具问题,如何根据schur补性质等价成矩阵不等式 – MATLAB中文论坛
Matlab中的LMI工具箱的研究与使用
(1161条消息) 矩阵的舒尔补(Schur complement)_百把人的博客-CSDN博客_舒尔补
最后
以上就是灵巧星星最近收集整理的关于LMI(线性矩阵不等式)、schur补 学习笔记一.掌握求解LMI的目的(以及整套流程) 掌握matlab中LMI工具箱的函数使用二.掌握schurs补的全部内容,更多相关LMI(线性矩阵不等式)、schur补内容请搜索靠谱客的其他文章。









发表评论 取消回复