执行下列指令,观察其运算结果, 理解其意义:
(1) [1 2;3 4]+10-2i
(2) [1 2; 3 4].*[0.1 0.2; 0.3 0.4]
(3) [1 2; 3 4].[20 10;9 2]
(4) [1 2; 3 4].^2
(5) exp([1 2; 3 4])
(6)log([1 10 100])
(7)prod([1 2;3 4])
(8)[a,b]=min([10 20;30 4])
(9)abs([1 2;3 4]-pi)
(10) [10 20;30 40]>=[40,30;20 10]
(11)find([10 20;30 40]>=[40,30;20 10])
(12) [a,b]=find([10 20;30 40]>=[40,30;20 10]) (提示:a为行号,b为列号)
(13) all([1 2;3 4]>1)
(14) any([1 2;3 4]>1)
(15) linspace(3,4,5)
(16) A=[1 2;3 4];A(:,2)
1,矩阵各元素依次+10-2i
2,前者矩阵中的元素与后者矩阵中的元素按位置依次相乘,得到的结果将作为新矩阵中相同位置的元素。
3,A(前) 和 B(后) 的元素逐个对应相除:B(i,j)/A(i,j)两数组之间必须有相同的形,或其中一个是标量。
4,AB中的元素逐个进行如下运算:A(i,j)^B(i,j),A(i,j)/B(i,j)两数组之间必须有相同的形,或其中一个是标量。
5,等于[exp(1),exp(2);exp(3),exp(4)]
6,行向量各元素以e为底的对数
7,返回矩阵n的每列元素的乘积,结果是一个行向量(3=1*3, 8=2*4)
8, a为各列最小值,b为最小值所在的行号
9,返回矩阵每个元素取绝对值-π
10,矩阵每个对应位置元素做比较,返回0否,1是
(10>=40,false, 20>=30,false, 30>=20, ture, 40>=10,ture)
11,返回前矩阵>=后矩阵项的序数
结果表明编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)
12,返回前矩阵>=后矩阵项的位置(a行数,b列数)
编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)
13,该矩阵每列是否全>1
14,该矩阵每列是否存在<1的数
(all, any都是按列运算)
15,返回起始点为3,终止点为4,元素个数为5的等差数列
(将区间[3,4]分隔成5维等距向量,即5-1=4等分)
16,返回第二列所有项
执行下列指令,观察其运算结果、变量类型和字节数,理解其意义:
(1) clear; a=1,b=num2str(a),c=a>0, a==b, a==c, b==c
(2) clear; fun='abs(x)',x=-2,eval(fun),double(fun)
(1)
1,返回值:1,1,1,0,1,0。
a, b, c的值尽管都是1, 但数据类型分别为数值,字符, 逻辑
注意a与c相等, 但他们不等于b
(2)返回值:abs(x),-2, 2,
97 98 115 40 120 41
double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码
本金K以每年n次,每次p%的增值率(n与p的乘积为每年增值额的百分比)增加,当增加到rK时所花费的时间为
(单位:年)
用MATLAB表达式写出该公式并用下列数据计算:r=2, p=0.5, n=12.
>> r=2;p=0.5;n=12;
>> T=log(r)/n/log(1+0.01*p) %注意不能将log写成ln
T =
11.5813(1) 用z=magic(10)得到10阶魔方矩阵;
(2) 求z的各列元素之和;
(3) 求z的对角线元素之和(提示:先用diag(z)提取z的对角线);
(4) 将z的第二列除以根号3;
(5) 将z的第3行元素加到第8行。
>> z=magic(10)
z =
92
99
1
8
15
67
74
51
58
40
98
80
7
14
16
73
55
57
64
41
4
81
88
20
22
54
56
63
70
47
85
87
19
21
3
60
62
69
71
28
86
93
25
2
9
61
68
75
52
34
17
24
76
83
90
42
49
26
33
65
23
5
82
89
91
48
30
32
39
66
79
6
13
95
97
29
31
38
45
72
10
12
94
96
78
35
37
44
46
53
11
18
100
77
84
36
43
50
27
59
>> sum(z)
ans =
505
505
505
505
505
505
505
505
505
505
>> sum(diag(z)) //先用diag(z)提取z的对角线
ans =
505
>> z(:,2)/sqrt(3)
ans =
57.1577
46.1880
46.7654
50.2295
53.6936
13.8564
2.8868
3.4641
6.9282
10.3923
>> z(8,:)=z(8,:)+z(3,:)
z =
92
99
1
8
15
67
74
51
58
40
98
80
7
14
16
73
55
57
64
41
4
81
88
20
22
54
56
63
70
47
85
87
19
21
3
60
62
69
71
28
86
93
25
2
9
61
68
75
52
34
17
24
76
83
90
42
49
26
33
65
23
5
82
89
91
48
30
32
39
66
83
87
101
115
119
83
87
101
115
119
10
12
94
96
78
35
37
44
46
53
11
18
100
77
84
36
43
50
27
59已知函数
在(-2, 2)内有两个根。取步长h=0.05, 通过计算函数值求得函数的最小值点和两个根的近似解。(提示:求近似根等价于求函数绝对值的最小值点)
>> x=-2:0.05:2;f=x.^4-2.^x;
>> [fmin,min_index]=min(f)
fmin =
-1.3907
%最小值
min_index =
54
%最小值点编址
>> x(min_index)
ans =
0.6500
%最小值点
>> [f1,x1_index]=min(abs(f))
%求近似根--绝对值最小的点
f1 =
0.0328
x1_index =
24
>> x(x1_index)
ans =
-0.8500
>> x(x1_index)=[];f=x.^4-2.^x;
%删去绝对值最小的点以求函数绝对值次小的点
>> [f2,x2_index]=min(abs(f))
%求另一近似根--函数绝对值次小的点
f2 =
0.0630
x2_index =
65
>> x(x2_index)
ans =
1.2500最后
以上就是专一唇膏最近收集整理的关于DHU matlab experiment note<1>的全部内容,更多相关DHU内容请搜索靠谱客的其他文章。
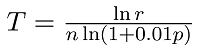
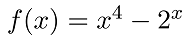








发表评论 取消回复