一、 计算公式

在shannon提出信息论到现在已经有70多年的历史。信息论中常用的概念有信息熵、联合熵、条件熵、互信息等概念。

1、信息熵H(X)

定义：一个离散随机变量X的熵H(X)定义为
$$H(X)=-\sum _{x\in \chi }p(x)\log p(x)$$

2、联合熵H(X,Y)

定义：对于服从联合分布为p(x,y)的一对离散随机变量(X,Y)，其联合熵H(X,Y) (joint entropy)定义为：
$$H(X,Y)=-\sum _{x\in X}\sum _{y\in Y}p(x,y)\log p(x,y)$$

3、互信息I(X,Y)

定义：考虑两个随机变量X和Y，他们的联合概率密度函数为p(x,y)，其边际概率密度函数分别为p(x)和p(y)。互信息I(X;Y)为联合分布p(x,y)和p(x)p(y)之间的相对熵，即：
$$I(X;Y)=\sum _{x\in \chi }\sum _{y\in \nu }p(x,y)\log \frac{p(x,y)}{p(x)p(y)}$$

4、条件熵H(X|Y)

定义：若（X，Y)~p(x,y)，条件熵(Conditional entropy) H(Y|X)定义为：
$$\begin{gathered} H(Y|X)=\sum _{x\in \chi }p(x)H(Y|X=x)=-\sum _{x\in \chi }p(x)\sum _{y\in \nu }p(y|x)\log p(y|x) \\ =-\sum _{x\in \chi }\sum _{y\in \nu }p(x,y)\log (y|x)=-E\log p(Y|X) \end{gathered}$$

二、举例说明

为了对以上公式进行更加直观的理解，通过以下例子对信息熵、联合熵、条件熵、互信息、条件互信息进行举例。

1、信息熵H(X)

假设有两个二进制的变量X和Y
x = [1 0 1 1 0]’;
y = [1 1 1 0 0]’;
根据概率
p(x=0)=2/5; p(x=1)=3/5;
p(y=0)=2/5; p(y=1)=3/5;
$$H(x)=-\frac{2}{5}\ast \log (\frac{2}{5})-\frac{3}{5}\ast \log (\frac{3}{5})=0.9710$$
同理计算得到$h(y)=0.9710$

2、联合熵H(X,Y)

要计算H(X,Y)，需要先知道P(X,Y)。

根据X，Y的值可以得到P(X,Y)：
上图绿色标记：$p(x=0;y=0)=1/5$
上图红色标记：$p(x=0;y=1)=1/5$
上图蓝色标记：$p(x=1;y=0)=1/5$
上图黄色标记：$p(x=1;y=1)=2/5$
得到(X,Y)的分布律如下：

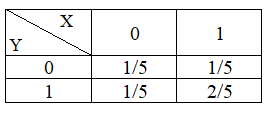
最终计算H(X,Y)得到：
$$\begin{array}{rl}H(X,Y)=& -\frac{1}{5}\ast \log (\frac{1}{5})-\frac{1}{5}\ast \log (\frac{1}{5})\\ & \\ & -\frac{1}{5}\ast \log (\frac{1}{5})-\frac{2}{5}\ast \log (\frac{2}{5})\\ =& 1.9219\end{array}$$

3、互信息I(X,Y)

$$\begin{array}{rl}I(X;Y)=& H(X)+H(Y)-H(X,Y)\\ =& 0.9710+0.9710-1.9219\\ =& 0.02\end{array}$$

4、条件熵H(X|Y)

根据(X,Y)的分布律可知：

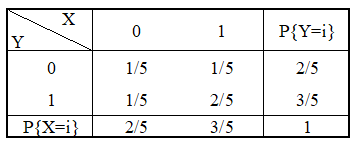
其中$P(X=0|Y=0)$表示在Y=0的情况下X=0的概率，可计算得到：
$$\begin{gathered} P(X=0|Y=0)=\frac{P(X=0,Y=0)}{P(Y=0)}=\frac{1/5}{2/5}=1/2 \\ P(X=1|Y=0)=\frac{P(X=1,Y=0)}{P(Y=0)}=\frac{1/5}{2/5}=1/2 \\ P(X=0|Y=1)=\frac{P(X=0,Y=1)}{P(Y=1)}=\frac{1/5}{3/5}=1/3 \\ P(X=1|Y=1)=\frac{P(X=1,Y=1)}{P(Y=1)}=\frac{2/5}{3/5}=2/3 \end{gathered}$$
通过以上计算可到条件互信息为：
$$\begin{array}{rl}H(X|Y)=& -\sum _{Y}P(Y)\log P(X|Y)\\ =& -P(Y=0)[H(P(X=0|Y=0)+H(P(X=1|Y=0)]\\ & -P(Y=1)[H(P(X=0|Y=1)+H(P(X=1|Y=1))]\\ =& -(2/5)\ast [(1/2)\ast \log (1/2)+(1/2)\ast \log (1/2)]\\ & -(3/5)\ast [(1/3)\ast \log (1/3)-(2/3)\ast \log (2/3)]\\ =& 0.9510\end{array}$$

也可以通过公式
$$\begin{array}{rl}H(X|Y)=& H(X)-I(X;Y)\\ =& 0.9710-0.02\\ =& 0.9510\end{array}$$

总结

通过举例X，Y对信息熵、联合熵、条件熵和互信息进行计算，加深对信息熵等概念的理解。

最后

以上就是明亮纸鹤为你收集整理的举例说明信息熵、互信息的计算过程一、 计算公式二、举例说明总结的全部内容，希望文章能够帮你解决举例说明信息熵、互信息的计算过程一、 计算公式二、举例说明总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。