信息熵、条件熵、信息增益率

1.1 数学分布

分布可能指代不同的东西，比如数据分布或概率分布。这两种分布其实没有本质的区别，可以将x看做随机点，某一数据分布P为目标分布，概率分布f为x落在P上的概率值，形式化表示为f(x)。

假设我们是一组正在广袤无垠的太空中进行研究的科学家。我们发现了一些太空蠕虫，这些太空蠕虫的牙齿数量各不相同。现在我们需要将这些信息发回地球。但从太空向地球发送信息的成本很高，所以我们需要用尽量少的数据表达这些信息。我们有个好方法：我们不发送单个数值，而是绘制一张图表，其中 X 轴表示所观察到的不同牙齿数量（0,1,2…），Y 轴是看到的太空蠕虫具有 x 颗牙齿的概率（即具有 x 颗牙齿的蠕虫数量/蠕虫总数量）。这样，我们就将观察结果转换成了分布。

1.2 信息熵

熵是信息混乱程度的度量，信息越混乱越不确定熵越小。

我们对于信息发生概率的度量依赖于概率分布p(x)，而我们想要寻找一个函数h(x)，它是概率p(x)的单调函数，表达了信息内容的多少。信息量函数h()的形式可以这样寻找：如果我们有两个不相关的事件x和y，那么我们观察到两个事件同时发生时获得的信息应该等于观察到事件各自发生时获得的信息之和，即h(x, y)=h(x)+h(y)。两个不相关事件是统计独立的，因此p(x, y)=p(x)*p(y)。根据这两个关系，很容易看出h(x)一定与p(x) 的对数有关。因此，我们有：

其中负号使信息量取值为非负，一个事件发生的概率越大则信息量越小，而本来发生概率很小的事件发生了，那么信息量就很大，比如地震。该公式定义了概率分布和信息量函数成反比的关系。信息量是衡量事件发生时所带有的信息内容的多少。

信息熵是考虑该随机变量的所有可能取值，即所有可能发生事件所带来的信息量的期望。

现在假设一个发送者想传输一个随机变量的值给接收者。这个过程中，他们传输的平均信息量通可以通过计算概率分布p(x) 的期望得到。这个期望值为：

事实上H(x)就是随机变量x的熵，熵计算公式：

信息熵是随机变量所有取值的信息量的期望，即当获取了一个事件的概率分布后，它的信息熵就是确定的，反映了它的平均信息量大小，信息熵越大，平均信息量越大，概率分布越平均（反之，某些取值的概率越大或越小），信息混乱程度越低。

y1 = tf.constant([0.25, 0.25, 0.25, 0.25])
y2 = tf.constant([0.1, 0.1, 0.1, 0.7])
y3 = tf.constant([0.01, 0.01, 0.01, 0.97])
loss1 = -tf.reduce_sum(y1*tf.math.log(y1))
# 1.3862944
loss2 = -tf.reduce_sum(y2*tf.math.log(y2))
# 0.94044805
loss3 = -tf.reduce_sum(y3 * tf.math.log(y3))
# 0.1677005

1.3 条件熵

条件熵H(Y∣X)定义为X给定条件下Y的条件概率的熵对X的数学期望：

条件概率P(y|x)为已知x的情况下y的概率，p(y|x)=p(x, y)-p(x)。

某个事件的条件熵指在另一事件发生的情况下，该事件的熵的期望，例题讲解：

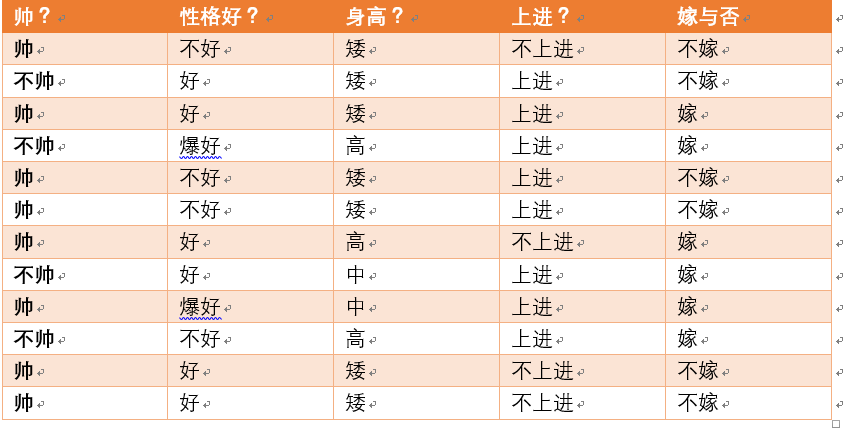
女孩嫁还是不嫁永远是问题中的问题，老感兴趣了，今天就分析一下，那个因素影响巨大。女生嫁不嫁是事件Y，男生帅不帅是事件X，我们想知道的是，帅不帅对女生的决定影响有多大，调查问卷结果见下图，我们可以用条件熵来计算一下，一切用数据说话！

可以看到在调查对象中帅的小伙子有8个，不帅的才4个，在帅哥中，选择嫁的女生有3个，不嫁的有5个，同理，在丑男里，愿意嫁的居然有3个，不愿意的就1个。所以：

故在帅不帅的情况下，嫁不嫁的条件熵为：

观察只有嫁不嫁的信息熵为：

我们用另一个变量对原变量分类后，原变量的熵减小了，信息量减小了，不确定性就会减小了，因为新增了X的信息。可以感受一下，不确定程度减少了多少就是信息的增益。这里可能会有点疑惑，信息量减小了，怎么还叫信息增益呢？其实按常识来说，我们是希望信息越多越好，但信息越多也就意味着选择空间大，不确定性越大，生活嘛，还是稳定最好，至于增益还是衰减，别纠结了，这看人。

1.4 信息增益率

上述的嫁不嫁问题其实还没解决，回顾一下问题：我们想知道的是，帅不帅对女生的决定影响有多大？信息熵回答了我们女生做决定的神奇思路（H越大表示脑回路清奇，可能自己都不知道自己要啥，H越小表示直女癌），而条件熵回答了在帅不帅以经定的情况下，做决定的神奇思路，但还是不知道帅不帅的影响有多大。感觉答案已经呼之欲出了，别急，就是信息增益率。

信息增益指得知特征X的信息而使得类Y的信息不确定性减少的程度。这不就是我们想要的答案吗？计算公式给出：

g(X)为特征X对分类Y的信息增益。

所以男生帅不帅对女生嫁不嫁的信息增益为：

不过，好像只是一个数字也看不出啥，没事还有信息增益率：

同理我们计算一下其他因素的信息增益和信息增益率

如此看来，还是个子高点好啊！但注意，信息增益率之和不是1，因为信息增益是特征对分类的不确定性贡献，而信息增益率的分母是特征本身的不确定性程度，按正常认知来说信息增益率之和也不该是1。所以另一个问题是，信息增益率是1，还是大于1，可能是负数？

最后

以上就是文静嚓茶为你收集整理的信息熵、条件熵、信息增益率的全部内容，希望文章能够帮你解决信息熵、条件熵、信息增益率所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。