一、模型引入

下面有这样一些分类任务：

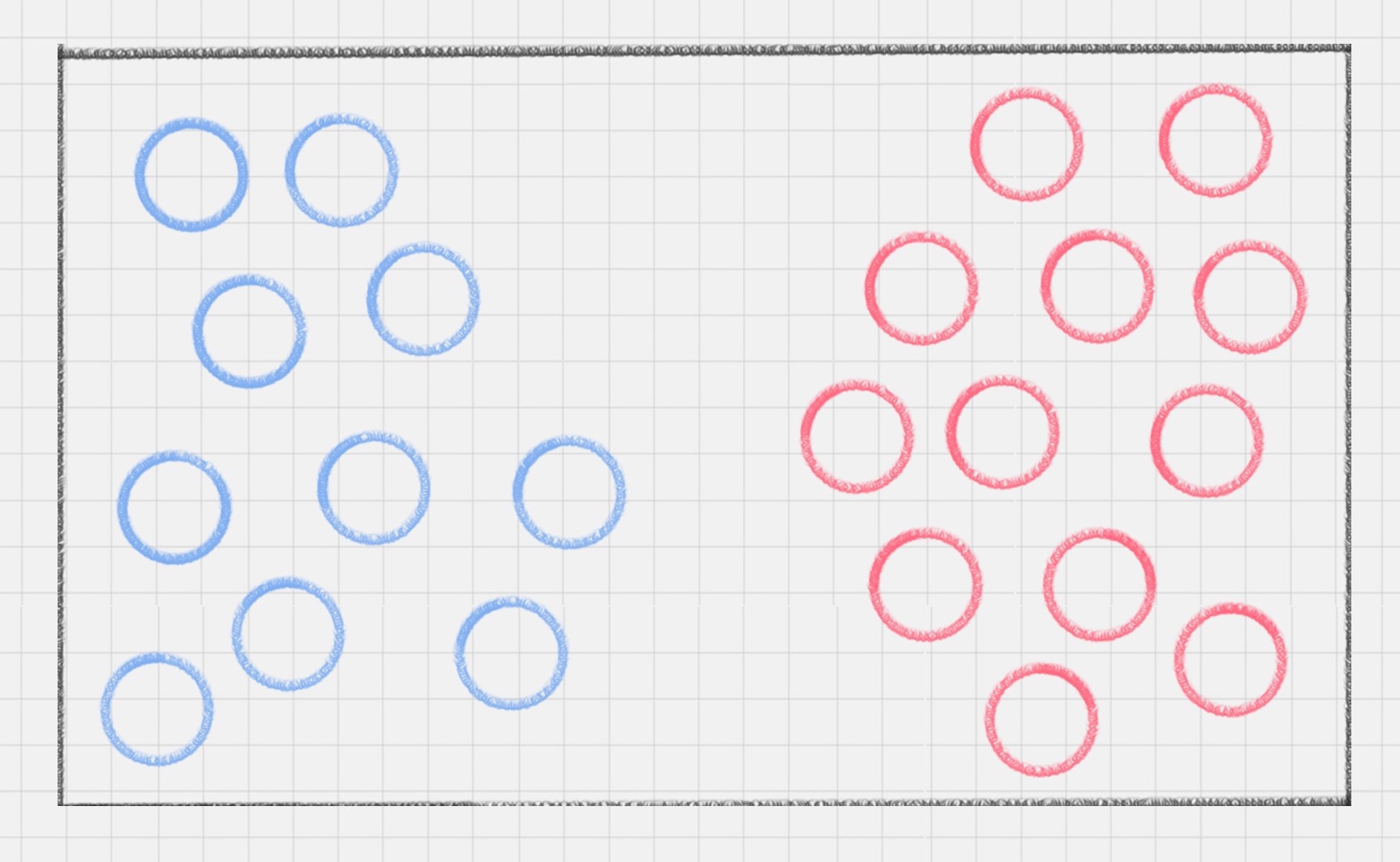
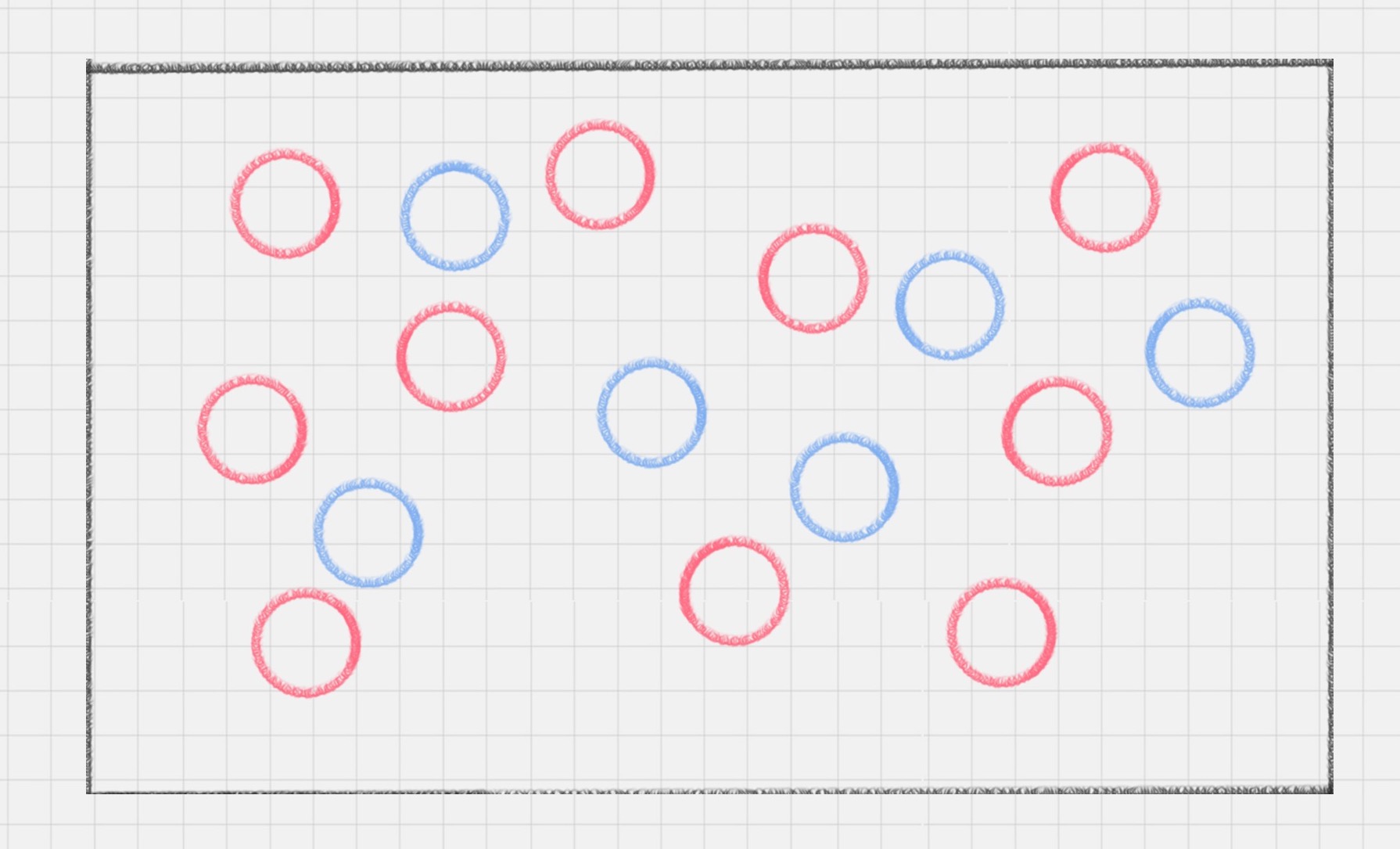
                                        图1                                                                                   图2

        左边很容易分，在中间画一条线即可，但是右边呢？这时有人提出一种思路：把这些点放入更高维度，从数学的角度来看，空间维度越高，点在空间中的分布就越稀疏，也就越线性可分，这样就可以用一个切面(可能是任意维的)把这些点切分。数学上可证明存在n，当这些点如果扩张到n维，一定有且仅有一个n-1维的平面可把它们切分开，这个平面就是超平面。

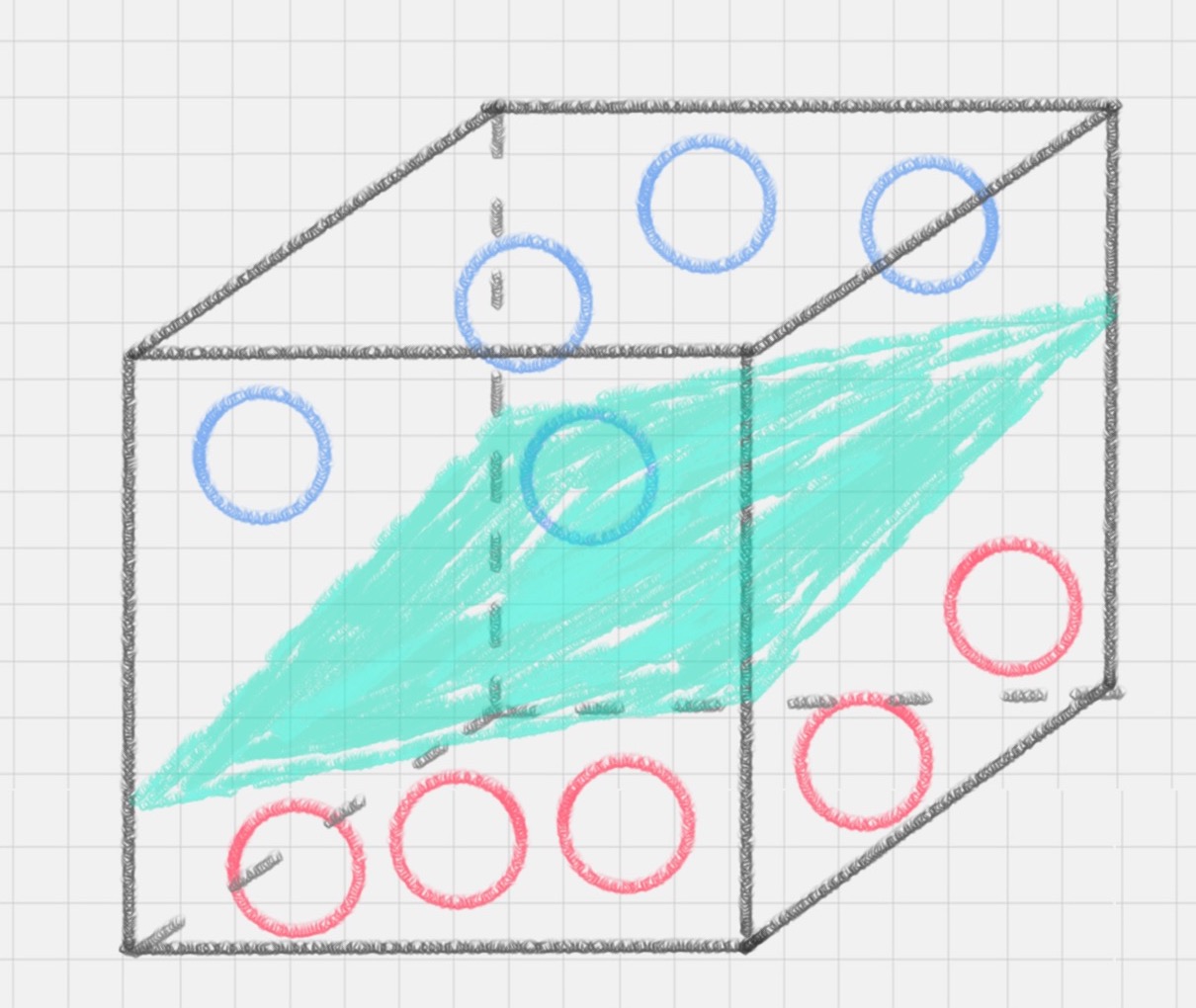
        图3为一个具体例子，把图2放到图3所示的三维空间中，可看出有一个二维平面可把它们切分开，该平面为超平面。

二、工作原理

     1、SVM的定义

        用 SVM 计算的过程就是帮我们找到那个超平面的过程，这个超平面就是我们的 SVM 分类器。

        SVM是常见的一种分类方法,是有监督的学习模型。何为有监督？指的是数据事先就带有标签，比如数据x1,x2,x3都为第k类，又比如在图3中明确知道了哪些小球是蓝色类，哪些是红色类。这样有监督训练之后，SVM可以帮我们进行模式识别、分类以及回归分析。

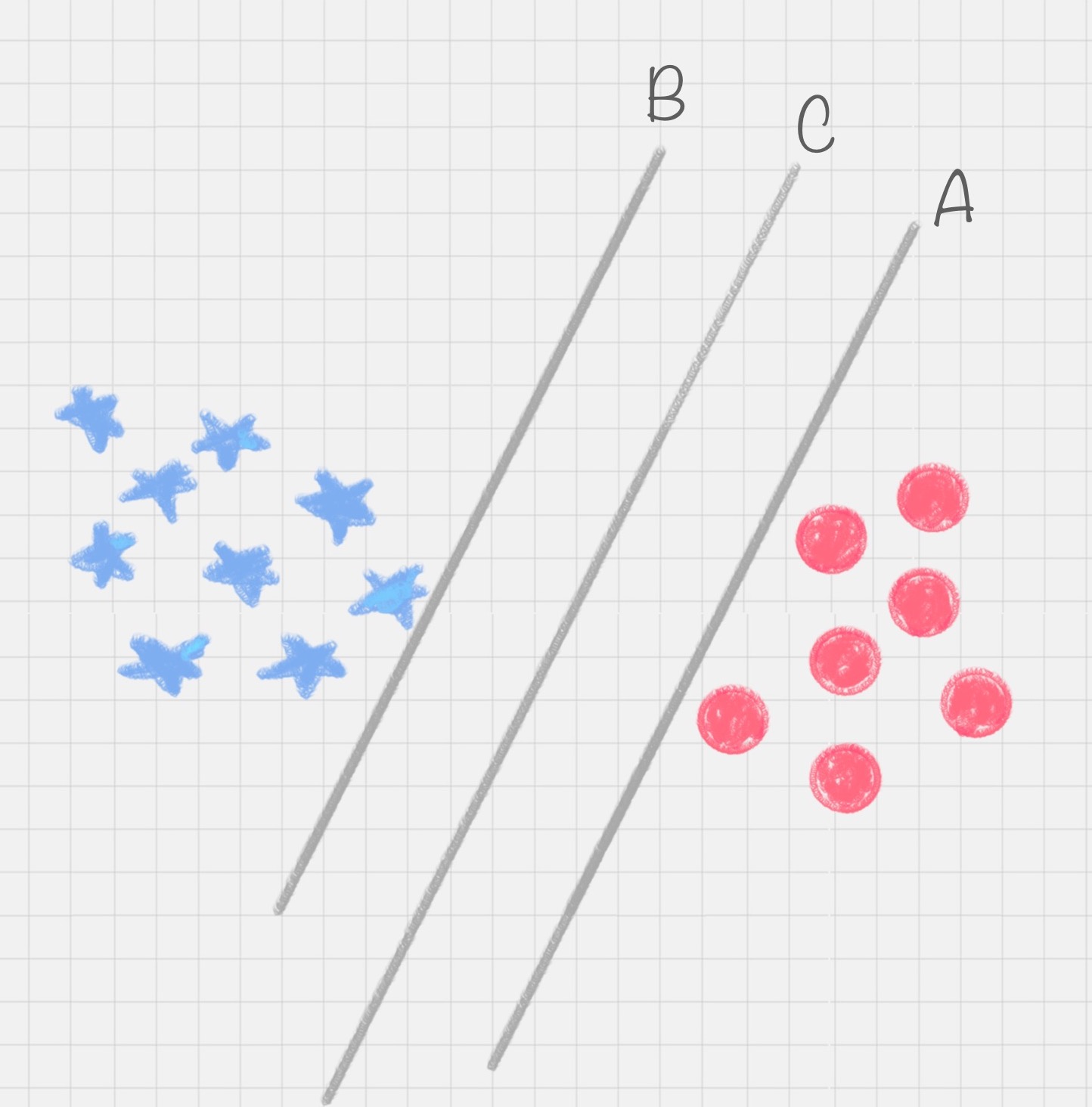
        由图4可以看出来，直线A和C之间有无数条曲线能线性切分红蓝数据点，但其中最优的只有一个，直线C。因为直线C位于A和B的中间，能最大限度地避免误差，即鲁棒性更强。因此寻找切分平面C就是SVM的目标。

        为了寻找切分平面C，需要定义几个概念：

      （1）超平面的表达式：

      （2）分类间隔：A，B分别到C的距离

      （3）硬间隔：假如数据是完全的线性可分的，那么学习到的模型可以称为硬间隔支持向量机

      （4）软间隔：由于数据噪声，允许一定量的样本分类错误，则称为软间隔支持向量机

        SVM的目标：帮我们找到一个超平面，这个超平面能将不同的样本划分开，同时使得样本集中的点到这个分类超平面的最小距离（即分类间隔）最大化。

     2、多分类SVM

       原本SVM只是一个二分类器，现在要拓展到多分类可以用两种方法，“一对多法”和“一对一法”。

•   一对多法

        假设我们要把物体分成 A、B、C、D 四种分类，那么我们可以先把其中的一类作为分类 1，其他类统一归为分类 2。这样我们可以构造 4 种 SVM，分别为以下的情况：

      （1）样本 A 作为正集，B，C，D 作为负集；

      （2）样本 B 作为正集，A，C，D 作为负集；

      （3）样本 C 作为正集，A，B，D 作为负集；

      （4）样本 D 作为正集，A，B，C 作为负集。

        这种方法，针对 K 个分类，需要训练 K 个分类器，分类速度较快，但训练速度较慢，因为每个分类器都需要对全部样本进行训练，而且负样本数量远大于正样本数量，会造成样本不对称的情况，而且当增加新的分类，比如第 K+1 类时，需要重新对分类器进行构造。

•   一对一法

        一对一法的初衷是想在训练的时候更加灵活。我们可以在任意两类样本之间构造一个 SVM，这样针对 K 类的样本，就会有 C(k,2) 类分类器。比如我们想要划分 A、B、C 三个类，可以构造 3 个分类器：

     （1）分类器 1：A、B；

     （2）分类器 2：A、C；

     （3）分类器 3：B、C。

       当对一个未知样本进行分类时，每一个分类器都会有一个分类结果，即为 1 票，最终得票最多的类别就是整个未知样本的类别。

       优点：如果新增一类，不需要重新训练所有的 SVM，只需要训练和新增这一类样本的分类器。而且这种方式在训练单个 SVM 模型的时候，训练速度快。

       缺点：分类器的个数与 K 的平方成正比，所以当 K 较大时，训练和测试的时间会比较慢。

三、参考文献

1、周志华《机器学习》

2、陈旸《数据分析实战45讲》

最后

以上就是羞涩乐曲为你收集整理的数据分析算法学习（1）：SVM一、模型引入 二、工作原理三、参考文献的全部内容，希望文章能够帮你解决数据分析算法学习（1）：SVM一、模型引入 二、工作原理三、参考文献所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。