1. 系统的极点和零点
传递函数为确定重要的系统响应特性提供了不需要求解完整的微分方程的理论。
复数 s = ρ + jω
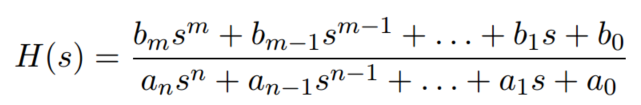
可以写成
z1 z2...zm 为零点 H(s) -> 0
p1 p2 ...pn为极点 H(s) - > ∞
example1:
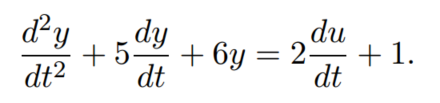
传递函数为
2 s + 1
H(s) = -------------
s^2 + 5 s + 6
1 s + 1/2
H(s) = --- ---------------------
2 (s-（-3))(s-(-2))
零点 s = -1/2
极点 s = -3 和 s = -2
example2:
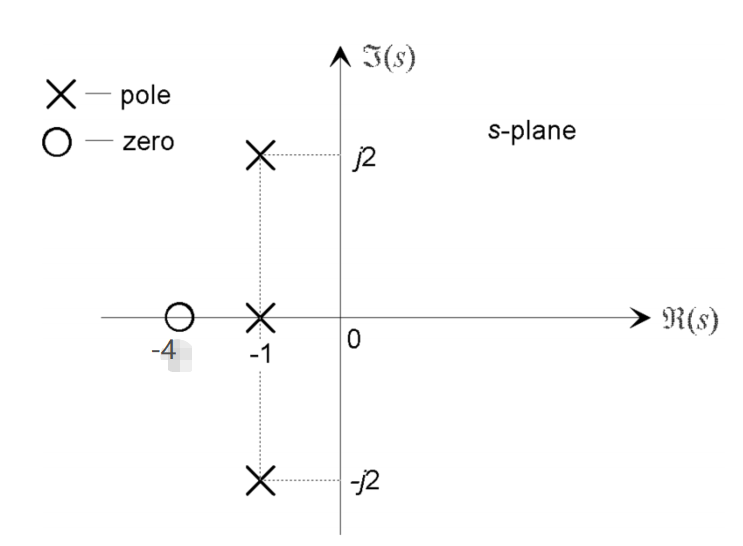
一个系统，极点为 p1 ,p2 = -1±j2 ,一个零点为 z = -4,增益 K = 3, 则 系统响应函数为：
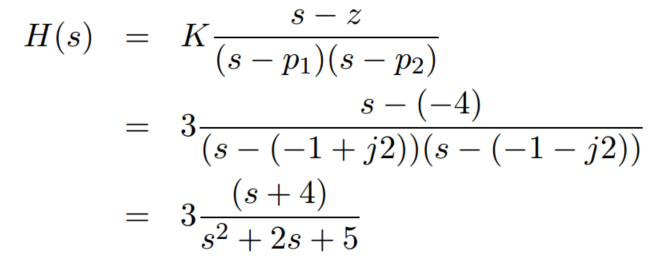
等效的微分方程
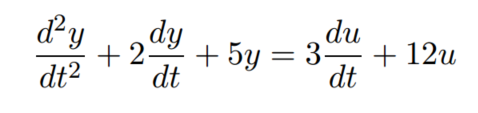
2. 传递函数的几何分析
对于复数函数，可以等效为向量的表示方法
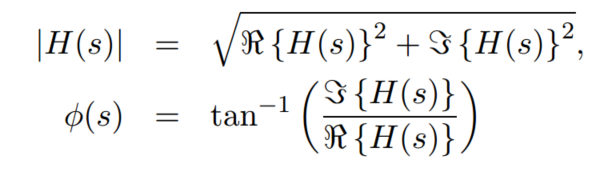
对于
分母的每一项，都可以表示成：
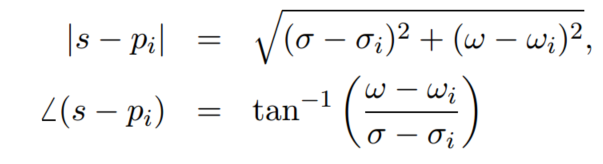
因此
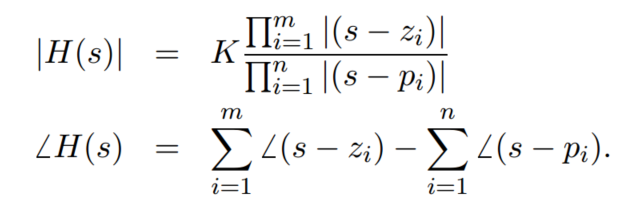
example:
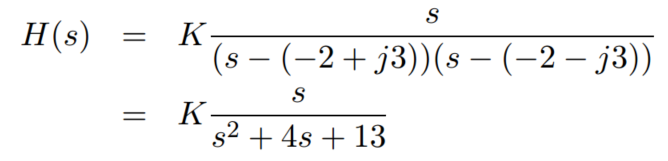
当s = 0 + j5 时
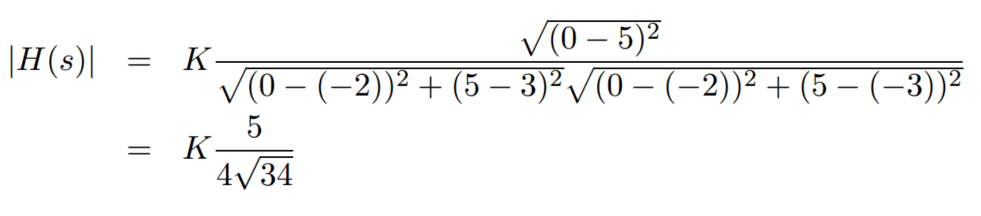
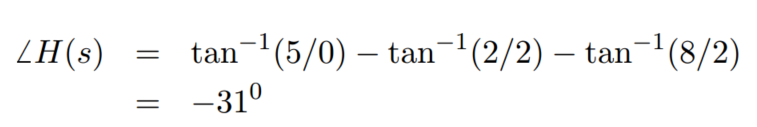
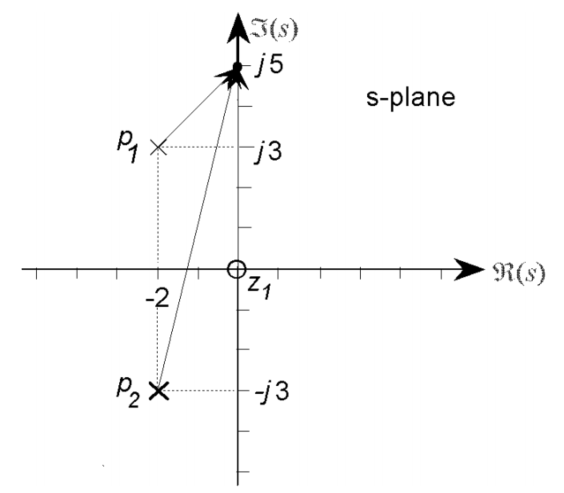
因此 传递函数的响应特性，可以从图上表示出来 对某一个信号的增益，相位的改变，都可以用作图的方法分析，简单又直观。
最后
以上就是哭泣歌曲最近收集整理的关于传递函数极点和零点的几何表示的全部内容，更多相关传递函数极点和零点内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
![自动控制原理MATLAB实验一、求传递函数 二、状态方程描述的系统模型 三、不同模型之间的互换 G1=zpk([],[0,-1,-2],4)%模型一 四、建立复杂的数学模型 五、稳定性分析 六、求解时域响应 七、根轨迹分析](https://file2.kaopuke.com:8081/files_image/reation/bcimg1.png)
发表评论 取消回复