动态系统或动力学系统:运动状态按照确定规律或确定统计规律随时间演化的一类系统,可以分为连续变量动态系统和离散事件动态系统。
连续变量动态系统服从于物理学定律(电力学、力学、热学的定律等)或广义物理学定律(经济学定律、人口学定律、生态学定律、社会学定律),其数学模型可以表示为传统意义下的微分方程或差分方程。
描述连续时间系统的数学模型一般为微分方程
描述离散时间系统的数学模型一般是差分方程
线性系统可以分为线性时不变(定常)系统和线性时变系统,在线性时变系统中,只要参数随时间的变化远慢于系统状态随时间的变化,那么就可以近似为一个线性时不变系统。
外部描述:只是对系统的一种不完全描述,不能反应黑箱内部结构的不能控或不能观测的部分
内部描述:是系统的一种完全的描述,能够完全表征系统结构的一切部分,能够完全反应系统的所有动力学特征
内部描述是基于系统的内部结构分析的一类数学模型,由两个方程来表征:
状态方程:反应系统状态变量组和输入变量组之间的动态关系,其数学表达式对于连续时间系统为一阶微分方程,对于离散时间系统为一阶差分方程
因为输入引起状态变化是一个动态过程
输出方程:反应系统状态变量组与输入变量组和输出变量组之间的转换关系,数学表达式为代数方程组
状态与输入导致输出变化是一个转换过程
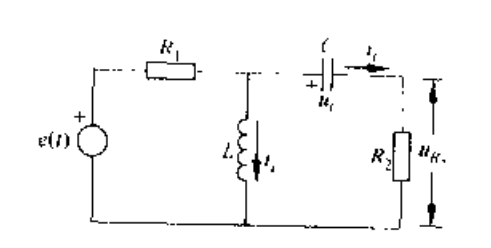
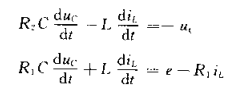
用矩阵的逆:
机电系统遵循的物理定律包括力学定律、电路定律和电磁定律
连续时间线性定常系统的状态空间描述:
注意每个矩阵的维度
连续时间线性时变系统的状态空间描述:
离散时间线性定常系统的状态空间描述:
离散时间线性时变系统的状态空间描述:
状态空间描述只反映离散时刻上变量组之间的因果关系和转换关系
A-系统矩阵
B-输入矩阵
C-输出矩阵
D-传输矩阵
SI:单输入
MI:多输入
SO:单输出
MO:多输出
LTI:线性时不变系统-线性定常系统
LTV:线性时变系统
脉冲响应适用于LTI和LTV,而传递函数仅适用于LTI系统
连续时间状态空间模型:
sys_ss=ss(A,B,C,D,...
'InputName',{'input1','input2',...},...
'OutputName',{'output1','output2',...},...
'AtateName',{'input1','input2',...})
离散时间状态空间模型:
sys_ss=ss(A,B,C,D,Ts) Ts表示采样时间。
串联
sys=series(sys1,sys2)
sys=sys2*sys1---------注意顺序对于多输入多输出系统:
sys=series(sys1,sys2,outputs1,inputs2)用来指明第一个系统的输出和第二个系统的输入,注意它们是相互连接的关系,因此维度要一致。
并联
sys=parallel(sys1,sys2)
sys=sys1+sys2对于MIMO系统:
sys=series(sys1,sys2,inputs1,inputs2,outputs1,outputs2)
反馈
sys=feedback(sys1,sys2)---构成一个负反馈,其中sys2在反馈回路上
sys=feedback(sys1,sys2,+1)----正反馈
线性系统的建立:
非线性系统的局部线性化问题就是在平衡点处用泰勒级数进行展开
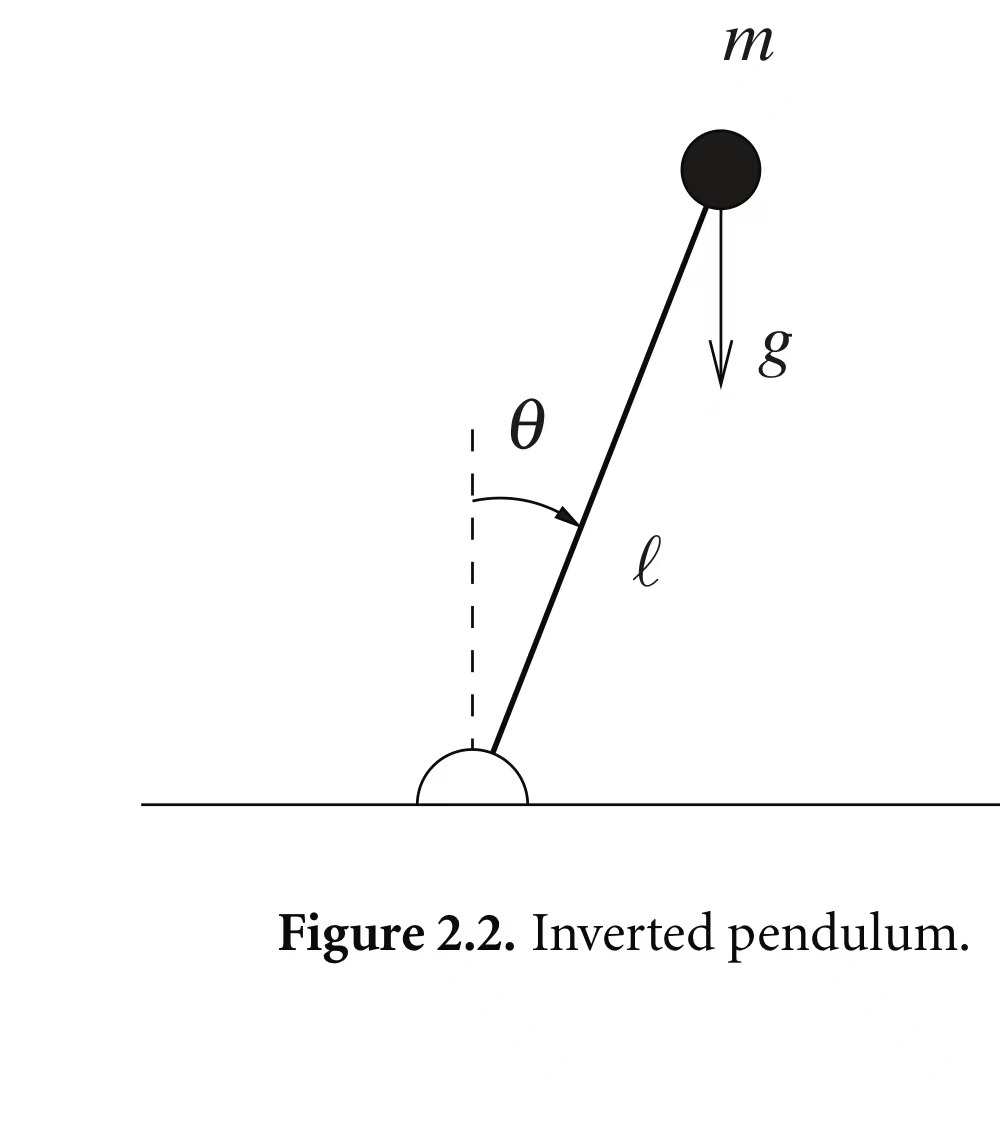
num=[7 2 1]
den=[1 6 11 6]
G=tf(num,den)
p=ss(G)
G =
7 s^2 + 2 s + 1
----------------------
s^3 + 6 s^2 + 11 s + 6
Continuous-time transfer function.
p =
A =
x1 x2 x3
x1 -6 -2.75 -1.5
x2 4 0 0
x3 0 1 0
B =
u1
x1 2
x2 0
x3 0
C =
x1 x2 x3
y1 3.5 0.25 0.125
D =
u1
y1 0
Continuous-time state-space model.
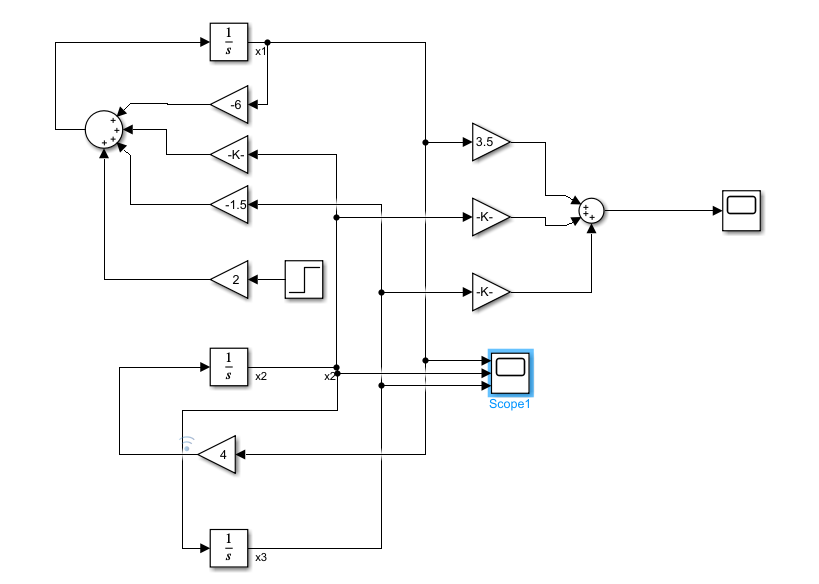
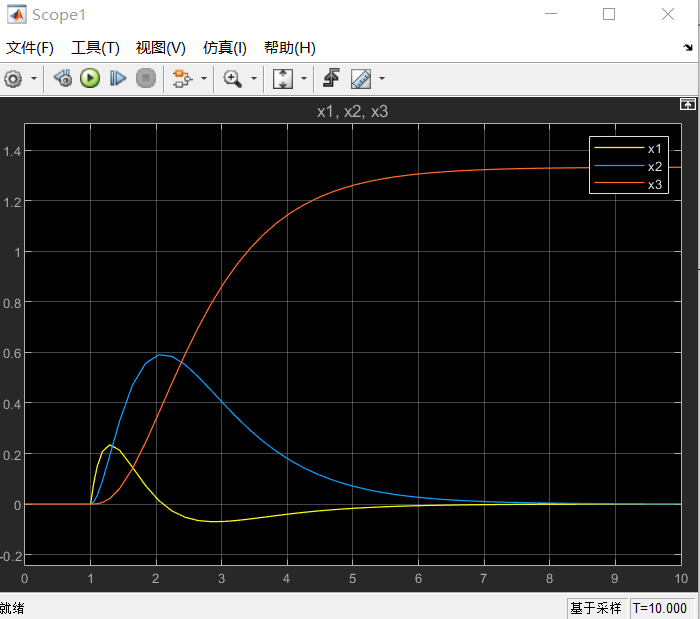
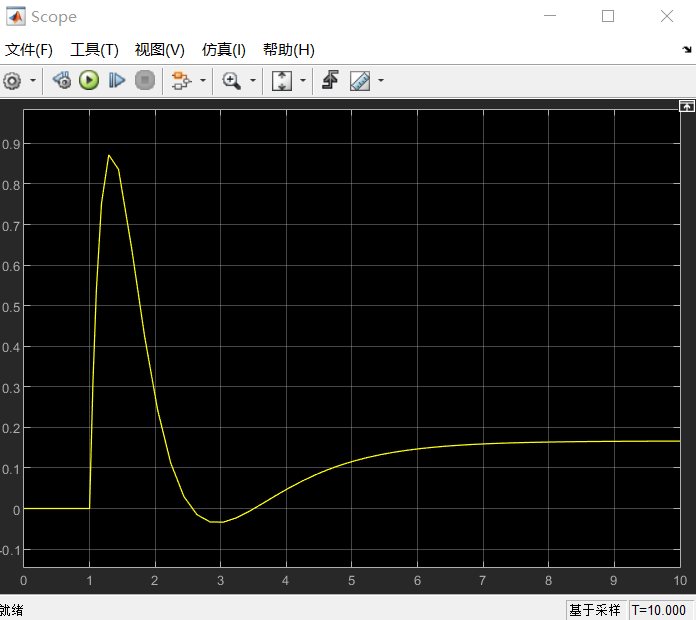
s=tf('s')
G1=(7*s+13)/(s^2+5*+4)
G2=1/(s+2)G=feedback(G1,G2,-1)
G =
7 s^2 + 27 s + 26
-----------------------
s^3 + 2 s^2 + 27 s + 53
Continuous-time transfer function.
G0=ss(G)
G0 =
A =
x1 x2 x3
x1 -2 -6.75 -3.313
x2 4 0 0
x3 0 4 0
B =
u1
x1 4
x2 0
x3 0
C =
x1 x2 x3
y1 1.75 1.688 0.4063
D =
u1
y1 0
Continuous-time state-space model.
特征多项式:
线性时不变系统结构:
从状态方程出发,定义系统的特征矩阵和特征多项式、特征值。
A=[-2 0 1 1;1 -1 1 2;1 2 -1 1;1 1 1 2]
syms s
P=eye(4)
C=s*P-A
det(C)A=[-2 0 1 1;1 -1 1 2;1 2 -1 1;1 1 1 2]
syms s
P=eye(4)
C=s*P-A
det(C)
状态方程的约当规范形:直接以特征值表征系统矩阵的一种状态方程的规范形,
特征值全为单根的情况下意味着系统状态在这种表达下可以实现完全意义下的解耦
其中是以A的特征值为元素的对角矩阵
[V,D] = eig(A)返回特征值的对角矩阵D和矩阵V,其列是对应的右特征向量,使得A*V = V*D
A=[2 -1 -1;0 -1 0;0 2 1]
B=[7;2;3]
[P,D]=eig(A)
A2=inv(P)*A*P
B2=P*B
>> main
A =
2 -1 -1
0 -1 0
0 2 1
B =
7
2
3
P =
1.0000 0.7071 0
0 0 0.7071
0 0.7071 -0.7071
D =
2 0 0
0 1 0
0 0 -1
A2 =
2 0 0
0 1 0
0 0 -1
B2 =
8.4142
2.1213
-0.7071
????????约当规范性有什么用,特别是特征根是重根的情况
当且仅当系统既能控又能观时,系统闭环特征方程式与A的特征多项式一致,并且闭环极点与特征值一致
A=[2 0 0;0 2 0;0 3 1]
B=[1 2;1 0;3 1]
C=[1 1 2]
D=0G=ss(A,B,C,D)
P=tf(G)P =
From input 1 to output:
8 s^2 - 24 s + 16
---------------------
s^3 - 5 s^2 + 8 s - 4
From input 2 to output:
4 s - 6
-------------
s^2 - 3 s + 2G(s)=
最后
以上就是大方画笔最近收集整理的关于第一、二章--绪论、线性系统状态空间描述的全部内容,更多相关第一、二章--绪论、线性系统状态空间描述内容请搜索靠谱客的其他文章。








发表评论 取消回复