matlab状态空间程序,将状态空间表示形式转换为传递函数

理想的一维振荡系统由位于两面墙壁间的两个单位质点 m1 和 m2 组成。每个质点通过一根单位弹性常量弹簧连接到最近的墙壁。另外一根弹簧连接这两个质点。传感器以 Fs=16 Hz 的频率对 a1 和 a2(质点的加速度)采样。

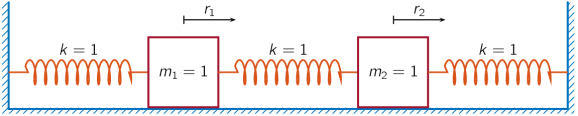
将总测量时间指定为 16 秒。定义采样间隔 Δt=1/Fs。

Fs = 16;

dt = 1/Fs;

N = 257;

t = dt*(0:N-1);

系统可以由状态空间模型描述

x(n+1)=Ax(n)+Bu(n),y(n)=Cx(n)+Du(n),

其中 x=(r1v1r2v2)T 是状态向量，ri 和 vi 分别是第 i 个质点的位置和速度。输入向量 u=(u1u2)T，输出向量 y=(a1a2)T。状态空间矩阵为

A=exp(AcΔt),B=Ac-1(A-I)Bc,C=(-201010-20),D=I,

连续时间状态空间矩阵为

Ac=(0100-2010000110-20),Bc=(00100001),

I 表示合适大小的单位矩阵。

Ac = [0 1 0 0;-2 0 1 0;0 0 0 1;1 0 -2 0];

A = expm(Ac*dt);

Bc = [0 0;1 0;0 0;0 1];

B = Ac(A-eye(4))*Bc;

C = [-2 0 1 0;1 0 -2 0];

D = eye(2);

第一个质点 m1 接收正向的单位脉冲。

ux = [1 zeros(1,N-1)];

u0 = zeros(1,N);

u = [ux;u0];

使用该模型计算系统从全零的初始状态开始的时间演进。

x = [0;0;0;0];

for k = 1:N

y(:,k) = C*x + D*u(:,k);

x = A*x + B*u(:,k);

end

以时间函数形式绘制两个质点的加速度。

stem(t,y','.')

xlabel('t')

legend('a_1','a_2')

title('Mass 1 Excited')

grid

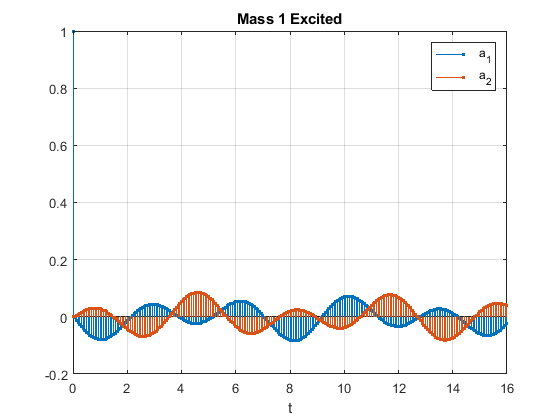
将系统转换为其传递函数表示形式。求得对第一个质点的正单位脉冲刺激的系统响应。

[b1,a1] = ss2tf(A,B,C,D,1);

y1u1 = filter(b1(1,:),a1,ux);

y1u2 = filter(b1(2,:),a1,ux);

绘制结果。传递函数提供与状态空间模型相同的响应。

stem(t,[y1u1;y1u2]','.')

xlabel('t')

legend('a_1','a_2')

title('Mass 1 Excited')

grid

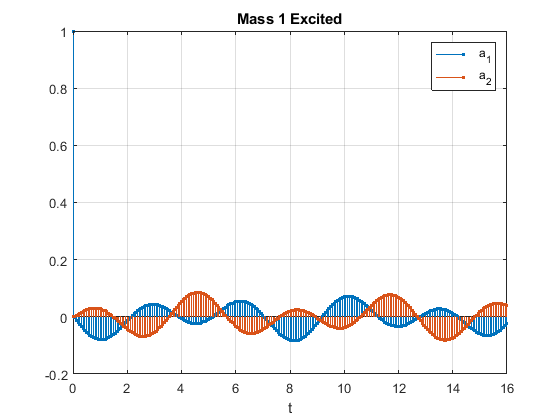
系统将重置为其初始配置。现在，其他质点 m2 接收正向单位脉冲。计算该系统的时间演进。

u = [u0;ux];

x = [0;0;0;0];

for k = 1:N

y(:,k) = C*x + D*u(:,k);

x = A*x + B*u(:,k);

end

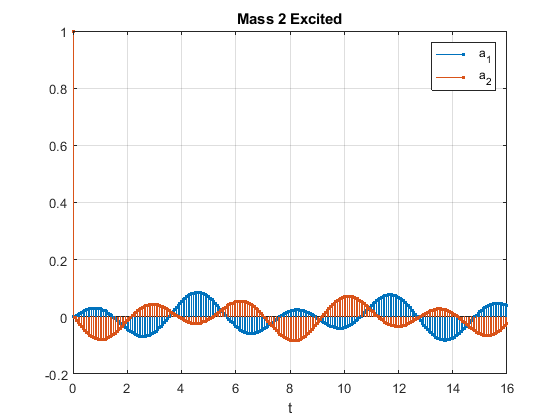
绘制加速度。将交换各个质点的响应。

stem(t,y','.')

xlabel('t')

legend('a_1','a_2')

title('Mass 2 Excited')

grid

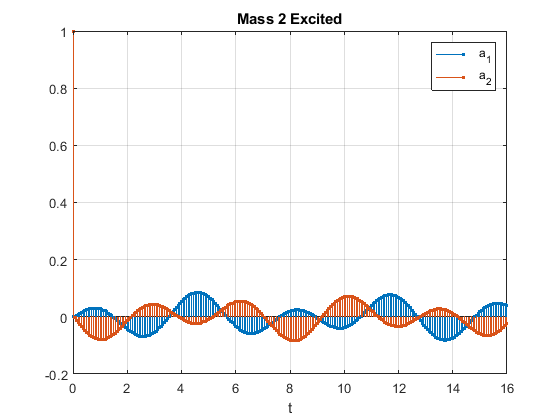
求得对第二个质点的正单位脉冲刺激的系统响应。

[b2,a2] = ss2tf(A,B,C,D,2);

y2u1 = filter(b2(1,:),a2,ux);

y2u2 = filter(b2(2,:),a2,ux);

绘制结果。传递函数提供与状态空间模型相同的响应。

stem(t,[y2u1;y2u2]','.')

xlabel('t')

legend('a_1','a_2')

title('Mass 2 Excited')

grid