目录
一、基础知识
1.传递函数
2.状态方程
二、方法论
1.级联法
2.串联法
3.并联法
三、画系统框图,求状态方程
1.传递函数
2.级联法画系统框图,求状态方程
3.串联法画系统框图,求状态方程
4.并联法画系统框图,求状态方程
一、基础知识
1.传递函数
传递函数是指零初始条件下线性系统响应(即输出)量的拉普拉斯变换(或z变换)与激励(即输入)量的拉普拉斯变换之比。记作G(s)=Y(s) / U(s),其中Y(s)、U(s)分别为输出量和输入量的拉普拉斯变换。
2.状态方程
I/O方程——状态方程。状态方程式刻画系统输入和状态关系的表达式。
如连续线性时变控制系统:
二、方法论
1.级联法
(1) 将传递函数G(s)化为信号流程图
(2) 写状态变量图
(3) 写状态方程和输出方程
2.串联法
串联法从G(s)求状态方程
3.并联法
三、画系统框图,求状态方程
1.传递函数
示例所用传递函数如下:
2.级联法画系统框图,求状态方程
传递函数:
传函方框图:
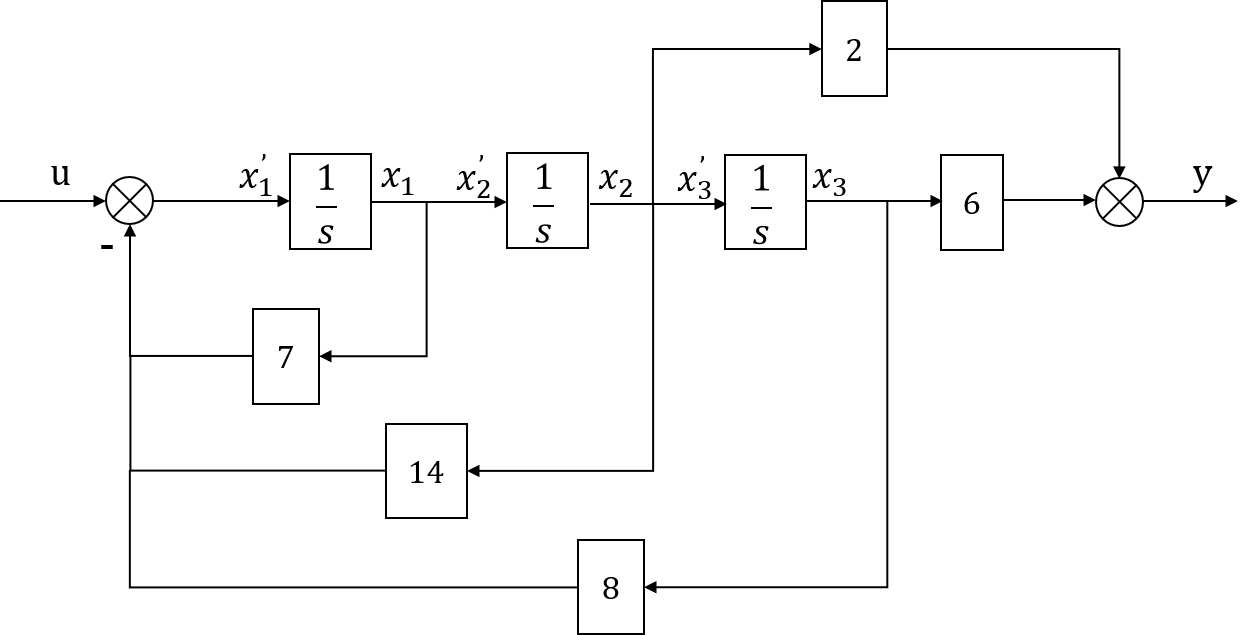
状态方程:
3.串联法画系统框图,求状态方程
传递函数:
传函方框图:

状态方程:
4.并联法画系统框图,求状态方程
传递函数:
传函方框图:
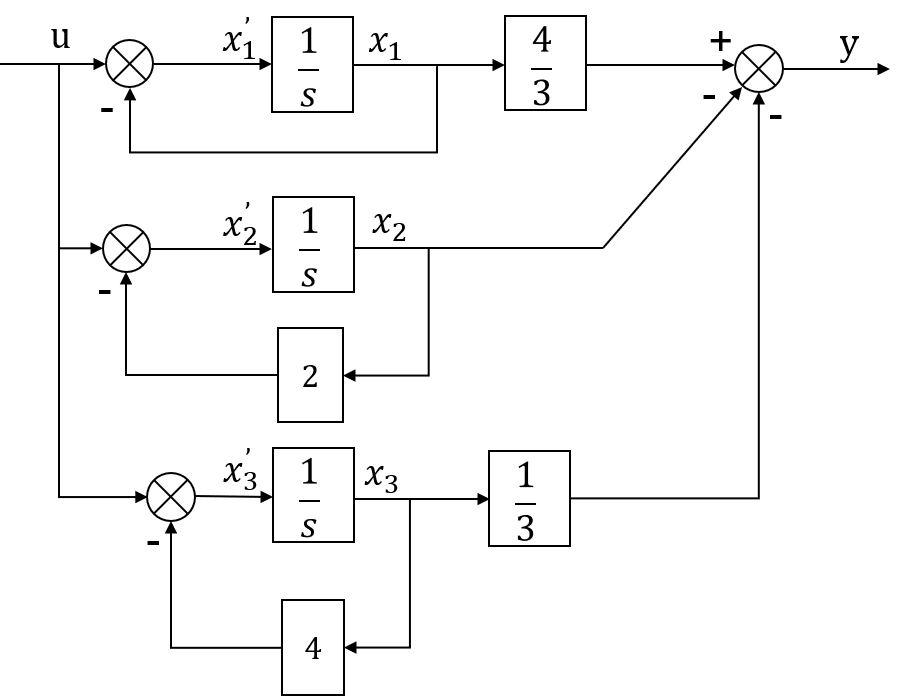
状态方程:
本篇内容就是这些,下一章用仿真程序计算传递函数的结果……
最后
以上就是单身衬衫最近收集整理的关于级联、串联、并联求传递函数的方框图和状态方程一、基础知识二、方法论三、画系统框图,求状态方程的全部内容,更多相关级联、串联、并联求传递函数内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。



![java webrtc降噪_[转]WebRTC 音视频开发总结(十六)](https://www.shuijiaxian.com/files_image/reation/bcimg9.png)




发表评论 取消回复