一阶系统开环传递函数表达式_信号传输笔记(01)—低通系统和带通系统的系统理论...

这里是一则小广告：

关注作者请点击这里哦：zdr0

我的专栏里面不仅有学习笔记，也有一些科普文章，相信我的专栏不会让您失望哦～大家可以关注一下：数学及自然科学

记得点赞加收藏哦～

创作不易，请赞赏一下支持一下作者吧[期待]～

文章中如果有错误的话还请各位大佬多多斧正，感谢！

-尽力写最好的讲义，尽力写最好的科普

推一下我的微信公众号，扫码即可关注哦！今后在知乎所发的文章都会同步到该公众号当中：

http://weixin.qq.com/r/Ky3E3P3Ev6DArbm-93g5 (二维码自动识别)

---

• 无失真系统
• 低通系统
  —理想低通
  —具有非理想传递函数的低通系统
• 带通系统与带通信号
  —理想带通
  —带通系统和等价低通系统
  —信号的复数表示
  —使用带通系统传递带通信号
  —通过低通系统来实现带通系统

说明：本次笔记可能难度有点大，是因为这一块笔记比较重要，所以我就先做了。下面还有一次难度较大的笔记，也比较重要，所以也先做了，之后就开始做基础知识的笔记。 另外，想要学好信号传输，Fourier 变换的基础知识要过硬，推荐一篇我写的文章：

zdr0：史上最全的连续时间 Fourier 变换的性质及其证明（共22条），看到赚到！

后期还会写离散(时间) Fourier 变换等文章，敬请期待。

---

1. 无失真系统

一个系统称为无失真的，当输入信号

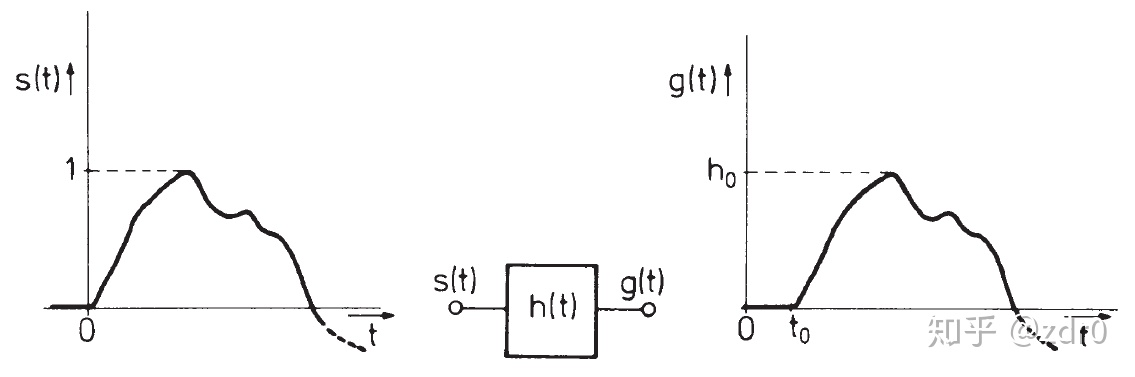
一个无失真系统的传递函数为：

式

可由连续时间 Fourier 变换的

时域位移性质：

推导得出。

该传递函数的模和辐角分别为：

显然，在频域上，无失真系统的传递函数的模为常数，辐角正比于频率

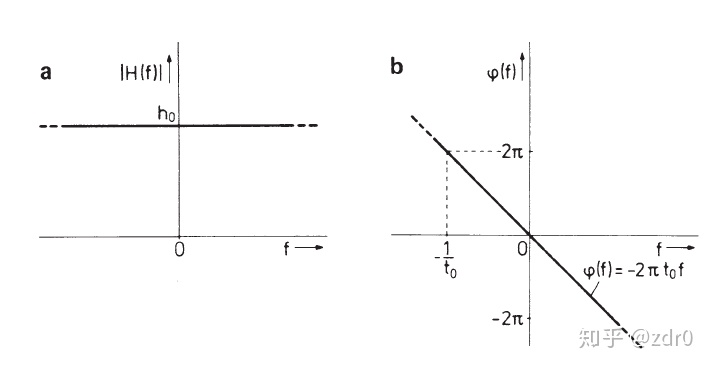
LTI(linear time invariant) 系统的传输特性与无失真系统的理想特性背离，它们无法传输真正形成的信号，因此会产生线性失真。

如果一个系统的传递函数的模

全通系统。

除了使用传递函数的模和相位或实部和虚部之外，还经常使用以下参数来表征一般 LTI 系统的特性：

衰减程度：

衰减角：

：

群时间：

显然，对于一个无失真系统来讲，由于其传递函数的模为常数，所以其衰减程度为一常数。由于相位与频率之间是线性关系，所以其具有一致且不变的相时间和群时间

2. 低通系统

2.1 理想低通

理想低通的传递函数具有这样的特征：其在频率低于截止频率

导通区域。在截止频率纸上就是所谓的 截止区，在该区域上，传递函数为

假设理想系统的时延置

为

矩形函数。

其冲激响应为：

其中：

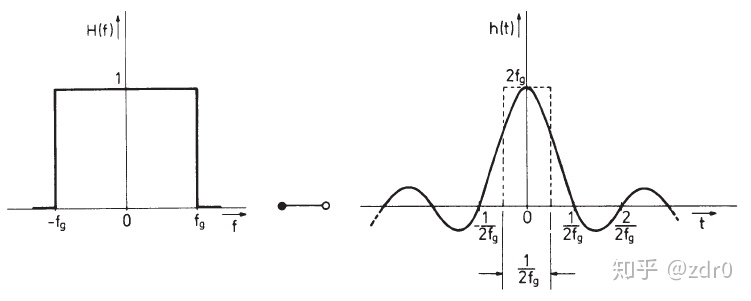
理想低通的冲激响应的波形告诉我们，理想低通不是一个因果系统。

然而，就系统理论而言，正是在这个理想化的低通上，可以清楚地得出时域和频域中的行为之间的几个重要关系，这些关系对于真实的低通系统也是有效的。

与 Dirac 冲激相比，冲激响应

矩形的宽度定义为其信号持续时间

在式

中：

显然，由图片2.1.3可知，对于一个理想低通来讲，其信号持续时间为：

因此，理想的低通滤波器的脉冲响应

这种关系更一般的形式为：

式

时间带宽积，可以根据低通系统以及信号持续时间和带宽的特殊定义而取不同的值。

理想低通的阶跃响应

由冲激响应和阶跃响应之间的关系式：

可以得出理想低通的阶跃响应的表达式为：

现在我们引入所谓的积分正弦函数

该函数具有性质：

和：

式

为

Dirichlet 积分：

上述过程使用了 Laplace 变换的 时域积分性质：

进而由性质

在式

中：

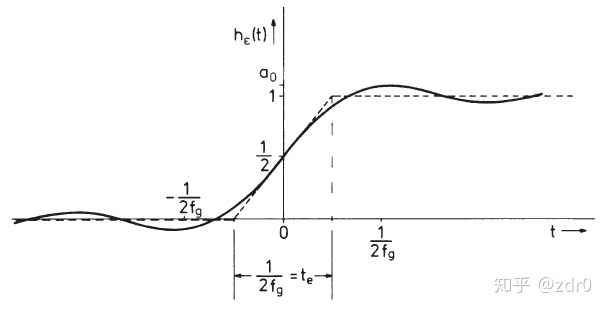
由图片2.2可以看出，理想低通的单位阶跃响应当

稳定时间

且：

则上升时间为：

由式

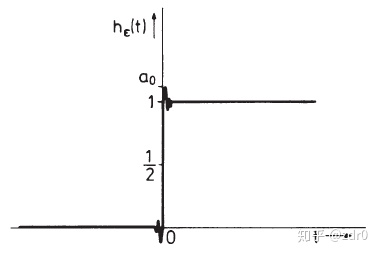
由图片2.3可以看出，截止频率

理想低通的冲激响应

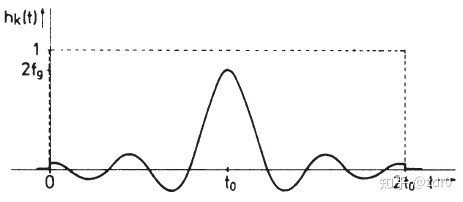
在图片2.4中，将一个理想低通的冲击响应在时域上移动了时间

式

中，利用了关系：

实现了时域上图像的搬移。

从而传递函数

式

中使用了连续时间 Fourier 变换的

时域卷积性质：

和 频域卷积性质：

以及 时域位移性质：

我们可以将矩频域中的形窗函数

进而将式

显然，

2.2 具有非理想传递函数的低通系统

本小节中将要介绍的回声方法(echo methode)可以实现在频域和时域中清楚地表示出近似于矩形的低通传递函数。

根据采样定理，低通系统的每个低通信号以及每个低通系统的冲激响应都可以表示为

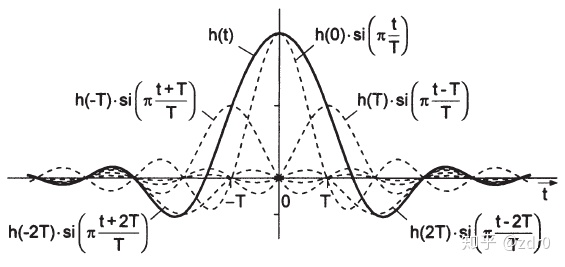
式

一般低通系统的冲激响应。图片2.5给出了五个 回声。其中 回声幅度。

通过对式

对

如要计算回声幅度

特别的，当冲激响应是偶的时候

且：

式

用到的性质是：偶的实函数的 Fourier 变换也是偶和实的。

3. 带通系统与带通信号

3.1 理想带通

理想带通只在带宽

其中

中间频率。我们可以将式

现在我们对式

在式

中：

式

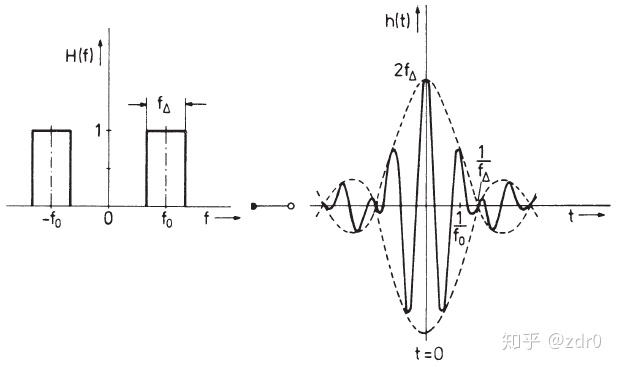
3.2 带通系统与等价低通系统

给定一个任意的带通系统

反对称的函数。

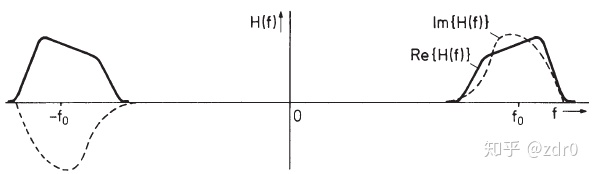
根据理想带通的表示，现在也可以用等效低通的传递函数

载波频率

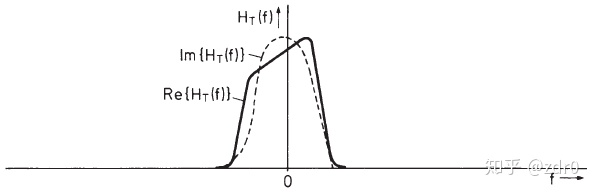
则：

在一般带通系统的这种表示中，式

给定的具有实冲激响应的带通系统可以被分配给任意数量的具有不同传递函数

在某些带通系统中，通带内存在

对称带通系统。

由于冲激响应是实的，所以根据实函数的 Fourier 变换的性质：

一个十分典型的带通系统的例子就是我们最开始讲的理想带通：我们按照构造

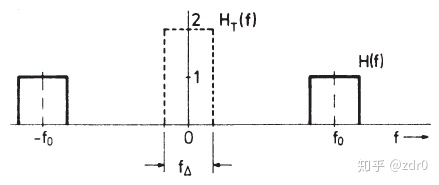
显然， 该等价低通的传递函数是：

冲激响应为：

但是，应该注意的是，这种情况非常特殊，因为即使在对称带通系统中，频谱的虚部也通常存在。

3.3 信号的复数表示

由逆 Fourier 变换的共轭性质：

和频域位移性质：

我们可以得到式

因此，在式

带通信号

其中，

包络线， 复载体。它们乘积的一半被称为带通信号的解析分量

所以：

特别的，对于一个实值信号来讲：

式

与

Hilbert 变换有关，在后面的笔记中会整理到。

我们将式

定义：

所以：

其中，

正交分量。进一步有复包络线的长度：

复包络线

此外，

使用辅助角公式可以将

对于对称带通来讲，它的包络线是实值的，则此时式

3.4 使用带通系统传递带通信号

在一个具有冲激响应的

对式

现在我们通过等价低通系统来计算

然后我们对式

而

如果

则式

也可以写为：

比较式

我们对式

其中

带通系统的等价低通冲激响应。而：

3.5 通过低通系统来实现带通系统

一个具有复包络线

然后我们将式

如果输入信号可以分解成正交分量

为此，将

现在应该假设带通系统的频带限制为：

在该假设下，

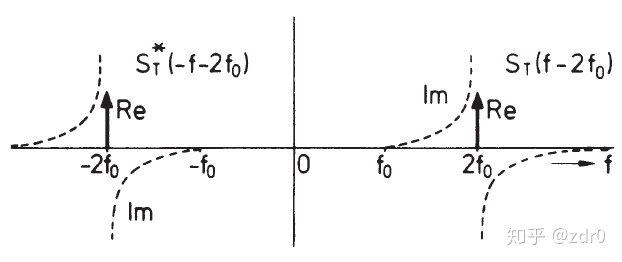
为了生成

由式

使用同样的方式可以生成

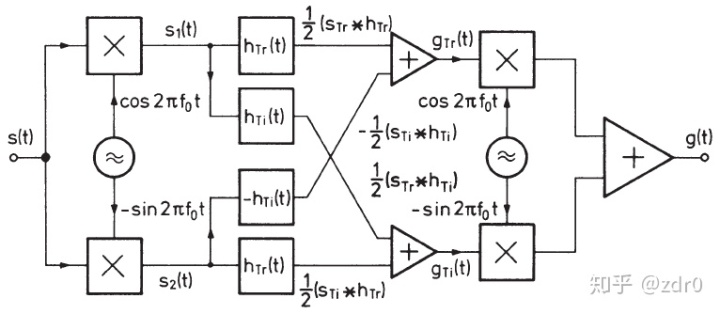
如图片3.5所示的系统，可以使用该系统执行刚才所讨论的操作。其工作工作原理时：首先，将输入信号

---

参考