数字域
freqz 使用基于 FFT 的算法来计算数字滤波器的 Z 变换频率响应。具体来说,语句
[h,w] = freqz(b,a,p)
返回数字滤波器的包含 p 个点的复频率响应 H(ejω)。
H(ejω)=b(1)+b(2)e−jω+...+b(n+1)e−jωna(1)+a(2)e−jω+...+a(m+1)e−jωm
在其最简单的形式中,freqz 接受滤波器系数向量 b 和 a 以及整数 p(该整数指定计算频率响应所用的点的数量)。freqz 以弧度/秒为单位返回向量 h 中的复频率响应,以及向量 w 中的实际频率点。
freqz 可以接受其他参数,例如采样频率或由任意数量的频率点构成的向量。以下示例求 12 阶 Chebyshev I 类滤波器的 256 点频率响应。调用 freqz 将采样频率 fs 指定为 1000 Hz:
[b,a] = cheby1(12,0.5,200/500);
[h,f] = freqz(b,a,256,1000);
由于参数列表包含采样频率,因此 freqz 返回向量 f,其中包含在频率响应计算中使用的 0 到 fs/2 之间的 256 个频率点。
注意
此工具箱使用单位频率是 Nyquist 频率的约定,定义为采样频率的一半。所有基本滤波器设计函数的截止频率参数均用 Nyquist 频率进行归一化处理。例如,对于采样频率为 1000 Hz 的系统,300 Hz 等于 300/500 = 0.6。要将归一化频率转换为围绕单位圆的角频率,请乘以 π。要将归一化频转换回赫兹,请乘以采样频率的一半。
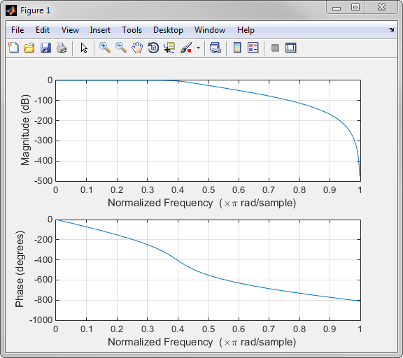
如果您在不带输出参数的情况下调用 freqz,它会同时绘制幅值对频率的图和相位对频率的图。例如,截止频率为 400 Hz、基于 2000 Hz 的采样频率的九阶 Butterworth 低通滤波器是:
[b,a] = butter(9,400/1000);
要计算此滤波器的 256 点复频率响应,并使用 freqz 绘制幅值和相位,请使用
freqz(b,a,256,2000)
freqz 也可以接受由任意数量的频率点构成的向量,以用于频率响应计算。例如,
w = linspace(0,pi);
h = freqz(b,a,w);
计算由向量 b 和 a 定义的滤波器在 w 的频率点处的复频率响应。频率点可以是 0 到 2π 范围内的值。要指定从零到采样频率的频率向量,请在参数列表中同时包括频率向量和采样频率值。
下列示例说明如何计算和显示数字频率响应。传递函数的频率响应
计算并显示由以下传递函数描述的三阶 IIR 低通滤波器的幅值响应:
H(z)=0.05634(1+z-1)(1-1.0166z-1+z-2)(1-0.683z-1)(1-1.4461z-1+0.7957z-2).
将分子和分母表示为多项式卷积。求分布在整个单位圆上的 2001 个点上的频率响应。
b0 = 0.05634;
b1 = [1 1];
b2 = [1 -1.0166 1];
a1 = [1 -0.683];
a2 = [1 -1.4461 0.7957];
b = b0*conv(b1,b2);
a = conv(a1,a2);
[h,w] = freqz(b,a,'whole',2001);
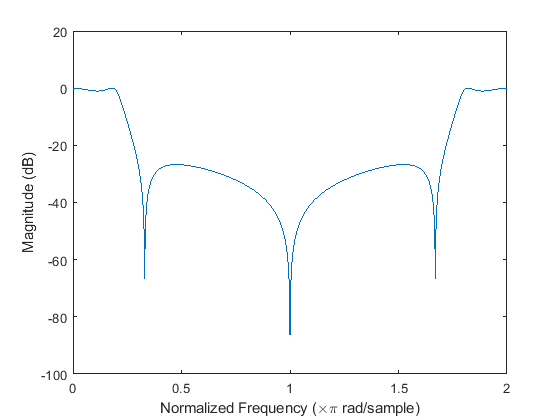
绘制以分贝表示的幅值响应。
plot(w/pi,20*log10(abs(h)))
ax = gca;
ax.YLim = [-100 20];
ax.XTick = 0:.5:2;
xlabel('Normalized Frequency (timespi rad/sample)')
ylabel('Magnitude (dB)')
 FIR 带通滤波器的频率响应
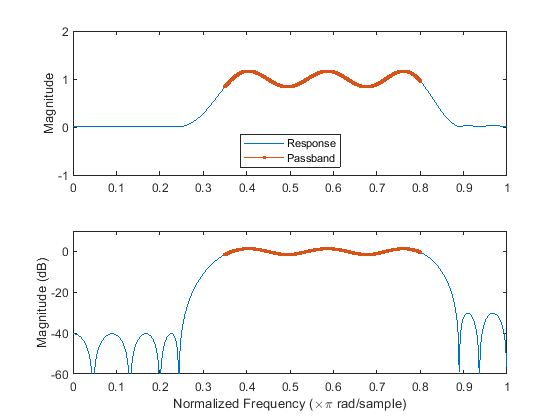
FIR 带通滤波器的频率响应
设计一个 FIR 带通滤波器,通带在 0.35π 和 0.8π 弧度/采样点之间,波纹为 3 dB。第一个阻带是从 0 到 0.1π 弧度/采样点,衰减为 40 dB。第二个阻带是从 0.9π 弧度/采样点到 Nyquist 频率,衰减为 30 dB。计算频率响应。同时以线性单位和分贝绘制其幅值。突出显示通带。
sf1 = 0.1;
pf1 = 0.35;
pf2 = 0.8;
sf2 = 0.9;
pb = linspace(pf1,pf2,1e3)*pi;
bp = designfilt('bandpassfir', ...
'StopbandAttenuation1',40, 'StopbandFrequency1',sf1,...
'PassbandFrequency1',pf1,'PassbandRipple',3,'PassbandFrequency2',pf2, ...
'StopbandFrequency2',sf2,'StopbandAttenuation2',30);
[h,w] = freqz(bp,1024);
hpb = freqz(bp,pb);
subplot(2,1,1)
plot(w/pi,abs(h),pb/pi,abs(hpb),'.-')
axis([0 1 -1 2])
legend('Response','Passband','Location','South')
ylabel('Magnitude')
subplot(2,1,2)
plot(w/pi,db(h),pb/pi,db(hpb),'.-')
axis([0 1 -60 10])
xlabel('Normalized Frequency (timespi rad/sample)')
ylabel('Magnitude (dB)')
 高通滤波器的幅值响应
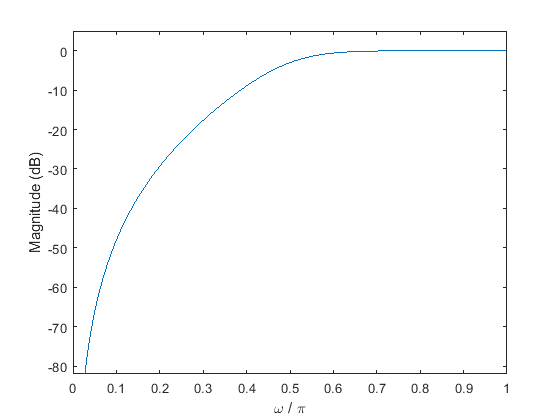
高通滤波器的幅值响应
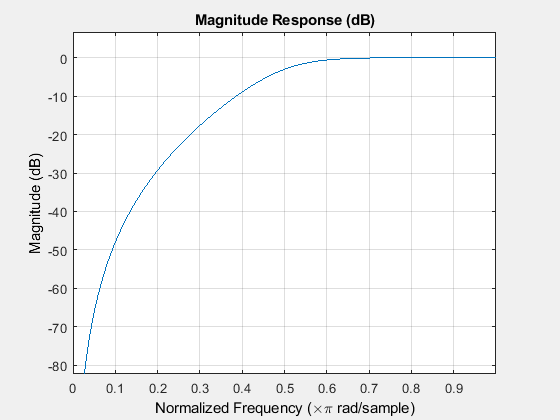
设计一个三阶高通 Butterworth 滤波器,它具有 0.5π 弧度/采样点的归一化 3-dB 频率。计算它的频率响应。用分贝表示幅值响应,并对其绘图。
[b,a] = butter(3,0.5,'high');
[h,w] = freqz(b,a);
dB = mag2db(abs(h));
plot(w/pi,dB)
xlabel('omega / pi')
ylabel('Magnitude (dB)')
ylim([-82 5])
使用 fvtool 重复计算。
fvtool(b,a)
最后
以上就是土豪巨人最近收集整理的关于matlab 求信号频率响应,频率响应 - MATLAB & Simulink - MathWorks 中国的全部内容,更多相关matlab内容请搜索靠谱客的其他文章。








发表评论 取消回复