传递函数的离散化（二）—— C实现

    传递函数要编程实现，就必须先进行离散化。前面我们介绍了一阶传函的离散化，其过程比较简单。那么对于二阶及二阶以上的传递函数怎么离散化呢？我们可以把传函转化为状态方程，这样就可以变成多个一阶的传递函数，然后再进行离散化。

一：传递函数离散化的步骤

1.传函转化为状态方程
2. 状态方程离散化

1.1 传函转化为状态方程

这里我们举一个简单的例子，把下面的传函转化为状态方程的形式：
$$G_{(s)}=\frac{2s+1}{s^2+7s+9}$$
这里我们借助matlab工具求解，代码如下：

>> num=[2 1];
>> den=[1 7 9];
>> sys=tf(num,den)

sys =
 
     2 s + 1
  -------------
  s^2 + 7 s + 9
 
Continuous-time transfer function.

>> [A B C D]=tf2ss(num,den)

A =

    -7    -9
     1     0


B =

     1
     0


C =

     2     1


D =

     0

>> 

所以状态方程为：
$$\begin{gathered} \left[\begin{array}{c}\dot{x_2}\\ \dot{x_1}\end{array}\right]=\left[\begin{array}{cc}-7& -9\\ 1& 0\end{array}\right]\left[\begin{array}{c}{x}_2\\ x_1\end{array}\right]+\left[\begin{array}{c}1\\ 0\end{array}\right]u \\ y=\left[\begin{array}{cc}2& 1\end{array}\right]\left[\begin{array}{c}{x}_2\\ x_1\end{array}\right] \end{gathered}$$
化简下：
$$\begin{gathered} \dot{x_2}=-7x_2-9x_1+u \\ \dot{x_1}=x_2 \\ y=x_1+2x_2 \end{gathered}$$

1.2 状态方程离散化

我们把上面的状态方程离散化，写出matlab function模块仿真下,代码如下：

function y = fcn(u,Ts)

persistent x1 x2;
if isempty(x1)
    x1=0;
end
if isempty(x2)
    x2=0;
end

x1 = x1 + Ts*x2;
x2 = x2 + Ts*(-9*x1-7*x2+u);
y = x1+2*x2;

end

二：传递函数离散化的仿真验证

我们把上面例子中的传递函数，状态方程和离散化的代码进行仿真验证下查看其阶跃响应：

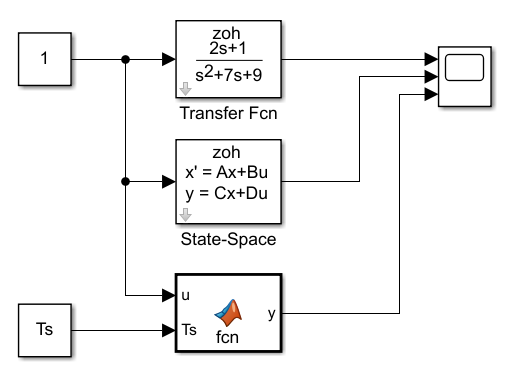
三种方式的阶跃响应结果完全重合如下：

参考模型：https://download.csdn.net/download/wanrenqi/84389722

最后

以上就是义气电源为你收集整理的传递函数的离散化（二）—— C实现的全部内容，希望文章能够帮你解决传递函数的离散化（二）—— C实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。