概述
学习笔记（3）:Verilog数字逻辑电路设计方法
- 1.Verilog语言设计思想和可综合特性
- 2.Verilog组合逻辑电路
- 2.1 数字加法器
- 2.2 数据比较器
- 2.3 数据选择器
- 2.4 数字编码器
- 2.5 数字译码器
- 2.6 奇偶校验器
- 3.时序电路
- 3.1 触发器
- 3.1.1 简单的D触发器
- 3.1.2 带复位端（清零端）D触发器：
- 3.1.3 复杂功能D触发器
- 3.1.4 T触发器
- 3.2 计数器
- 3.2.1 二进制计数器
- 3.2.2 任意模数的计数器
- 3.3 移位寄存器
- 3.4 序列信号发生器
- 4.有限同步状态机
- 来源：蔡觉平老师的Verilog课程
1.Verilog语言设计思想和可综合特性
例：用Verilog设计模256（8bits）计数器
（a）可综合程序描述方式
（b）常见的错误描述方式
同时Verilog的电路描述方式具有多样性，这也决定了对于电路设计的多样性。
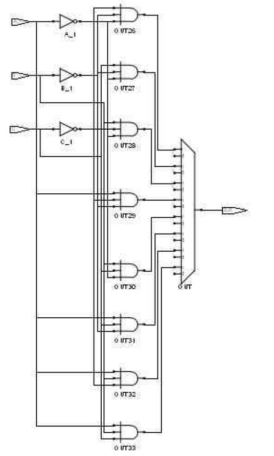
例：用Verilog设计数字多路选择器
（a）采用真值表形式的代码
（b）采用逻辑表达式形式的代码
（c）采用结构性描述的代码
2.Verilog组合逻辑电路
组合电路的特点是：电路中任意时刻的稳态输出仅仅取决于该时刻的输入，而与电路原来的状态无关。
组合电路的设计需要从以下几个方面考虑：
- 所用的逻辑器件数目最少，器件的种类最少，且器件之间的连线最简单。这样的电路称“最小化"电路；
- 其次，为了满足速度要求，应使级数尽量少，以减少门电路的延迟；电路的功耗应尽可能的小，工作时稳定可靠。
描述组合逻辑电路有四种方式：结构描述、逻辑代数、真值表、抽象描述。
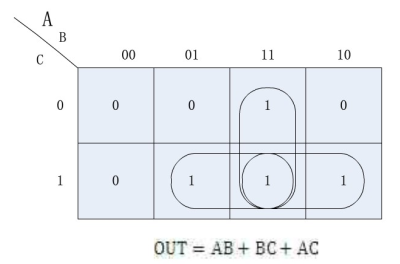
例如：设计一个3个裁判的表决电路，当两个或两个以上裁判同意时，判决器输出"1"，否则输出"0" 。
方法1：真值表方式
真值表是对电路功能最直接和简单的描述方式。根据电路的功能，可以通过真值表直接建立起输出与输入之间的逻辑关系。本例有三个输入端A、B、C和一个输出端OUT 。
| A | B | C | OUT |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
在Verilog中，可以使用“case”语句对电路进行描述性设计，根据上表设计：
方法2：逻辑代数方式
对于组合电路的另一种表达方法是逻辑代数方法。主要思想是将真值表用卡诺图表示，然后化简电路，得出逻辑函数表达式。
通过对卡诺图的化简，可以得到组合电路逻辑输出与输入之间的逻辑函数表达式：
根据逻辑函数表达式可以很方便写出采用逻辑代数描述方式的Verilog：
module desingn(OUT,A,B,C);
output OUT;
input A,B,C;
assign OUT = (A&B) | (B&C) | (A&C);
endmodule
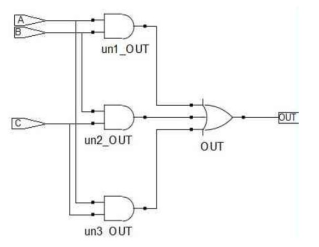
方法3：结构描述方式
结构性描述方式是对电路最直接的表示，早期的数字电路设计通常采用的原理图设计实际上就是一种结构性描述方式。
module desingn(OUT,A,B,C):
output OUT;
input A,B,C;
and U1(w1,A,B);
and U2(w2,B,C);
and U3(w3,A,C);
or U4(OUT,w1,w2,w3);
endmodule
方法4：抽象描述方式
Verilog还提供了采用抽象描述进行电路设计的方法，可以直接从电路功能出发，编写代码。例如判决器设计，将三个输入的判决相加，当判决成功时相加器之和大于1 ， 即表示投票成功。
module desingn(OUT,A,B,C);
output OUT;
input A,B,C;
wire [1:0} sum;
reg OUT;
assign sum = A + B + C;
always@(sum)
if(sum > 1)
OUT = 1;
else
OUT = 0;
endmodule
2.1 数字加法器
数字加法器是最为常用的一种数字运算逻辑，被广泛用于计算机、通信和多媒体数字集成电路中
例如：2输入1bit信号全加器。考虑了来自低位的进位那么该运算就为全加运算，实现全加运算的电路称为全加器。
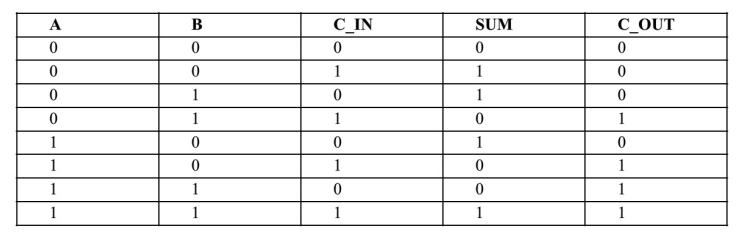
代数逻辑表示为：
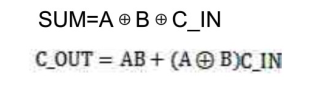
对应的电路如下：
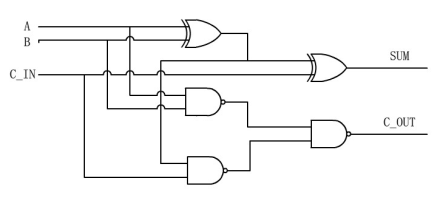
Verilog可以用不同的描述方式写出一位全加器，其综合电路是相同的，只是描述风格不同。
（1）利用连续赋值语句实现
module one_bit_fulladder(SUM, C_OUT, A, B, C_IN);
input A, B, C_IN;
output Sum, C_OUT;
assign SUM = (A ^ B) ^ C_IN;
assign C_OUT = (A & B) | ((A ^ B) & C_IN);
endmodule
（2）利用行为描述实现
module one_bit_fulladder(SUM, C_OUT, A, B, C_IN);
input A, B, C_IN;
output SUM, C_OUT;
assign {C_OUT,SUM} = A + B + C_IN;
endmodule
采用行为描述可以提高设计的效率，对于一个典型的多位加法器的行为描述设计，仅需改变代码中输入和输出信号的位宽即可，例如一个2输入8bits 加法器:
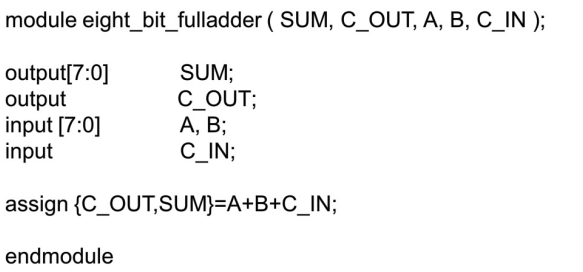
例：4位超前进位加法器
超前进位加法器是一种高速加法器，每级进位由附加的组合电路产生，高位的运算不需等待低位运算完成，因此可以提高运算速度。
根据对于输入信号位宽为N的全加器，其进位信号是：
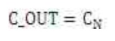
输出的加法结果是
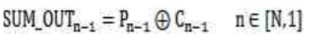
超前进位标志信号是
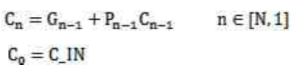
进位产生函数是
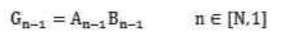
进位传输函数是
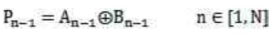
上述公式中N为加法器位数，在4位加法器中，N=4。由式可以推出各级进位信号表达式，并构成快速进位逻辑电路。
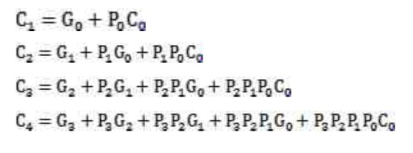
4位超前进位加法器的电路图如下
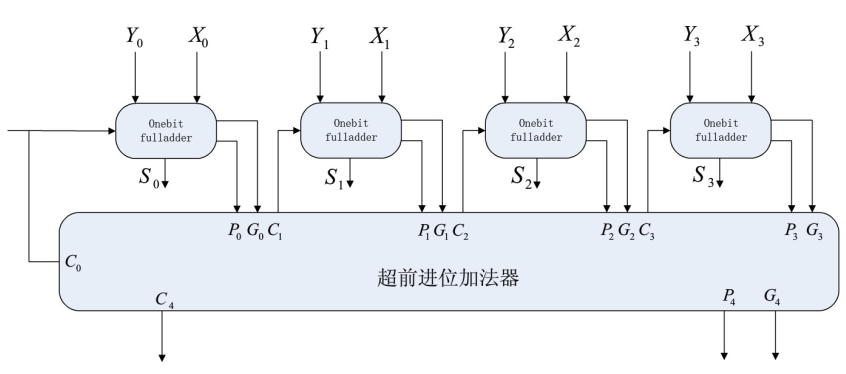
4位超前进位加法器的Verilog代码：
2.2 数据比较器
数据比较器是用来对两个二进制数的大小进行比较，或检测是否相等的逻辑电路。数据比较器包含两个部分：一是比较两个数的大小；二是检测两个数是否一致。
例：4位数值比较器
多位数值比较器的比较过程是由高位到底位逐位进行比较，而且只有在高位相等时，才进行低位比较。4位数值比较器中进行A3A2A1A0和B3B2B1B0的比较时，应首先比较最高位A3和B3。如果A3>B3，那么不管其它几位数为何值，结果为A>B；若A3<B3，为A< B。如果A3=B3，就必须通过比较低一位A2和B2来判断A和B的大小。如果A2=B2，还必须通过比较更低一位A1和B1来判断，直到最后一位的比较。如果完全相等，则由前一级结果C(级联输入)确定。
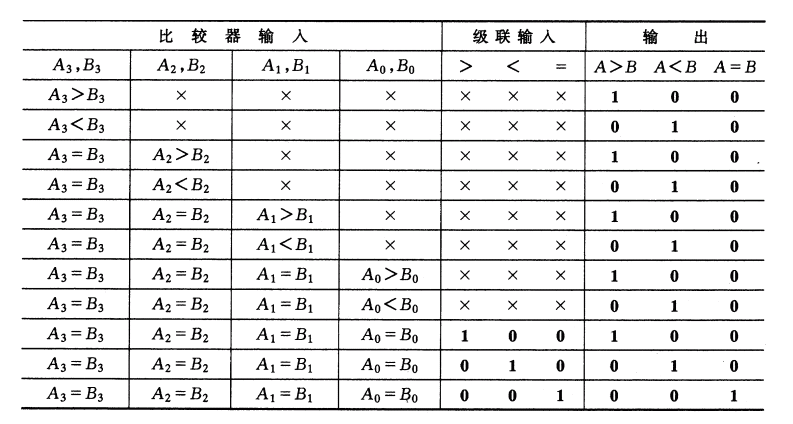
module four_bits_comp(F, A, B,C);
parameter comp_width = 4;
output [2:0] F;
input [comp_width-1:0] A;
input [comp_width-1:0] B;
ref [2:0] F;
always@(A or B or C)
if(A>B)
F = 3'b100;
else if(A<B)
F = 3'b001;
else
F = C;
endmodule
2.3 数据选择器
数据选择器又称多路选择器(Multiplexer,简称MUX)，它有n位地址输入、2n位数据输入，1位数据输出。每次在输入地址的控制下，从多路输入数据中选择一路输出，其功能类似于一个单刀多掷开关，如图:
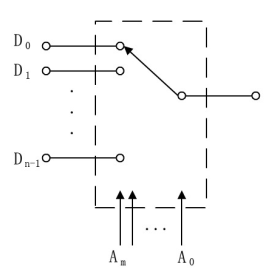
例，8选1数据选择器
8选1数据选择器可以由多个2选1选择器组成：
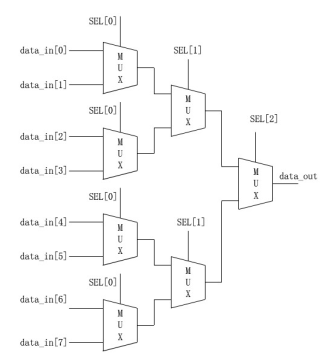
（1）多个2选1数据选择器的结构级描述
module mux8to1(d_out, d_in, sel);
output d_out;
input[7:0] d_in;
input [2:0] sel;
wire[3:0] w1;
wire[1:0] w2;
assign w1 = sel[0] ? {d_in[7], d_in[5], d_in[3], d_in[1]} : {d_in[6], d_in[4], d_in[2], d_in[0]};
assign w2 = sel[1] ? {w1[3], w1[1]} : {w1[2], w1[0]};
assign d_out = sel[2] ? w2[1] : w2[0];
endmodule
（2） 抽象描述方式
对于多路选择器的设计，可以通过“case”语句进行设计。
2.4 数字编码器
用文字、符号或数码表示特定对象的过程称为编码。在数字电路中用二进制代码表示有关的信号称为二进制编码。实现编码操作的电路叫做编码器。
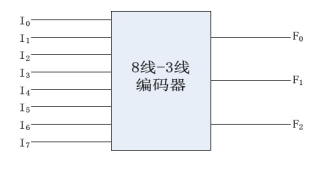
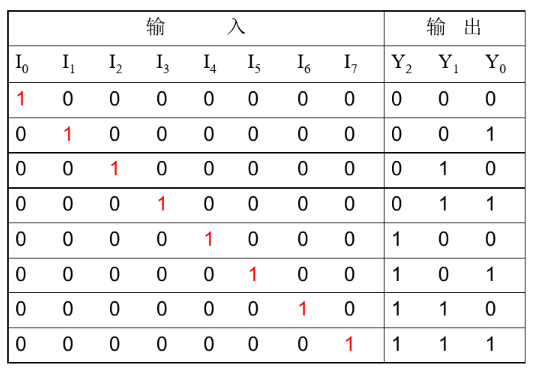
例：3位二进制8-3线编码器
用n位二进制代码对N=2n个一般信号进行编码的电路，叫做二进制编码器。
例如n=3，可以对8个一般信号进行编码。这种编码器有一个特点：任何时刻只允许输入一个有效信号，不允许同时出现两个或两个以上的有效信号。
如下框图：
真值表：
module 8to3(F, I）；
output [2:0] F;
input [7:0} I;
reg [2:0] F;
always@(I)
case(I):
8'b00000001:F=3'b000;
8'b00000010:F=3'b001;
8'b00000100:F=3'b010;
8'b00001000:F=3'b011;
8'b00010000:F=3'b100;
8'b00100000:F=3'b101;
8'b01000000:F=3'b110;
8'b10000000:F=3'b111;
default: F= 3'bx;
endcase
endmodule
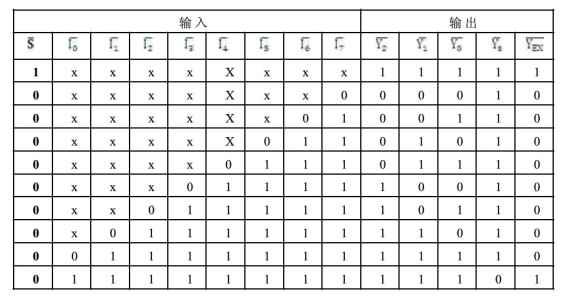
例：8线-3线优先编码器
二进制编码器电路要求任何时刻只有一个输入有效，若同时有两个或更多个输入信号有效时，将造成输出混乱状态，因此在使用过程中有一定局限性。为了克服对于输入信号的要求，一种方法是采用优先编码器。优先编码器允许多个输入信号同时有效，但它只按其中优先级别最高的有效输入信号编码，对级别低的输入信号不予理睬。
功能表：
例：二进制转化十进制8421 BCD编码器
将十进制数0、1、2、3、4、5、6、7、8、9等十个信号编成二进制代码的电路叫做二进制转化十进制编码器。它的输入是代表0-9这10个数字的状态信息，有效信号为1（即某信号为1时，则表示要对它进行编码），输出是相应的BCD码，因此也称10线一4线编码器。它和二进制编码器特点一样，任何时刻只允许输入一个有效信号。
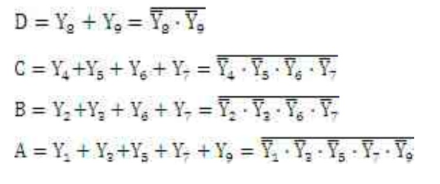
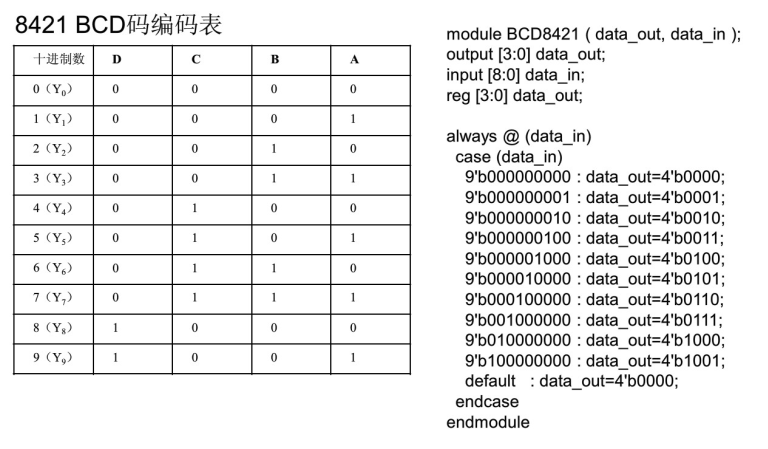
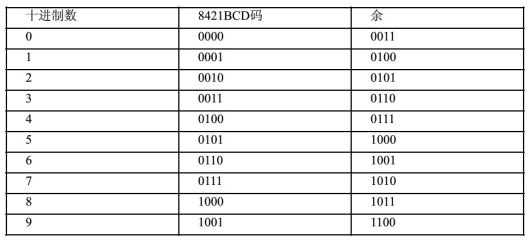
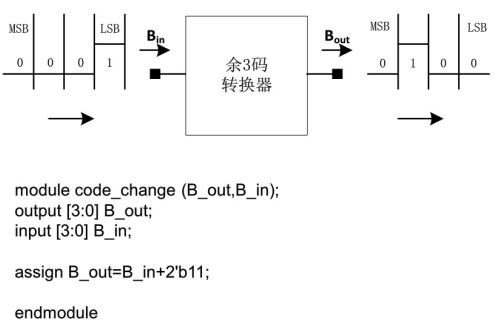
例：8421BCD十进制余3编码器
和8421BCD编码一样，余3码是也一种BCD编码，这种编码的特点是，余3码作十进制加法运算的时候，若2数之和是10，正好等于二进制数的16，于是便从高位自动产生进位信号，因此可以使用余3码。
余3码编码表：
2.5 数字译码器
译码是编码的逆过程，它将二进制代码所表示的信息翻译成相应的状态信息。实现译码功能的电路成为译码器。
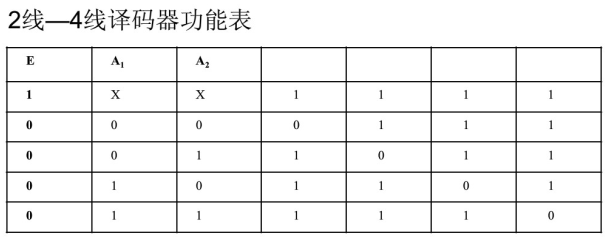
图是2线-4线译码器的逻辑电路及逻辑符号。图中A1,A0为地址输入端，A1为高位。非Y0 - 非Y3为状态信号输出端，"非"表示低点平有效。E为使能端（或称选通控制端），低电平有效。当E = 0时，允许译码器工作，非Y0 - 非Y3中只允许一个为有效电平输出；当E = 1时，禁制译码器工作，所有输出均为高电平。
一般使能端有两个用途：一是可以引入选通脉冲，以抑制冒险脉冲的发生；二是可以用来扩展输入变量数（功能扩展）。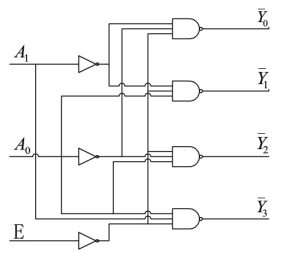
2.6 奇偶校验器
奇偶校验器的功能是检测数据中包含"1"的个数是奇数还是偶数。在计算机和一些数字通信系统中，常用奇偶校验器来检查数据传输和数码记录中是否存在错误。
奇偶校验包含两种方式：奇校验和偶校验。奇校验保证传输数据和校验位中"1"的总数为奇数。如果数据中包含奇数个"1"，则校验位置“0" ，如果数据中包含偶数个"1"，则校验位置"1"。偶校验保证传输数据和校验位中"1"的总数为偶数。如果数据中包含奇数个"1"，则校验位置"1"，如果数据中包含偶数个"1"，则校验位置"0" 。
奇偶校验只能检测部分传输错误，它不能确定错误发生在哪位或哪几位，所以不能进行错误校正。当数据发生错误时只能重新发送数据。
例：8bits奇偶校验器
8bits奇偶校验器的原理图如图所示：
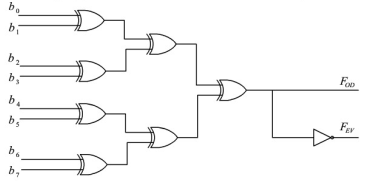
图中，校验器的输入b0 - b7由7bits数据和1 bit校验位组成。FOD为判奇输出，FEV为判偶输出。当采用奇校验时,FOD = 1,FEV = 0；当采用偶校验时，FOD=O, FEV = 1。
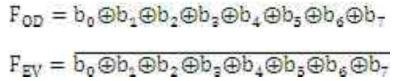
3.时序电路
与组合逻辑电路不同，时序逻辑电路的输出不仅与当前时刻输入变量的取值有关，而且与电路的原状态，即与过去的输入情况有关。
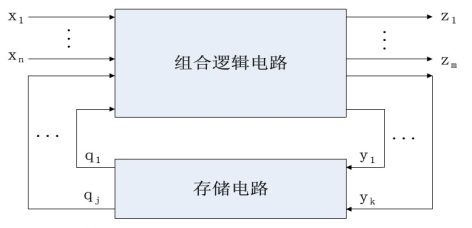
时序逻辑电路有两个特点：
（1）时序逻辑电路包括组合逻辑电路和存储电路两部分，存储电路具有记忆功能，通常山触发器组成；
（2）存储电路的状态反馈到组合逻辑电路输入端，与外部输入信号共同决定组合逻辑电路的输出。
同步时序电路设计流程：
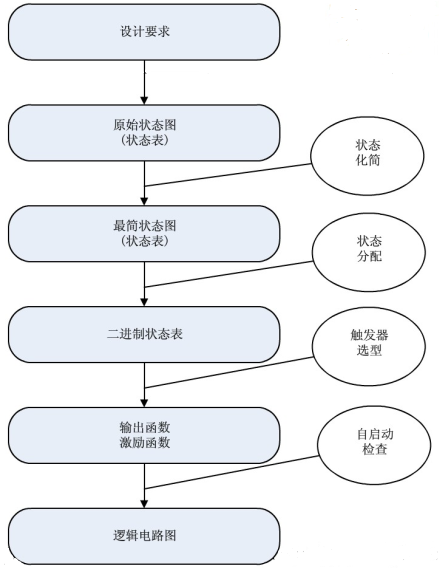
例：用verilog设计一个"111"的序列检测器，当输入三个或三个以上“ 1 "时，电路输出为1，否则为0。
（1）状态转移图方法
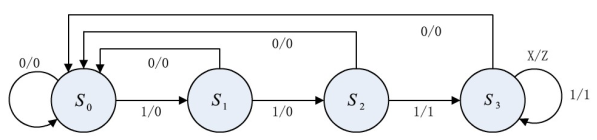
S0：初始状态，表示电路还没有收到一个有效的1。
S1：表示电路收到了一个1。
S2：表示电路收到了连续两个1。
S3：表示电路收到了连续三个1。
电路图：
module check(z, x, clk);
parameter s0 = 2'b00, s1 = 2'b01, s2 = 2'b10, s3 = 2'b11;
output z;
input x, clk;
reg[1:0} state, next_state;
reg z;
always@(posedge clk)
case(state)
s0:if(x)
begin
next_state <= s1;
z = 0;
end
else
begin
next_state <= s0;
z = 0;
end
s1:if(x)
begin
next_state <= s2;
z = 0;
end
else
begin
next_state <= s0;
z = 0;
end
s2:if(x)
begin
next_state <= s3;
z = 1;
end
else
begin
next_state <= s0;
z = 0;
end
s0:if(x)
begin
next_state <= s3;
z = 0;
end
else
begin
next_state <= s0;
z = 0;
end
endcase
always@(posedge clk)
state <= next_state;
endmodule
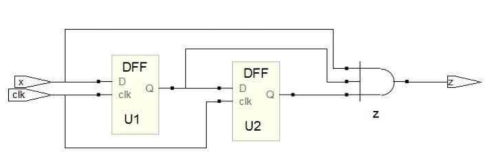
（2）基于状态化简的结构性描述方法
对状态转移图化简，仅剩三个状态，需要两位二进制表示，即需要两个D触发器储存状态。设Q1表示高位寄存器的输出，Q0表示低位寄存器的输出。将状态的跳转以及输出Z用卡诺图表的形式示出，如下：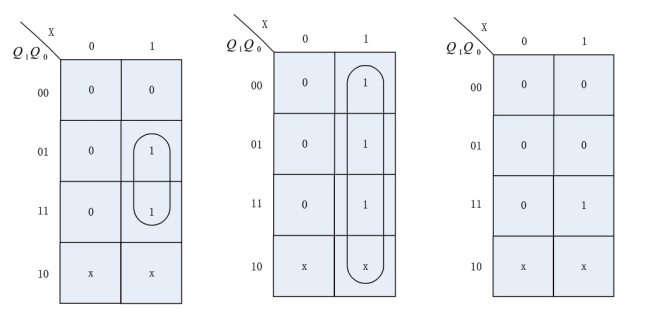
由卡诺图可以得出电路的输出方程和状态方程：
Q1n+1 = Q1
Q0n+1 = X
Z = Q1Q0X
//D触发器模块
module DFF(Q, D, clk);
output Q;
input D, clk;
reg Q;
always@(posedge clk)
Q <= D;
endmodule
//序列检测模块
module check(z, x, clk);
output z;
input x,clk;
wire w1,w2;
DFF U1(.clk(clk), .D(x), .Q(w1));
DFF U2(.clk(clk), .D(w1), .Q(w2));
assign z = x&w1&w2;
endmodule
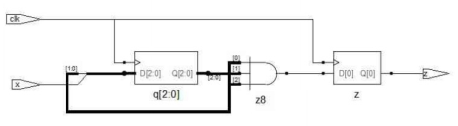
（3）Verilog HDL抽象性描述方法
在Verilog中还可以对电路进行抽象的描述。实现序列“111"的检测，可以使用一个三位的移位寄存器，将输出x作为移位寄存器的输出，当寄存器中为111时，输出Z为1。
module check(z, x, clk);
output z;
input x,clk;
reg[2:0] q;
reg z;
always@(posedge clk)
q <= {q[1:0], x};
always@(posedge clk)
if(q == 3'b111)
z = 1;
else
z = 0;
endmodule
3.1 触发器
触发器是时序电路的最基本电路单元，主要有D触发器、JK触发器、 T触发器和RS触发器等。根据功能要求的不同 ， 触发器还具有置位、复位、使能、选择等功能。
3.1.1 简单的D触发器
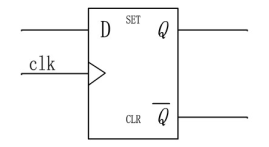
| clk | D | Qn | Qn+1 |
|---|---|---|---|
| 0 | x | 0 | 0 |
| 0 | x | 1 | 1 |
| 1 | x | 0 | 0 |
| 1 | x | 1 | 1 |
| ↑ | 0 | 0 | 0 |
| ↑ | 0 | 1 | 0 |
| ↑ | 1 | 0 | 1 |
| ↑ | 1 | 1 | 1 |
module DFF(Q, D, clk);
output Q;
input D, clk;
reg Q;
always@(posedge clk)
Q <= D;
endmodule
输入端的数据D在时钟clk的上升沿被送入触发器，使得Q=D。其特征方程可描述为Qn+1 = Dn。
3.1.2 带复位端（清零端）D触发器：
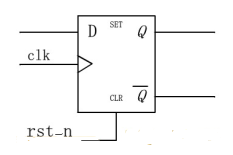
同步清0的触发器：
module DFF_rst(q, clk, rst_n, d);
output q;
input clk,rst_n,d;
reg q;
always@(posedge clk)
if(!rst_n)
q<=0;
else
q<=d;
endmodule
异步清0的触发器：
module DFF_rst(q, clk, rst_n, d);
output q;
input clk,srst_n,d;
reg q;
always@(posedge clk or rst_n)
if(!rst_n)
q<=0;
else
q<=d;
endmodule
3.1.3 复杂功能D触发器
同步清0，置1和异步清0，置1共同在一个触发器的复杂D触发器。
module DFF(q, qb, clk, rst_n1, set1, rst_n2, set2, data_in);
output q, qb;
input clk, rst_n1,rst_n2, set1,set2, data_in;
reg q,qb;
always@(posedge clk)
if(!rst_n1)
q<=0;
else
q<=data_in;
always@(posedge clk or rst_n2)
if(!rst_n2)
q<=0;
else
q<=data_in;
endmodule
3.1.4 T触发器
T触发器的逻辑符号如下，T触发器的功能：当时钟的有效边沿到来时，如果T=1，则触发器翻转；如果T=0，则触发器的状态保持不变。R为复位端，异步复位，低电平有效。
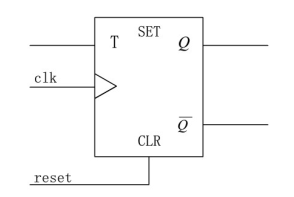
module TFF(d, t, clk, rst_n);
output d;
input t, clk, rst_n;
reg d;
always@(posedge clk or rst_n)
if(!rst_n)
d <= 1'b0;
else if(t)
d <= ~d;
endmodule
3.2 计数器
3.2.1 二进制计数器
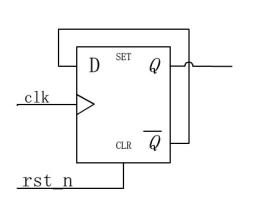
module comp2(q, clk, rst);
output q;
input clk,rst;
reg q;
always@(posedge clk or rst_n)
if(!rst)
q <= 1'b0;
else
q <= ~q;
endmodule
3.2.2 任意模数的计数器
任意模值M的计数器，第一步需要确定计数器所需要触发器个数。N个触发器对应了2N个状态。应有2N > M任意模值计数器选取满足条件的最小N，N为计数器中触发器的个数。有两种方法实现 ： 反馈清零法和反馈置数法。
//反馈清零法设计的模11计数器
module comp11(count, clk, rst);
output[3:0] count;
input clk,rst;
reg[3:0] count;
always@(posedge clk)
if(rst)
count <= 4'b0000;
else
if(count == 4'b1010)
count <= 4'b0000;
else
count <= count + 1;
endmodule
3.3 移位寄存器
移位寄存器可以用来实现数据的串并转换，也可以构成移位行计数器，进行计数、分频，还可以构成序列码发生器、序列码检测器等，它也是数字系统中应用非常广泛的时序逻辑部件之一。
例：环形移位寄存器
N位环型寄存器由N个移位寄存器组成，可以实现环型移位
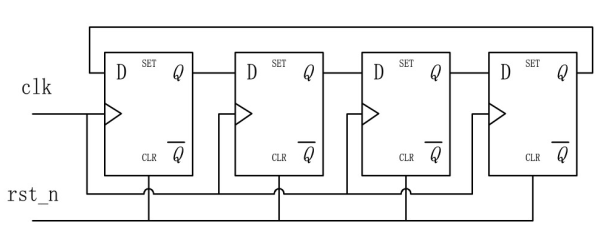
将每个寄存器的输出作为下一位寄存器的输入，并将高位寄存器的输出作为循环的输入。
module shiftregist(D, clk, rst_n);
parameter shiftregist_width = 4;
output [shiftregist_width-1:0] D;
input clk,rst_n;
reg [shiftregist_width-1:0] D;
always@(posedge clk)
if(!rst_n)
D<=4'b0000;
else
D<={D[shiftregist_width-2:0], D[shiftregist_width-2:1]};
endmodule
3.4 序列信号发生器
序列信号是数字电路系统中常用的功能单元，按照序列循环长度M和触发器数目n的关系一般可分为三种：
（1） 最大循环长度序列码，M=2n;
（2） 最长线形序列码（m序列码），M=2n-1;
（3） 任意循环长度序列码，M<2n。
序列信号发生器是能够产生一组或多组序列信号的时序电路，它可以由纯时序电路构成，也可以由包含时序和组合逻辑的混合电路构成。
例：设计一个产生10011序列的信号发生器
- 方法（1）：由移位寄存器构成
由于移位寄存器输入和输出信号之间没有组合电路，不需要进过组合逻辑的反馈运算，因此这种序列产生电路的工作频率很高。 缺点是移位寄存器长度取决于序列长度，因此占用电路的面积很大。
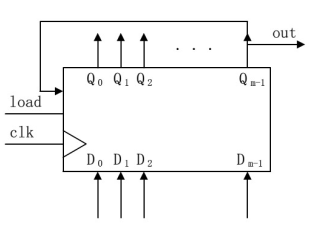
module maker(out, clk, load, D);
parameter M=6;
output out;
input clk,load;
input [M-1:0] D;
reg [M-1:0] Q;
initial Q=6'b10011;
always@(posedge clk)
if(load)
Q<=D;
else
Q<={Q[M-2:0], Q[M-1]};
assign out=Q[M];
endmodule
方法（2）：由移位寄存器和组合逻辑电路构成
反馈移位型序列码发生器的结构框图如图所示，它由移位寄存器和组合逻辑网络组成，从移位寄存器的某一输出端可以得到周期性的序列码。
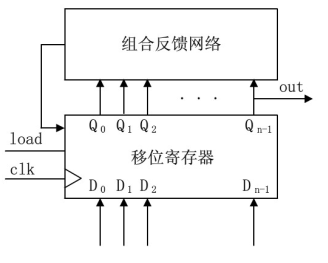
其设计按以下步骤进行：
（1）根据给定序列信号的循环周期M，确定移位寄存器位数n，2n-1<M≤2n。
（2）确定移位寄存器的M个独立状态。将给定的序列码按照移位规律每n位一组，划分为M个状态。若M个状态中出现重复现象，则应增加移位寄存器位数。用n + 1位再重复上述过程，直到划分为M个独立状态为止。
（3）根据M个不同的状态列出移位寄存器的态序表和反馈函数表，求出反馈函数F的表达式。
（4）检查自启动性能。
与上面的序列信号发生器相比，各个寄存器的输出需要经过反馈网络，然后才连接到移位寄存器的输入端。因此，电路的速度必然下降，但反馈网络的好处在于它可以节省寄存器。
对于“ 1001 1 1 "序列的信号发生器。
首先，确定所需移位寄存器的个数n。因M = 6，故n 3。
然后，确定移位寄存器的六个独立状态。
按照规律每三位一组，划分六个状态为100,001,011,111,111,110。其中状态111重复出现，故取n=4，并重新划分状态，得到：1001、0011、0111、1111、1110、1100。因此确定n =4。
第三，列态序表和反馈激励函数表，求反馈函数F的表达式。
首先列出态序表，然后根据每一状态所需要的移位输入即反馈输入信号，列出反馈激励函数表，如下表所示。求得反馈激励函数：
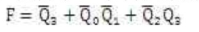
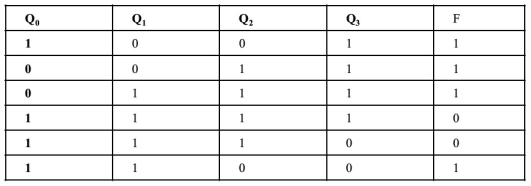
//反馈移位型序列信号发生器
module maker(out, clk, load, D);
parameter M=4;
output out;
input clk,load;
input [M-1:0] D;
reg {M-1:0] Q;
wire w1;
always@(posedge clk)
if(load)
Q<=D;
else
Q<={Q[M-2:0],ww1};
assign w1 = (~Q[3])|((~Q[1])&(~Q[0]))|(Q[3]&(~Q[2]));
assign out =Q[M-1];
endmodule
方法（3）：由计数器构成
计数型序列信号发生器和反馈型序列信号发生器大体相同，它们都是由时序电路和组合电路两部分构成。不同在于，反馈型序列信号发生器的时序状态由移位寄存器产生，输出取寄存器的最高位；而在计数型序列信号发生器中，采用计数器代替移位寄存器产生时序状态，输出由组合电路产生。
计数型的好处在于，计数器的状态设置与输出序列没有直接关系，不需要像上面一样，根据输出确定状态。只需要将反馈网络设计好就可以了。因此计数结构对于输出序列的更改比较方便，而且只要连接到不同的反馈网络，它可以同时产生多组序列码。
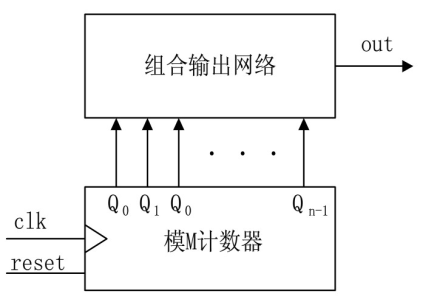
设计过程分为两步：
第一，根据序列码的长度M设计模M计数器，状态可以自定；
第二，按计数器的状态转移关系和序列码的要求设计组合输出网络。对于“ 100111 "序列的信号发生器。序列信号的M值为6，因为需选用模6的计数器。计数器的状态选择从000到101,可得下表。
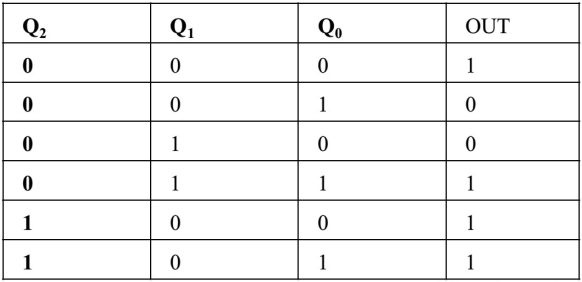
由真值表可画出卡诺图，得到输出函数：
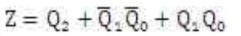
如下代码：
module maker(OUT, clk, reset);
parameter M=3;
input clk,reset;
reg [M-1:0] counter;
always@(posedge clk)
if(!reset)
counter <= 3'b000;
else
counter <= counter + 1;
assign OUT = counter[2] | ((~counter[1])&(~counter[0])) | (counter[1]&counter[0]);
endmodule
例：设计伪随机码发生器
随机码是一种变化规律与随机码类似的二进制代码，可以作为数字通信中的一个信号源，通过信道发送到接收机，用于检测数字通信系统错码的概率，即误码率。
在传统的数字电路设计中，伪随机序列信号发生器是用移位存型计数器来实现的，反馈网络输入信号从移位寄存器的部分输出端(QN-1 ~ Q0)中取出，它的输出端F反馈到移位寄存器的串行输入端。
通过不同的反馈网络，可以形成不同的移存型计数器。以m序列码为例，反馈函数如下表所示，表中的N 是触发器的级数，F是反馈函数的列表。
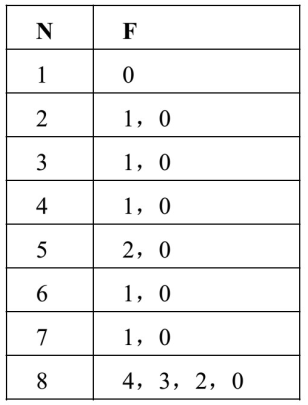
例如N =4，则反馈函数如下：
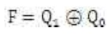
以N =4为例，在15位最长线性序列移存型计数器中，有一个由"0000"构成的死循环，为了打破死循环，可以修改式为:
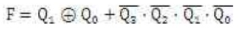
根据N=4的最长线性序列移位寄存器计数器：
module signal(out, clk, load_n, D_load);
output out;
input load_n,clk;
input [3:0] D_load;
reg [3:0] Q;
wire F;
always@(posedge clk)
if(~load_n)
Q<=D_load;
else
Q<={Q[2:0],F};
assign F = (Q[1]^Q[0]) | (~Q[3]&~Q[2]&~Q[1]&~Q[0]);
assign out = Q[3];
endmodule
4.有限同步状态机
有限状态机是时序电路的通用模型，任何时序电路都可以表示为有限状态机。有限状态机从本质上讲是由寄存器与组合逻辑构成的时序电路，各个状态之间的转移总是在时钟的触发下进行的，状态信息存储在寄存器中。因为状态的个数是有限的所以称为有限状态机。
同其它时序电路一样，有限状态机也是由两部分组成：存储电路和组合逻辑电路。存储电路，用来生成状态机的状态；组合逻辑电路，用来提供输出以及状态机跳转的条件。
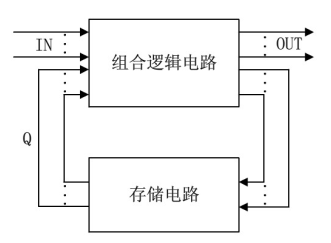
根据输出信号的产生方式，有限状态机可以分为米利型（Mealy）和摩尔型（Moore）两类。Mealy型状态机的输出与当前状态和输入有关系，Moore型状态机的输出仅依赖当前状态而与输入无关。
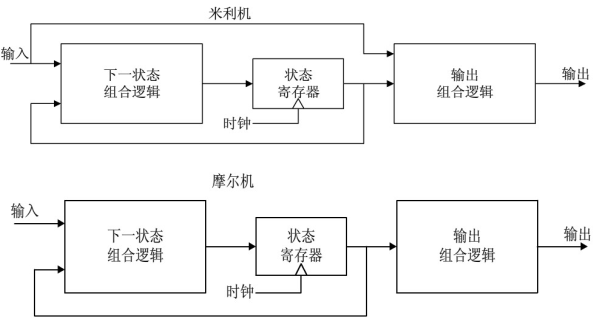
状态机编码方式很多，由此产生的电路也不相同，常见的编码方式有三种：二进制编码、格雷编码和一位独热编码。
（1）二进制编码：状态寄存器是由触发器组成的。N个触发器可以构成2n个状态。二进制编码的优点是使用的触发器个数较少，节省资源；缺点是状态跳转时可能有多个bit位同时变化，引起毛刺，造成逻辑错误。
（2）格雷编码：格雷编码和二进制编码类似。格雷编码状态跳转时只有一个 bit位发生变化，减少了产生毛刺和一些暂态的可能。
（3）One hot编码：是对于n个状态采用n个bit位来编码，每个状态编码中只有一个bit位为1，如：0001，0010，0100，1000。One hot编码增加了使用触发器的个数，但是这种编码方便译码，可以有效地节省和化简组合电路。
在Verilog中，有限状态机的写法较多，常用的有两段式和三段式两种。
（1）状态机两段式描述方式：
//第一个进程，同步时序always模块，格式化描述次态寄存器迁移到现态寄存器
always@(posedge clk or negedge rst_n) //异步复位
if(!rst_n)
current_state <= IDLE;
else
current_state <= next_state; //注意，使用的是非阻塞赋值
//第二个进程，组合逻辑always模块，描述状态转移条件判断
always@(current_state) //电平触发
begin
next state = x; //要初始化，使得系统复位后能进入正确的状态
case(current_state)
S1:if(...)
next_state=S2; //阻塞赋值
out1<= 1'b1;//注意是非阻塞逻辑
...
endcase
end
（2）状态机三段式描述方式：
//第一个进程，同步时序always模块，格式化描述次态寄存器迁移到现态寄存器
always @ (posedge clk or negedge rst_n) //异步复位
if(!rst_n)
current_state <= IDLE;
else
current_state <= next_state;//注意，使用的是非阻塞赋值
//二个进程，组合逻辑always模块，描述状态转移条件判断
always @ (current_state) //电平触发
begin
next_state=x; //要初始化，使得系统复位后能进入正确的状态
case(current_state)
S1:if(...)
next_state=S2; //阻塞赋值
...
endcase
end
//第三个进程，同步时序always模块，格式化描述次态寄存器输出
always@(posedge clk or negedge rst_n)
...//初始化
case(next_state)
S1:
out1 <= 1'b1；//注意是非阻塞逻辑
S2:
out2 <= 1'b1;
default:... //default的作用是免除综合工具综合出锁存器。
endcase
end
//三段式不一定要写三个always块，如果状态机更为复杂，always块也会相应增加。
例：设计顺序脉冲发生器
顺序脉冲发生器又称脉冲分配器，它将高电平的脉冲依次分配到不同输出上。保证在每个时钟内只有一路输出上是高电平脉冲，不同时钟上脉冲电平依次出现在所有输出。
以4位顺序脉冲发生器为例，它有四路输出W0W1W2W3,每路输出上高电平脉冲依次出现，输出在1000，0100，0010，0001之间循环。4位顺序脉冲发生器的状态转移图。如图，它由4 个状态构成，每个状态中“1"的个数都是 1个，表示每个时钟周期内只有一路输出端为高电平（脉冲），而且是轮流出现，因此生成顺序脉冲信号。
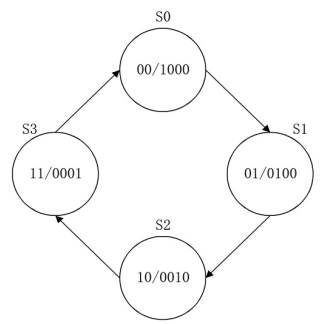
对四状态机编码时，只需要两位二进制编码即可：
module state4(out, clk);
output [3:0] out;
input clk;
reg [3:0] out;
reg [1:0] state, next_state;
always@(state)
case(state)
2'b00:
begin
out <= 4'b1000;
next_state <= 2'b01;
end
2'b01:
begin
out <= 4'b0100;
next_state <= 2'b10;
end
2'b10:
begin
out <= 4'b0010;
next_state <= 2'b11;
end
2'b00:
begin
out <= 4'b0001;
next_state <= 2'b010;
end
endcase
always@(posedge clk)
state <= next_state;
endmodule
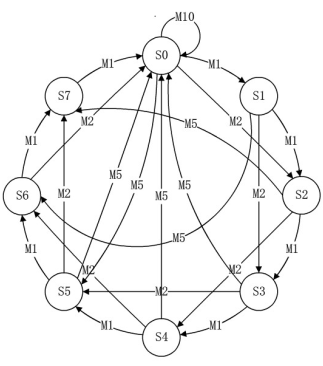
例：设计一个卖报机，报纸价钱八角，纸币有1角，2角，5角，一元。该卖报机不考虑投币为大额面值等特殊情况。下图是卖报机的状态转移图，图中S0 ~ S7 为状态机的8个状态，角标代表己投币的总合，如SO代表没有投币，S1代表己投入1 角，依此类推。M代表输入，M1表示投入1角硬币，M2代表投入2角硬币，M5代表投入5角硬币，M10代表投入一元。
Verilog代码：
//data_out=1表示给出报纸，data_out_return=1表示找回1角硬币，data_out_return2=1表示找回2角硬币
module auto_sellor(current_state,data_out, data_out_return1, data_out_retum2, clk, rst_n, data_in);
parameter state_width = 3, data_in_width = 3;
output [state_width-1:0] current_state;
output data_out, data_out_return1, data_out_return2;
input [data_in_width-1:0] data_in;
input clk, rst_n;
reg [state_width-1 :0] current_state, next_state;
reg data_out, data_out_return1, data_out_return2;
always@(current_state or rst_n)
if (!rstn)
next_statec=0;
else
case(current_state)
3'b000:
case(data_in)
3'b000:
begin
next_state <= 3'b000;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b001:
begin
next_state <= 3'b001;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b010:
begin
next_state <= 3'b010;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b011:
begin
next_state <= 3'b101;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b100:
begin
next_state <= 3'b000;
data_out <=1'b1;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b1;
end
endcase
3'b001:
case(data_in)
3'b000:
begin
next_state <= 3'b001;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b001:
begin
next_state <= 3'b010;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b010:
begin
next_state <= 3'b011;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b011:
begin
next_state <= 3'b110;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
endcase
3'b010:
case(data_in)
3'b000:
begin
next_state <= 3'b010;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b001:
begin
next_state <= 3'b011;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b010:
begin
next_state <= 3'b100;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b011:
begin
next_state <= 3'b111;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
endcase
3'b011:
case(data_in)
3'b000:
begin
next_state <= 3'b011;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b001:
begin
next_state <= 3'b100;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b010:
begin
next_state <= 3'b101;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b011:
begin
next_state <= 3'b000;
data_out <=1'b1;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
endcase
3'b100:
case(data_in)
3'b000:
begin
next_state <= 3'b000;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b001:
begin
next_state <= 3'b101;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b010:
begin
next_state <= 3'b110;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b011:
begin
next_state <= 3'b000;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
endcase
3'b101:
case(data_in)
3'b000:
begin
next_state <= 3'b101;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b001:
begin
next_state <= 3'b110;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b111:
begin
next_state <= 3'b011;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b011:
begin
next_state <= 3'b000;
data_out <=1'b1;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b1;
end
endcase
3'b110:
case(data_in)
3'b000:
begin
next_state <= 3'b110;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b001:
begin
next_state <= 3'b111;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b010:
begin
next_state <= 3'b000;
data_out <=1'b1;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
endcase
3'b111:
case(data_in)
3'b000:
begin
next_state <= 3'b111;
data_out <=1'b0;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
3'b001:
begin
next_state <= 3'b000;
data_out <=1'b1;
data_out_return1 <=1'b0;
data_out_return2 <= 1'b0;
end
endcase
always@(posedge clk ir rst_n)
if(!rst_n)
current_state <= 3'b000;
else
current_state <= next_state;
endmodule
例："11010"序列检测器
序列检测器就是将一个指定的序列从数字码流中检测出来。当输入端出现序列11010时，输出为1，否则输出为0。在此不考虑重复序列，即出现指定序列后就重新开始序列检测，不再考虑以前的数据。规定数据从右端输入，即按照1-1-0-1-0的顺序输入。该序列检测器的状态转移图如下：
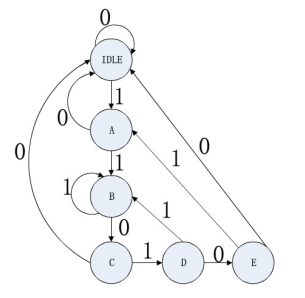
module seqdet(dout,din,restn,clk);
parameter IDLE = 3'd0, A = 3'd1, B = 3'd3, C = 3'd4, E = 3'd5;
output dout;
input din,rstn,clk;
reg[2:0] state,next_state;
wire dout;
assign dout = (state==E)?1:0;
always@(posedge clk or negedge rstn)
if(!rstn)
state = IDLE;
else
case(state)
IDLE:
if(din)
next_state = A;
else
next_state = IDLE;
A:
if(din)
next_state = B;
else
next_state = IDLE;
B:
if(din)
next_state = B;
else
next_state = C;
C:
if(din)
next_state = D;
else
next_state = IDLE;
D:
if(din)
next_state = B;
else
next_state = IDLE;
E:
if(din)
next_state = IDLE;
else
next_state = A;
default:
next_state = IDLE;
endcase
always@(posedge clk)
state <= next_state;
endmodule
来源：蔡觉平老师的Verilog课程
最后
以上就是复杂飞机为你收集整理的Verilog学习笔记（3）:Verilog数字逻辑电路设计方法1.Verilog语言设计思想和可综合特性2.Verilog组合逻辑电路3.时序电路4.有限同步状态机来源：蔡觉平老师的Verilog课程的全部内容，希望文章能够帮你解决Verilog学习笔记（3）:Verilog数字逻辑电路设计方法1.Verilog语言设计思想和可综合特性2.Verilog组合逻辑电路3.时序电路4.有限同步状态机来源：蔡觉平老师的Verilog课程所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复