matlab plot拟合_从零开始的matlab学习笔记——（26）二项分布与泊松分布

matlab应用——求极限，求导，求积分，解方程，函数绘图，三维图像，拟合函数....更多内容尽在个人专栏：matlab学习

上一节我们说了说怎么用matlab求微分方程，这一节我们再来聊聊微分方程在统计概率方面的一些应用

二项分布：

二项分布这个大家在高中都学过，我们再来复习一下定义（还是找的百度百科）：

二项分布是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。

公式:

在matlab中我们有这样一个函数binopdf，是针对二项分布的相关操作

1、可以求值：

binopdf(k,n,p)

三个参数，一共进行n次，事件发生了k次，每次概率为p

比如

px=binopdf(45,100,0.5)

答案

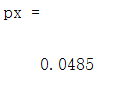
2、可以绘制概率密度曲线

x=1:1:100;

p=binopdf(x,100,0.5);

plot(x,p);

title('二项分布')

效果图：

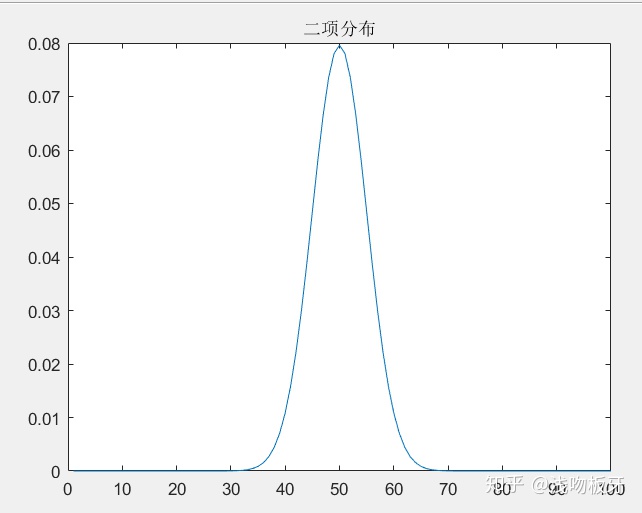
3、可以求最值

x=1:100;

p=binopdf(x,100,0.5);

[ans,pos]=max(p)%取x=pos时，ans取最大

答案：

泊松分布：

泊松分布由二项分布演进而来，可以粗略的认为是二项分布求极限之后的结果

我们先看一下定义（大概就是这个意思）：

单位时间内，事物平均发生m次，每次事件发生互相独立，且概率相等，求单位时间内发生k次的概率分布

公式:

推导过程涉及到二项分布求极限（百度百科说的还是挺清晰的）

matlab中的poisspdf函数支持泊松分布的相关操作：

1、可以求值：

poisspdf(k,m)

两个参数，单位时间内平均发生m次，求单位时间内发生k次的概率

比如

px=poisspdf(3,6) %平均6次，发生3次的概率

答案

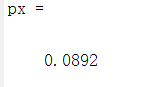
2、可以绘制概率密度曲线

x=0:1:20

p=poisspdf(x,6)%单位时间内平均发生6次，求发生x次的泊松概率

plot(x,p)

title('泊松分布')

ylabel('$p=frac{5^{x}}{x!}e^{-5}$','Interpreter','latex','FontSize',15)

效果图：

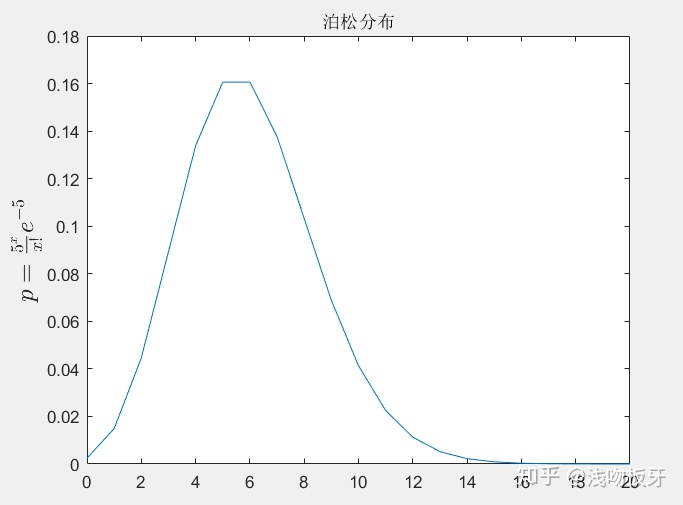
tips:

这里补充一点内容，有些LaTeX符号在matlab中引用需要特别说明，所以为了保险起见，大家直接复制这一行代码，根据自己需要修改即可：

title（或者其它你想用的函数）('$你想写的LaTeX符号$','Interpreter','latex','FontSize',字号)

例子就是上面那个程序中的：

ylabel('$p=frac{5^{x}}{x!}e^{-5}$','Interpreter','latex','FontSize',15)

3、可以求最值

x=0:1:20

p=poisspdf(x,6)

[ans,pos]=max(p)%取x=pos时，ans取最大

答案：

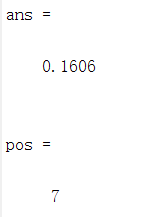
泊松分布与二项分布：

当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ=np(就是数学期望）。

通常当

时，就可以用泊松公式近似的计算。

这一节我们说了说泊松分布与二项分布的相关内容，下一节的内容暂时还没有想好，如果可以的话我们说说matlab中的gui编程

欢迎喜欢的朋友点赞关注收藏啊：）