4.6 统计作图
4.6.1 正整数的频率表
命令 正整数的频率表
函数 tabulate
格式 table = tabulate(X) %X为正整数构成的向量,返回3列:第1列中包含X的值第2列为这些值的个数,第3列为这些值的频率。
例4-49
>> A=[1 2 2 5 6 38]
A =
1 2 2 5 6 3 8
>> tabulate(A)
Value Count Percent
1 1 14.29%
2 2 28.57%
3 1 14.29%
4 0 0.00%
5 1 14.29%
6 1 14.29%
7 0 0.00%
8 1 14.29%
4.6.2 经验累积分布函数图形
函数 cdfplot
格式 cdfplot(X) %作样本X(向量)的累积分布函数图形
h = cdfplot(X) %h表示曲线的环柄
[h,stats] = cdfplot(X) %stats表示样本的一些特征
例4-50
>> X=normrnd(0,1,50,1);
>>[h,stats]=cdfplot(X)
h =
3.0013
stats =
min: -1.8740 %样本最小值
max: 1.6924 %最大值
mean: 0.0565 %平均值
median: 0.1032 %中间值
std: 0.7559 %样本标准差
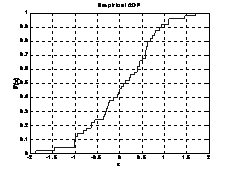
图 4-10
4.6.3 最小二乘拟合直线
函数 lsline
格式 lsline %最小二乘拟合直线
h = lsline %h为直线的句柄
例4-51
>> X = [2 3.4 5.6 8 1112.3 13.8 16 18.8 19.9]';
>> plot(X,'+')
>> lsline
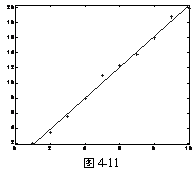
4.6.4 绘制正态分布概率图形
函数 normplot
格式 normplot(X) %若X为向量,则显示正态分布概率图形,若X为矩阵,则显示每一列的正态分布概率图形。
h = normplot(X) %返回绘图直线的句柄
说明 样本数据在图中用“+”显示;如果数据来自正态分布,则图形显示为直线,而其它分布可能在图中产生弯曲。
例4-53
>>X=normrnd(0,1,50,1);
>> normplot(X)
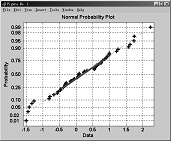
图4-12
4.6.5 绘制威布尔(Weibull)概率图形
函数 weibplot
格式 weibplot(X) %若X为向量,则显示威布尔(Weibull)概率图形,若X为矩阵,则显示每一列的威布尔概率图形。
h = weibplot(X) %返回绘图直线的柄
说明绘制威布尔(Weibull)概率图形的目的是用图解法估计来自威布尔分布的数据X,如果X是威布尔分布数据,其图形是直线的,否则图形中可能产生弯曲。
例4-54
>> r =weibrnd(1.2,1.5,50,1);
>> weibplot(r)
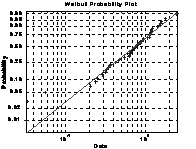
图4-13
4.6.6 样本数据的盒图
函数 boxplot
格式 boxplot(X) %产生矩阵X的每一列的盒图和“须”图,“须”是从盒的尾部延伸出来,并表示盒外数据长度的线,如果“须”的外面没有数据,则在“须”的底部有一个点。
boxplot(X,notch) %当notch=1时,产生一凹盒图,notch=0时产生一矩箱图。
boxplot(X,notch,'sym') %sym表示图形符号,默认值为“+”。
boxplot(X,notch,'sym',vert) %当vert=0时,生成水平盒图,vert=1时,生成竖直盒图(默认值vert=1)。
boxplot(X,notch,'sym',vert,whis)%whis定义“须”图的长度,默认值为1.5,若whis=0则boxplot函数通过绘制sym符号图来显示盒外的所有数据值。
例4-55
>>x1 =normrnd(5,1,100,1);
>>x2 =normrnd(6,1,100,1);
>>x = [x1 x2];
>>boxplot(x,1,'g+',1,0)
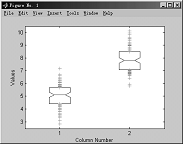
图4-14
4.6.7 给当前图形加一条参考线
函数 refline
格式 refline(slope,intercept) % slope表示直线斜率,intercept表示截距
refline(slope) slope=[a b],图中加一条直线:y=b+ax。
例4-56
>>y = [3.2 2.6 3.1 3.42.4 2.9 3.0 3.3 3.2 2.1 2.6]';
>>plot(y,'+')
>>refline(0,3)
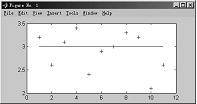
图4-15
4.6.8 在当前图形中加入一条多项式曲线
函数 refcurve
格式 h = refcurve(p) %在图中加入一条多项式曲线,h为曲线的环柄,p为多项式系数向量,p=[p1,p2,p3,…,pn],其中p1为最高幂项系数。
例4-57火箭的高度与时间图形,加入一条理论高度曲线,火箭初速为100m/秒。
>>h = [85 162 230 289339 381 413 437 452 458 456 440 400 356];
>>plot(h,'+')
>>refcurve([-4.9 1000])
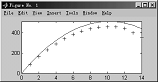
图4-16
4.6.9 样本的概率图形
函数 capaplot
格式 p = capaplot(data,specs)�ta为所给样本数据,specs指定范围,p表示在指定范围内的概率。
说明 该函数返回来自于估计分布的随机变量落在指定范围内的概率
例4-58
>> data=normrnd(0,1,30,1);
>>p=capaplot(data,[-2,2])
p =
0.9199
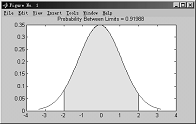
图4-17
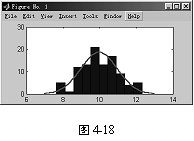
4.6.10 附加有正态密度曲线的直方图
函数 histfit
格式 histfit(data) �ta为向量,返回直方图
和正态曲线。
histfit(data,nbins) % nbins指定bar的个数,
缺省时为data中数据个数的平方根。
例4-59
>>r = normrnd(10,1,100,1);
>>histfit(r)
4.6.11 在指定的界线之间画正态密度曲线
函数 normspec
格式 p = normspec(specs,mu,sigma)%specs指定界线,mu,sigma为正态分布的参数p 为样本落在上、下界之间的概率。
例4-60
>>normspec([10Inf],11.5,1.25)
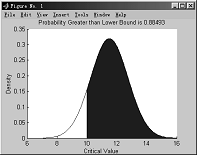
图4-19
4.7 参数估计
4.7.1 常见分布的参数估计
命令 β分布的参数a和b的最大似然估计值和置信区间
函数 betafit
格式 PHAT=betafit(X)
[PHAT,PCI]=betafit(X,ALPHA)
说明 PHAT为样本X的β分布的参数a和b的估计量
PCI为样本X的β分布参数a和b的置信区间,是一个2×2矩阵,其第1例为参数a的置信下界和上界,第2例为b的置信下界和上界,ALPHA为显著水平,(1-α)×100%为置信度。
例4-61 随机产生100个β分布数据,相应的分布参数真值为4和3。则4和3的最大似然估计值和置信度为99%的置信区间为:
解:
>>X = betarnd(4,3,100,1); %产生100个β分布的随机数
>>[PHAT,PCI] =betafit(X,0.01) %求置信度为99%的置信区间和参数a、b的估计值
结果显示
PHAT =
3.9010 2.6193
PCI =
2.5244 1.7488
5.2776 3.4898
说明 估计值3.9010的置信区间是[2.5244 5.2776],估计值2.6193的置信区间是[1.7488 3.4898]。
命令 正态分布的参数估计
函数 normfit
格式 [muhat,sigmahat,muci,sigmaci] = normfit(X)
[muhat,sigmahat,muci,sigmaci] = normfit(X,alpha)
说明 muhat,sigmahat分别为正态分布的参数μ和σ的估计值,muci,sigmaci分别为置信区间,其置信度为;alpha给出显著水平α,缺省时默认为0.05,即置信度为95%。
例4-62 有两组(每组100个元素)正态随机数据,其均值为10,均方差为2,求95%的置信区间和参数估计值。
解:>>r = normrnd(10,2,100,2); %产生两列正态随机数据
>>[mu,sigma,muci,sigmaci] =normfit(r)
则结果为
mu =
10.1455 10.0527 %各列的均值的估计值
sigma =
1.9072 2.1256 %各列的均方差的估计值
muci =
9.7652 9.6288
10.5258 10.4766
sigmaci =
1.6745 1.8663
2.2155 2.4693
说明 muci,sigmaci中各列分别为原随机数据各列估计值的置信区间,置信度为95%。
例4-63 分别使用金球和铂球测定引力常数
(1)用金球测定观察值为:6.683 6.681 6.676 6.678 6.6796.672
(2)用铂球测定观察值为:6.661 6.661 6.667 6.6676.664
设测定值总体为,μ和σ为未知。对(1)、(2)两种情况分别求μ和σ的置信度为0.9的置信区间。
解:建立M文件:LX0833.m
X=[6.683 6.681 6.676 6.678 6.679 6.672];
Y=[6.661 6.661 6.667 6.667 6.664];
[mu,sigma,muci,sigmaci]=normfit(X,0.1) %金球测定的估计
[MU,SIGMA,MUCI,SIGMACI]=normfit(Y,0.1) %铂球测定的估计
运行后结果显示如下:
mu =
6.6782
sigma =
0.0039
muci =
6.6750
6.6813
sigmaci =
0.0026
0.0081
MU =
6.6640
SIGMA =
0.0030
MUCI =
6.6611
6.6669
SIGMACI =
0.0019
0.0071
由上可知,金球测定的μ估计值为6.6782,置信区间为[6.6750,6.6813];
σ的估计值为0.0039,置信区间为[0.0026,0.0081]。
泊球测定的μ估计值为6.6640,置信区间为[6.6611,6.6669];
σ的估计值为0.0030,置信区间为[0.0019,0.0071]。
命令 利用mle函数进行参数估计
函数 mle
格式 phat=mle %返回用dist指定分布的最大似然估计值
[phat, pci]=mle %置信度为95%
[phat, pci]=mle %置信度由alpha确定
[phat, pci]=mle %仅用于二项分布,pl为试验次数。
说明 dist为分布函数名,如:beta(分布)、bino(二项分布)等,X为数据样本,alpha为显著水平α,为置信度。
例4-64
>> X=binornd(20,0.75)%产生二项分布的随机数
X =
16
>>[p,pci]=mle('bino',X,0.05,20) %求概率的估计值和置信区间,置信度为95%
p =
0.8000
pci =
0.5634
0.9427
常用分布的参数估计函数
| 函数名 | 调 用 形 式 | 函 数 说 明 |
| binofit | PHAT= binofit(X, N) [PHAT, PCI] = binofit(X,N) [PHAT, PCI]= binofit (X, N, ALPHA) | 二项分布的概率的最大似然估计 置信度为95%的参数估计和置信区间 返回水平α的参数估计和置信区间 |
| poissfit | Lambdahat=poissfit(X) [Lambdahat, Lambdaci] = poissfit(X) [Lambdahat, Lambdaci]= poissfit (X, ALPHA) | 泊松分布的参数的最大似然估计 置信度为95%的参数估计和置信区间 返回水平α的λ参数和置信区间 |
| normfit | [muhat,sigmahat,muci,sigmaci] = normfit(X) [muhat,sigmahat,muci,sigmaci] = normfit(X,ALPHA) | 正态分布的最大似然估计,置信度为95% 返回水平α的期望、方差值和置信区间 |
| betafit | PHAT =betafit (X) [PHAT, PCI]= betafit (X, ALPHA) | 返回β分布参数a和 b的最大似然估计 返回最大似然估计值和水平α的置信区间 |
| unifit | [ahat,bhat] = unifit(X) [ahat,bhat,ACI,BCI] = unifit(X) [ahat,bhat,ACI,BCI]=unifit(X, ALPHA) | 均匀分布参数的最大似然估计 置信度为95%的参数估计和置信区间 返回水平α的参数估计和置信区间 |
| expfit | muhat =expfit(X) [muhat,muci] = expfit(X) [muhat,muci] = expfit(X,alpha) | 指数分布参数的最大似然估计 置信度为95%的参数估计和置信区间 返回水平α的参数估计和置信区间 |
| gamfit | phat =gamfit(X) [phat,pci] = gamfit(X) [phat,pci] = gamfit(X,alpha) | γ分布参数的最大似然估计 置信度为95%的参数估计和置信区间 返回最大似然估计值和水平α的置信区间 |
| weibfit | phat = weibfit(X) [phat,pci] = weibfit(X) [phat,pci] = weibfit(X,alpha) | 韦伯分布参数的最大似然估计 置信度为95%的参数估计和置信区间 返回水平α的参数估计及其区间估计 |
| Mle | phat = mle('dist',data) [phat,pci] = mle('dist',data) [phat,pci] = mle('dist',data,alpha) [phat,pci] = mle('dist',data,alpha,p1) | 分布函数名为dist的最大似然估计 置信度为95%的参数估计和置信区间 返回水平α的最大似然估计值和置信区间 仅用于二项分布,pl为试验总次数 |
说明 各函数返回已给数据向量X的参数最大似然估计值和置信度为(1-α)×100%的置信区间。α的默认值为0.05,即置信度为95%。
4.7.2 非线性模型置信区间预测
命令 高斯—牛顿法的非线性最小二乘数据拟合
函数 nlinfit
格式 beta = nlinfit(X,y,FUN,beta0) %返回在FUN中描述的非线性函数的系数。FUN为用户提供形如的函数,该函数返回已给初始参数估计值β和自变量X的y的预测值。
[beta,r,J] = nlinfit(X,y,FUN,beta0)�ta为拟合系数,r为残差,J为Jacobi矩阵,beta0为初始预测值。
说明 若X为矩阵,则X的每一列为自变量的取值,y是一个相应的列向量。如果FUN中使用了@,则表示函数的柄。
例4-65 调用MATLAB提供的数据文件reaction.mat
>>load reaction
>>betafit =nlinfit(reactants,rate,@hougen,beta)
betafit =
1.2526
0.0628
0.0400
0.1124
1.1914
命令 非线性模型的参数估计的置信区间
函数 nlparci
格式 ci = nlparci(beta,r,J) %返回置信度为95%的置信区间,beta为非线性最小二乘法估计的参数值,r为残差,J为Jacobian矩阵。nlparci可以用nlinfit函数的输出作为其输入。
例4-66 调用MATLAB中的数据reaction。
>>load reaction
>>[beta,resids,J] =nlinfit(reactants,rate,'hougen',beta)
beta =
1.2526
0.0628
0.0400
0.1124
1.1914
resids =
0.1321
-0.1642
-0.0909
0.0310
0.1142
0.0498
-0.0262
0.3115
-0.0292
0.1096
0.0716
-0.1501
-0.3026
J =
6.8739 -90.6536 -57.8640 -1.9288 0.1614
3.4454 -48.5357 -13.6240 -1.7030 0.3034
5.3563 -41.2099 -26.3042 -10.5217 1.5095
1.6950 0.1091 0.0186 0.0279 1.7913
2.2967 -35.5658 -6.0537 -0.7567 0.2023
11.8670 -89.5655 -170.1745 -8.9566 0.4400
4.4973 -14.4262 -11.5409 -9.3770 2.5744
4.1831 -41.7896 -16.8937 -5.7794 1.0082
11.8286 -51.3721 -154.1164 -27.7410 1.5001
9.1514 -25.5948 -76.7844 -30.7138 2.5790
3.3373 0.0900 0.0720 0.1080 3.5269
9.3663 -102.0611 -107.4327 -3.5811 0.2200
4.7512 -24.4631 -16.3087 -10.3002 2.1141
>>ci =nlparci(beta,resids,J)
ci =
-0.7467 3.2519
-0.0377 0.1632
-0.0312 0.1113
-0.0609 0.2857
-0.7381 3.1208
命令 非线性拟合和显示交互图形
函数 nlintool
格式 nlintool(x,y,FUN,beta0) %返回数据(x,y)的非线性曲线的预测图形,它用2条红色曲线预测全局置信区间。beta0为参数的初始预测值,置信度为95%。
nlintool(x,y,FUN,beta0,alpha) %置信度为(1-alpha)×100%
例4-67 调用MATLAB数据
>> load reaction
>>nlintool(reactants,rate,'hougen',beta)
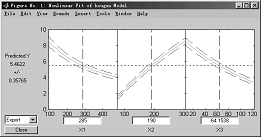
图4-20
命令 非线性模型置信区间预测
函数 nlpredci
格式 ypred = nlpredci(FUN,inputs,beta,r,J) % ypred为预测值,FUN与前面相同,beta为给出的适当参数,r为残差,J为Jacobian矩阵,inputs为非线性函数中的独立变量的矩阵值。
[ypred,delta] = nlpredci(FUN,inputs,beta,r,J)�lta为非线性最小二乘法估计的置信区间长度的一半,当r长度超过beta的长度并且J的列满秩时,置信区间的计算是有效的。[ypred-delta,ypred+delta]为置信度为95%的不同步置信区间。
ypred =nlpredci(FUN,inputs,beta,r,J,alpha,'simopt','predopt')%控制置信区间的类型,置信度为100(1-alpha)%。'simopt' = 'on' 或'off' (默认值)分别表示同步或不同步置信区间。'predopt'='curve'(默认值) 表示输入函数值的置信区间, 'predopt'='observation'表示新响应值的置信区间。nlpredci可以用nlinfit函数的输出作为其输入。
例4-68 续前例,在[100 300 80]处的预测函数值ypred和置信区间一半宽度delta
>> load reaction
>> [beta,resids,J] =nlinfit(reactants,rate,@hougen,beta);
>> [ypred,delta] =nlpredci(@hougen,[100 300 80],beta,resids,J)
结果为:
ypred =
10.9113
delta =
0.3195
命令 非负最小二乘
函数 nnls(该函数已被函数lsnonneg代替,在6.0版中使用nnls将产生警告信息)
格式 x = nnls(A,b) %最小二乘法判断方程A×x=b的解,返回在x≥0的条件下使得最小的向量x,其中A和b必须为实矩阵或向量。
x = nnls(A,b,tol) % tol为指定的误差
[x,w] = nnls(A,b) %当x中元素时,,当时。
[x,w] = nnls(A,b,tol)
例4-69
>> A =[0.03720.2869;0.6861 0.7071;0.6233 0.6245;0.6344 0.6170];
>> b=[0.8587 0.17810.0747 0.8405]';
>> x=nnls(A,b)
Warning: NNLS is obsolete and has been replaced byLSQNONNEG.
NNLS now calls LSQNONNEG which uses the followingsyntax:
[X,RESNORM,RESIDUAL,EXITFLAG,OUTPUT,LAMBDA]
=lsqnonneg(A,b,X0, Options) ;
Use OPTIMSET to define optimization options, ortype
'edit nnls' to view the code used here. NNLS willbe
removed in the future; please use NNLS with the newsyntax.
x =
0
0.6929
命令 有非负限制的最小二乘
函数 lsqnonneg
格式 x = lsqnonneg(C,d) %返回在x≥0的条件下使得最小的向量x,其中C和d必须为实矩阵或向量。
x = lsqnonneg(C,d,x0) % x0为初始点,x0≥0
x = lsqnonneg(C,d,x0,options) %options为指定的优化参数,参见options函数。
[x,resnorm] = lsqnonneg(…) %resnorm表示norm(C*x-d).^2的残差
[x,resnorm,residual] = lsqnonneg(…) %residual表示C*x-d的残差
例4-70
>> A =[0.03720.2869;0.6861 0.7071;0.6233 0.6245;0.6344 0.6170];
>> b=[0.8587 0.17810.0747 0.8405]';
>>[x,resnorm,residual] = lsqnonneg(A,b)
x =
0
0.6929
resnorm =
0.8315
residual =
0.6599
-0.3119
-0.3580
0.4130
4.7.3 对数似然函数
命令 负分布的对数似然函数
函数 Betalike
格式 logL=betalike(params,data)%返回负分布的对数似然函数,params为向量[a, b],是分布的参数,data为样本数据。
[logL,info]=betalike(params,data) %返回Fisher逆信息矩阵info。如果params 中输入的参数是极大似然估计值,那么info的对角元素为相应参数的渐近方差。
说明 betalike是分布最大似然估计的实用函数。似然函数假设数据样本中,所有的元素相互独立。因为betalike返回负对数似然函数,用fmins函数最小化betalike与最大似然估计的功能是相同的。
例4-71 本例所取的数据是随机产生的分布数据。
>>r =betarnd(3,3,100,1);
>>[logL,info] =betalike([2.1234,3.4567],r)
logL =
-12.4340
info =
0.1185 0.1364
0.1364 0.2061
命令 负分布的对数似然估计
函数 Gamlike
格式 logL=gamlike(params,data) %返回由给定样本数据data确定的分布的参数为params(即[a,b])的负对数似然函数值
[logL,info]=gamlike(params,data) %返回Fisher逆信息矩阵info。如果params中输入的参数是极大似然估计值,那么info的对角元素为相应参数的渐近方差。
说明 gamlike是分布的最大似然估计函数。因为gamlike返回对数似然函数值,故用fmins函数将gamlike最小化后,其结果与最大似然估计是相同的。
例4-72
>>r=gamrnd(2,3,100,1);
>>[logL,info]=gamlike([2.4212,2.5320],r)
logL =
275.4602
info =
0.0453 -0.0538
-0.0538 0.0867
命令 负正态分布的对数似然函数
函数 normlike
格式 logL=normlike(params,data) %返回由给定样本数据data确定的、负正态分布的、参数为params(即[mu,sigma])的对数似然函数值。
[logL,info]=normlike(params,data) %返回Fisher逆信息矩阵info。如果params中输入的参数是极大似然估计值,那么info的对角元素为相应参数的渐近方差。
命令 威布尔分布的对数似然函数
函数 Weiblike
格式 logL = weiblike(params,data) %返回由给定样本数据data确定的、威布尔分布的、参数为params(即[a,b])的对数似然函数值。
[logL,info]=weiblike(params,data)%返回Fisher逆信息矩阵info。如果params中输入的参数是极大似然估计值,那么info的对角元素为相应参数的渐近方差。
说明 威布尔分布的负对数似然函数定义为
例4-73
>>r=weibrnd(0.4,0.98,100,1);
>>[logL,info]=weiblike([0.1342,0.9876],r)
logL =
237.6682
info =
0.0004 -0.0002
-0.0002 0.0078
最后
以上就是大方小蝴蝶最近收集整理的关于MATLAB各种概率分布统计分析画图的全部内容,更多相关MATLAB各种概率分布统计分析画图内容请搜索靠谱客的其他文章。








发表评论 取消回复