1.poissrnd()
语句r = poissrnd(lambda)生成随机数,其服从参数为λ(lambda)的泊松分布。
λ可以是标量、向量、矩阵或多维数组。
r = poissrnd(lambda)
r = poissrnd(lambda,sz1,…,szN)
r = poissrnd(lambda,[sz1,…,szN])
example1:
r = poissrnd(10);
r = 16example2:
r = poissrnd(10,1,2,3);
val(:,:,1) =
11 9
val(:,:,2) =
8 9
val(:,:,3) =
12 9
example3:
r = poissrnd(10,[1,2,3]);val(:,:,1) =
10 8
val(:,:,2) =
6 8
一般来说,我们写成类似data = poissrnd(200,1,700);即可,表示生成1X700数组(即700个数)的符合λ=200的随机数

2.ksdensity()函数
用于计算一维或二维核密度或分布估计。其主要使用格式:
[F,XI]=ksdensity(X) %计算的概率密度估计在向量或两列的矩阵X (ksdensity样本)评价
100点密度估计(或二元数据的900点密度估计)的数据。
式中:F——密度值的向量。;XI——100(或900)点的集合。(也就是说可以对x这个数组,进行每个点的概率分析)
[f,xi]=ksdensity(data);
figure(2);
plot(xi,f);
xlabel('xi'),ylabel('f');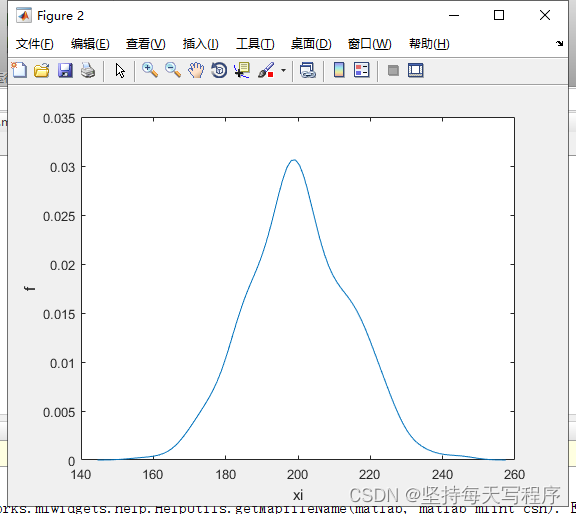
3.poissfit()
泊松参数估计
lambdahat = poissfit(data) 基于给定数据 data 返回泊松分布参数 λ 的最大似然估计 (MLE) 值。
[lambdahat,lambdaci] = poissfit(data) 还在 lambdaci 中给出 95% 的置信区间。
[lambdahat,lambdaci] = poissfit(data,alpha) 给出 100(1 - alpha)% 的置信区间。例如,alpha = 0.001 得出 99.9% 的置信区间。
样本均值是 λ 的 MLE。
ˆλ=1nn∑i=1xi
[mu,sigma]= poissfit(data);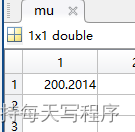
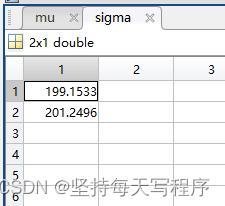
4.实际示例:
x = 1:700;
data = poissrnd(200,1,700); %生成700个 参数为200的符合泊松分布的数据
figure(1);
plot(x,data);%画出700个数据的参数图
[f,xi]=ksdensity(data); %生成700个数据的概率分布图
figure(2);
plot(xi,f);
xlabel('xi'),ylabel('f');
[mu,sigma]= poissfit(data); %分析是否符合泊松分布
fid = fopen('data.coe','wt'); %将生成的数据保存到.coe文件中
fprintf(fid,'memory_initialization_radix=10;n',data); %这两行是保存为coe文件必须写的,如果是mif文件就不需要
%文件存储数据的进制,10即为10进制
fprintf(fid,'memory_initialization_vector=n',data);
fprintf(fid,'%g,n',data);
fclose(fid);
fid = fopen('data.mif','wt'); %将生成的数据保存到.mif文件中
fprintf(fid,'%g,n',data);
fclose(fid);其中输出coe文件时,必须加上两行
fprintf(fid,'memory_initialization_radix=10;n',data);
fprintf(fid,'memory_initialization_vector=n',data);
memory_initialization_radix表示内存初始化基数,即初始化数据类型,有效值为2(表示二进制),10(表示十进制),16(表示十六进制)。
memory_initialization_vector表示内存初始化向量,用来定义每个内存的内容
下面是coe文件输出的结果:
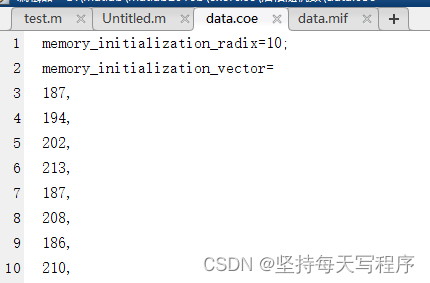
下面是mif文件输出的格式

5.将生成数据的概率分布和拟合的泊松分布的概率分布进行对比
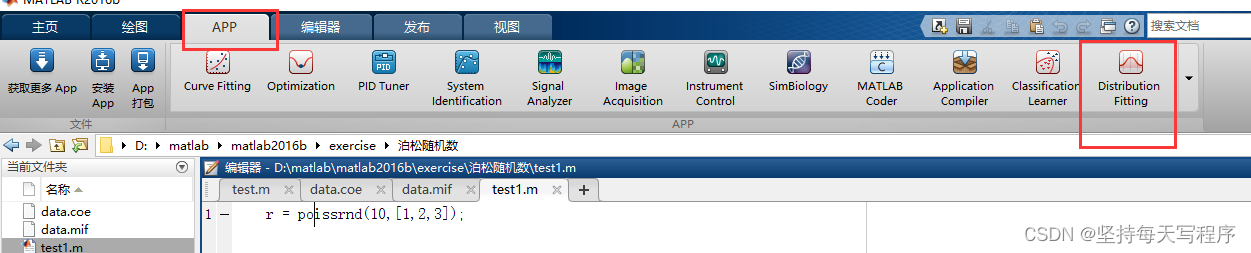
选择pdf,然后点击data: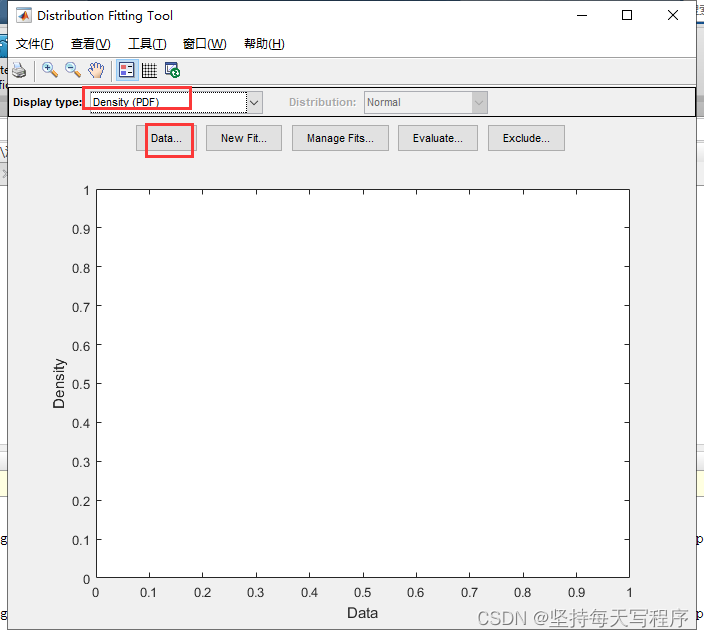
选择生成的数据
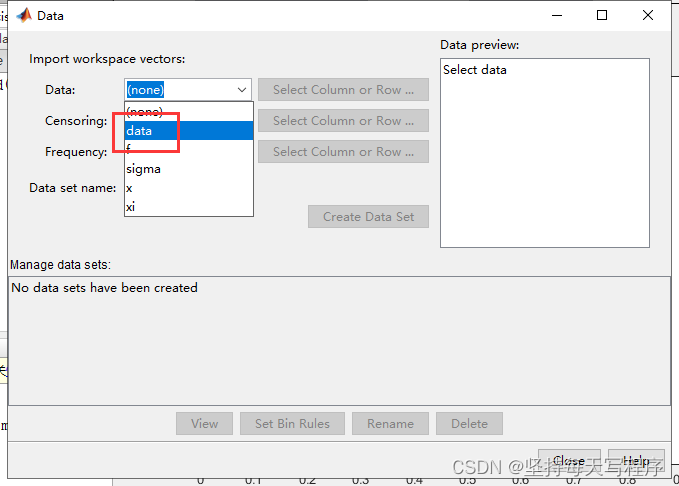
点击创建data:
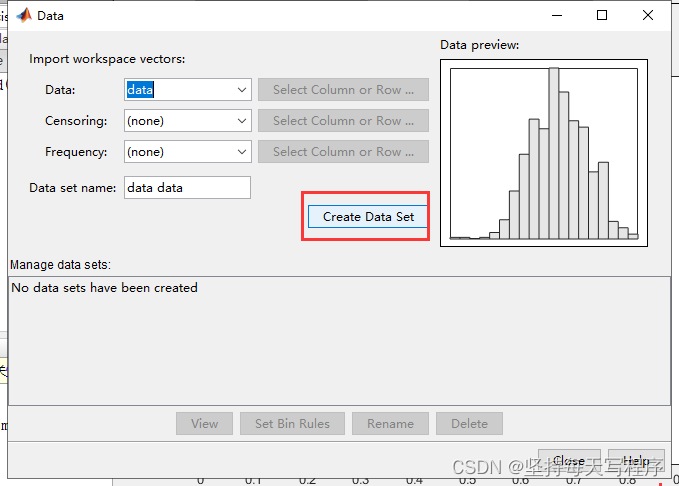
点击view,就可以看到数据直方图:
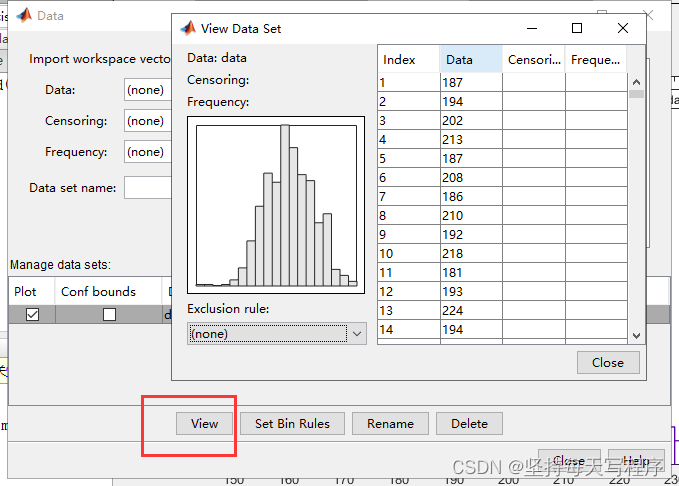
关闭回到设置页面,点击new fit:
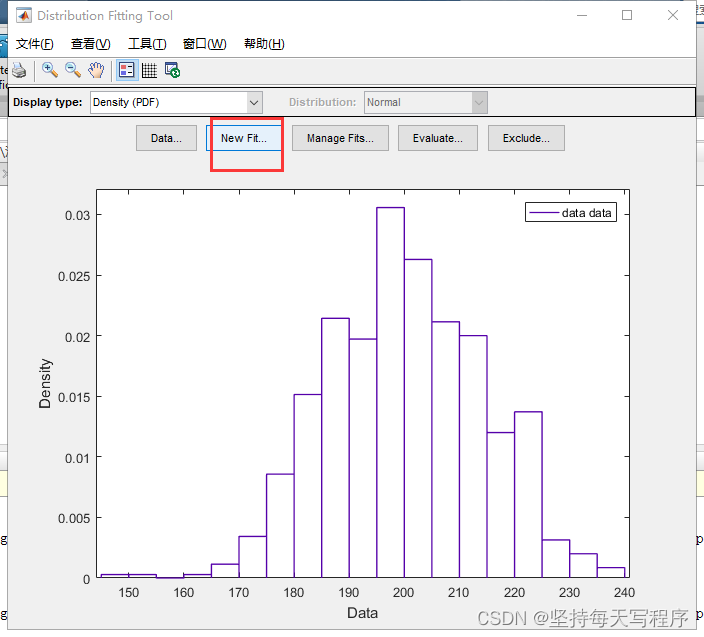
然后选择我们需要的泊松类型,然后点击apply,然后点击close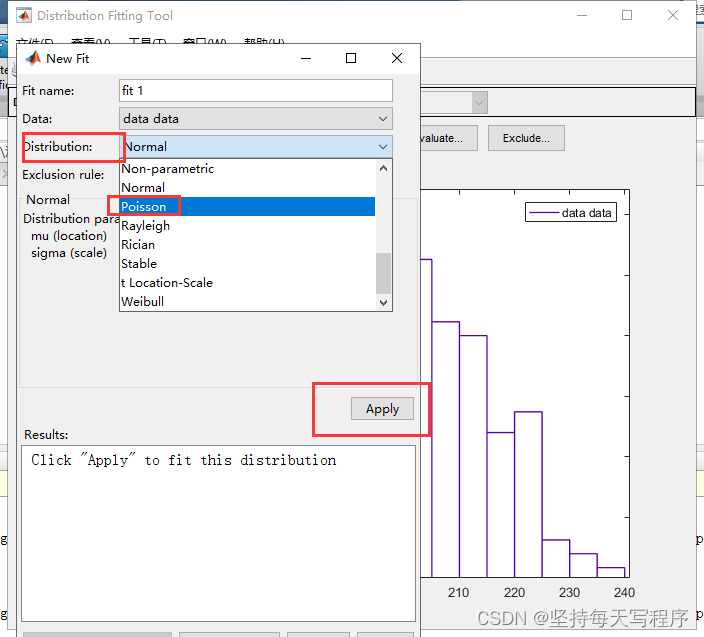
就可以得到泊松分布的拟合曲线:
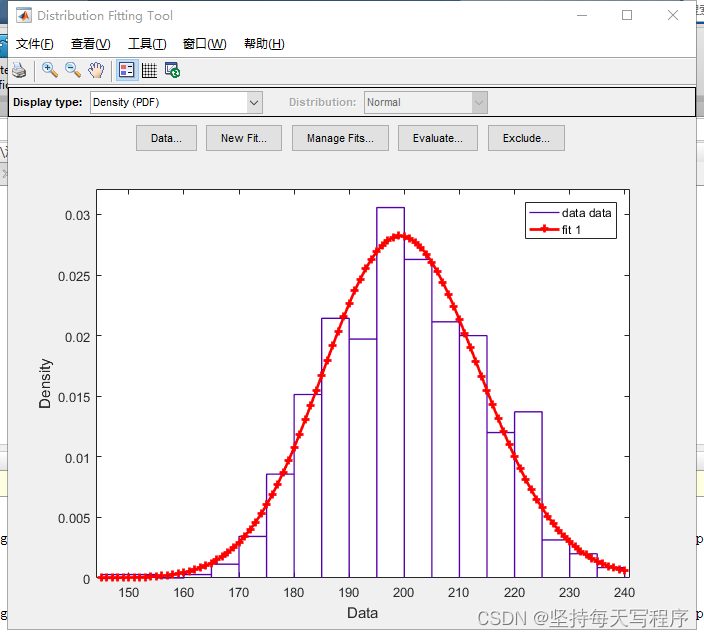
可以看到红色的泊松分布曲线和我们生成的数据的概率分布是基本吻合的,所以生成的随机数满足泊松分布。
6.工程链接:https://download.csdn.net/download/qq_43811597/86475770
最后
以上就是眼睛大战斗机最近收集整理的关于matalb生成符合泊松分布的随机数,并进行测试是否符合1.poissrnd()2.ksdensity()函数 3.poissfit() 4.实际示例: 5.将生成数据的概率分布和拟合的泊松分布的概率分布进行对比6.工程链接:https://download.csdn.net/download/qq_43811597/86475770的全部内容,更多相关matalb生成符合泊松分布内容请搜索靠谱客的其他文章。








发表评论 取消回复