matlab符号计算求解正态分布问题

举个栗子：

此问题已给出平均分（均值μ）和标准差（即σ），所以已知X~N(μ, σ^2)
所以可以根据f(x)=(1/(sqrt(2*pi)*σ))exp(-((x-σ)^2/2σσ))写出其概率函数。并对其在特定范围求定积分可以求得概率，进而求得人数。
Matlab程序如下：

close all;
clear ;
clc;
% MATLAB演示正态分布特征的方法
% 正态分布(Normal Distribution):X~N(u,σ^2)
u = 57.08; %平均值即期望
d = 18.04; %标准差即sigma
n=47000; %样本总数
format long

syms x y; % 定义符号
f(x)= 1/(sqrt(2pi)d)exp(-(x-u).^2/(2*d2)); % 代入概率密度函数
k1=int(f,x,0,100); % 求函数f对符号变量x从1到2的定积分
y=double(k1); % 将符号解转为数值解
%disp(k1); % 输出k1值
%disp(y); % 输出y值
disp("**********************")

%%
%验算1sigma
syms x y; % 定义符号
f(x)= 1/(sqrt(2pi)d)exp(-(x-u).^2/(2*d2)); % 代入概率密度函数
k1=int(f,x,57.08-18.04,57.08+18.04); % 求函数f对符号变量x从1到2的定积分
y=double(k1); % 将符号解转为数值解
%disp(k1); % 输出k1值
disp(y); % 输出y值
num = ny %求出人数
disp("************************")

%%
%验算2sigma
syms x y; % 定义符号
f(x)= 1/(sqrt(2pi)d)exp(-(x-u).^2/(2*d2)); % 代入概率密度函数
k1=int(f,x,57.08-218.04,57.08+218.04); % 求函数f对符号变量x从1到2的定积分
y=double(k1); % 将符号解转为数值解
%disp(k1); % 输出k1值
disp(y); % 输出y值
num = ny %求出人数
disp("************************")

%%
%求解第一问
syms x y; % 定义符号
f(x)= 1/(sqrt(2pi)d)exp(-(x-u).^2/(2*d2)); % 代入概率密度函数
k1=int(f,x,0,60); % 求函数f对符号变量x从1到2的定积分
y=double(k1); % 将符号解转为数值解
%disp(k1); % 输出k1值
disp(y); % 输出y值
num = ny %求出人数
disp("***********************")

%%
%求解第二问
syms x y; % 定义符号
f(x)= 1/(sqrt(2pi)d)exp(-(x-u).^2/(2*d2)); % 代入概率密度函数
k1=int(f,x,80,90); % 求函数f对符号变量x从1到2的定积分
y=double(k1); % 将符号解转为数值解
%disp(k1); % 输出k1值
disp(y); % 输出y值
num = ny %求出人数
disp("***********************")

%%
%求解第三问
syms x y; % 定义符号
f(x)= 1/(sqrt(2pi)d)exp(-(x-u).^2/(2*d2)); % 代入概率密度函数
k1=int(f,x,90,100); % 求函数f对符号变量x从1到2的定积分
y=double(k1); % 将符号解转为数值解
%disp(k1); % 输出k1值
disp(y); % 输出y值
num = ny %求出人数
disp("***********************")

运行结果如下：

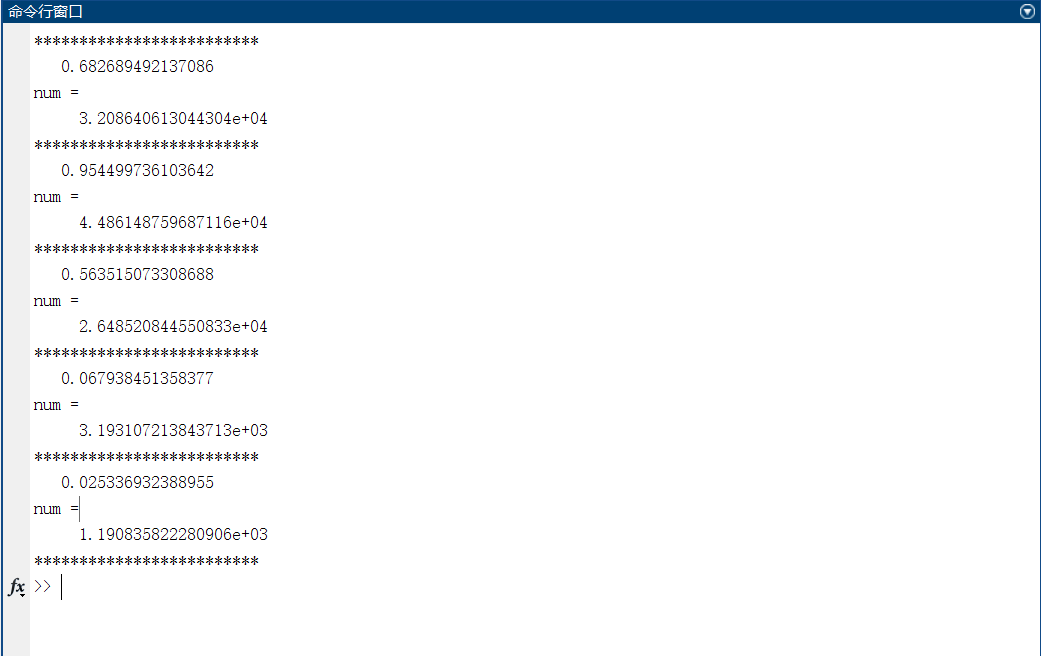
最后

以上就是落寞猎豹为你收集整理的matlab符号计算求解正态分布问题的全部内容，希望文章能够帮你解决matlab符号计算求解正态分布问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。