威布尔分布的参数估计

84 阅读 0 评论 56 点赞

我是靠谱客的博主眼睛大唇彩，最近开发中收集的这篇文章主要介绍威布尔分布的参数估计，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1. 三参数威布尔分布的密度函数和累积密度函数

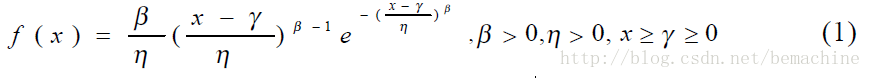
其中gama位置参数，且gama>0; 表示设备在[0, gama]之间不会发生故障

eta是比例参数，表示函数的缩放

beta是形状参数，表示函数的走势，beta>1,表示故障率随时间增加，beta<1, 表示故障率随时间减小

2. 参数估计中的gama估计相对简单，一般取设备开始使用到第一次发生故障的最短时间，所以，所有的故障发生时间减去gama，故障率就服二参数威布尔分布。

所以这里为了简单且不失泛化能力，假设为0.

3. 下面证明beta和eta之间存在线性关系

gama=0，

由（2）得到

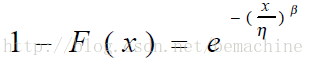
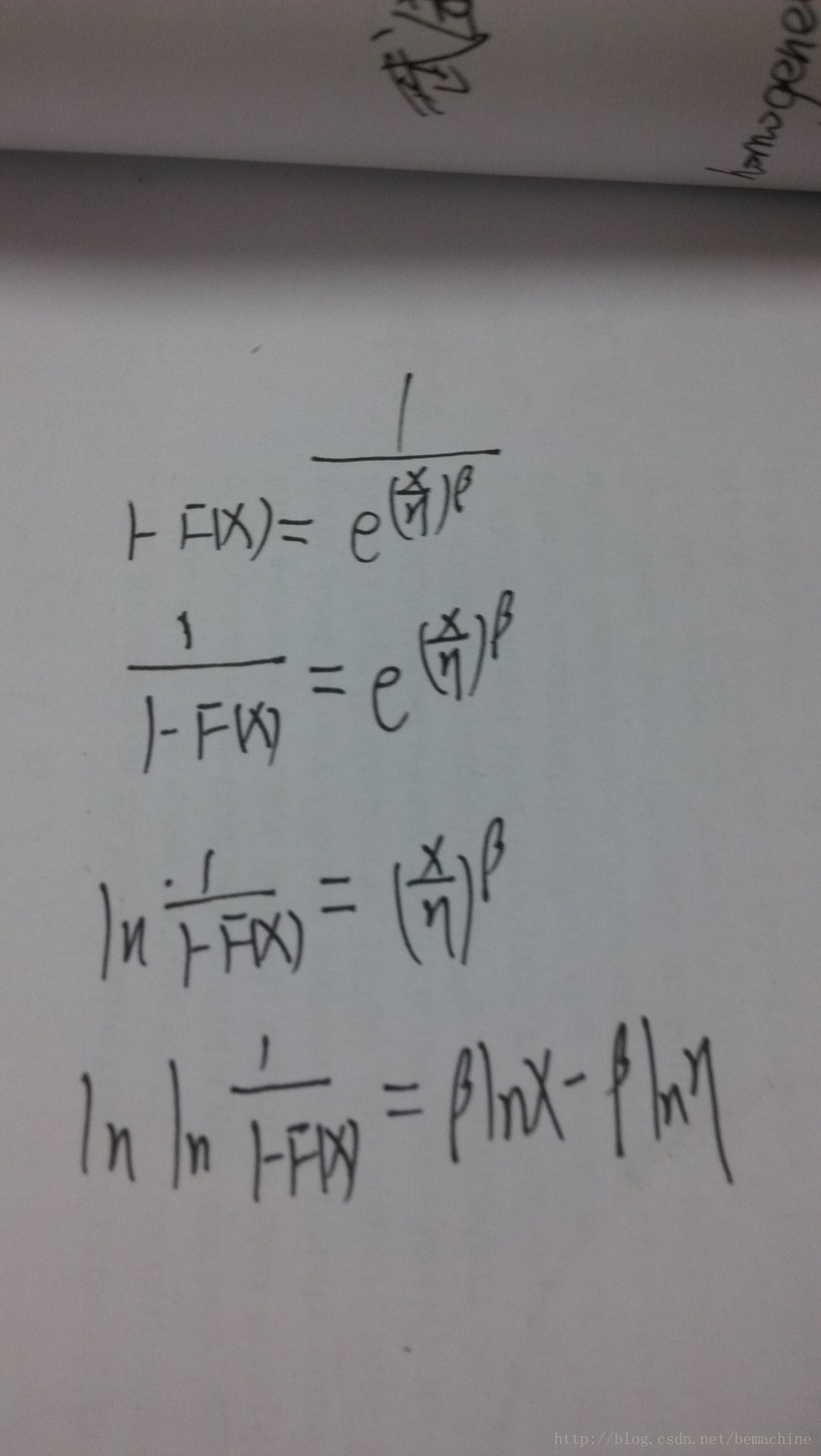
可以看到，最后一个公式是一个与参数有关的直线，所以可以使用线性拟合的方法估计参数。

4. 威布尔分布的参数估计原理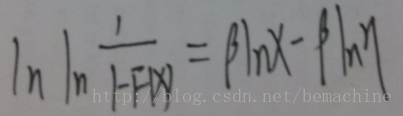

根据上面的讨论，如上式所示，如果我们有一些故障发生的时间点 x, 且知道对应的F(x)的值，就相当于知道了一些二维的数据点，可以用最小二乘法估计beta和eta。

5. X和F(x)的获取

X是设备发生故障的时间点，这可以从故障数据中获得。假如取100次故障发生的时间点，则：

X = [x1,x2,x3,…,x100]

其中x1<x2<x3<…<x100

这里故障发生的时间点是按照时间顺序排列的

同样，F(xi) = P(x<xi)

F(xi)是截止到时间xi,设备发生故障的概率

我们这里认为，F(x1)<F(x2)<…<F(x100),且F(x1)=0, F(x100)=1

那么F(xi)是多少呢？

这里取F(xi)=i/(n+1),基本符合上面的要求

6. 参数估计的过程如下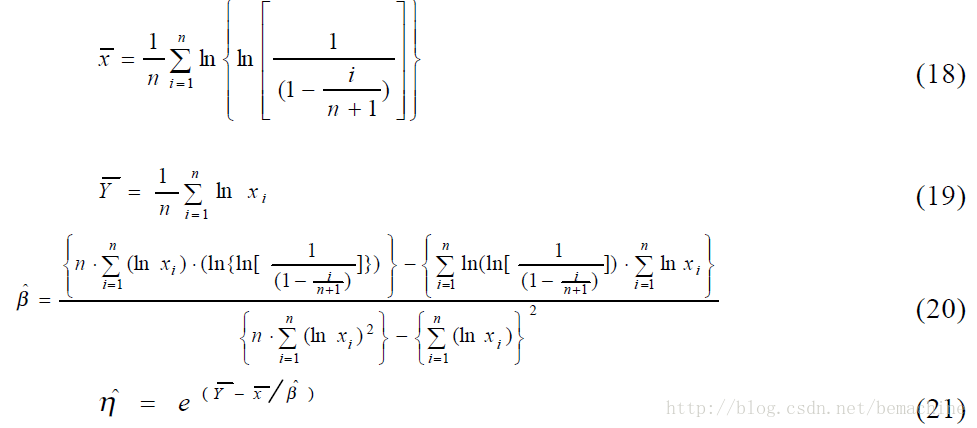

7. 举例

使用matlab的随机生成函数，生成100个服从威布尔分布的时间点

X = wblrnd(1,2,100,1)

这里beta=2， eta=1；

下面按照上面的方法，计算beta和eta，计算结果如下，

beta= 2.05994， eta=0.982495

计算过程参考代码

8. 威布尔参数的估计有多种方法，最小二乘是精度和复杂度折中的方法。

代码如下

// 威布尔.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <iostream>
#include <math.h>
using namespace std;

int main()
{	
	//发生故障的时间
	double time[] = {0.1100,	0.1430,0.1468,0.1939,    0.2509,    0.2717,    0.2823,0.3012,    0.3162,    0.3164,    0.3182,
		0.3398,    0.3471,    0.3493,    0.3639,    0.3892,    0.4114,    0.4569,    0.4651,    0.4710,    0.4774,    0.4997,
		0.5437,    0.5606,    0.5717,    0.5792,    0.5820,    0.5838,    0.5987,    0.6213,    0.6220,    0.6519,    0.6630,
		0.6867,    0.6885,    0.6941,    0.7032,    0.7114,    0.7207,    0.7298,    0.7398,    0.7419,    0.7730,    0.7770,
		0.7934,    0.8073,    0.8231,    0.8320,    0.8325,    0.8396,    0.8447,    0.8459,    0.8463,    0.8568,    0.8676,
		0.8678,    0.8826,    0.9075,    0.9115,    0.9184,    0.9261,    0.9459,    0.9631,    0.9855,    1.0006,    1.0236,    
		1.0453,    1.0470,    1.0692,    1.0806,    1.0954,    1.1023,    1.1565,    1.1570,    1.1575,    1.1638,    1.1947,
		1.1994,    1.2094,    1.2114,    1.2165,    1.2197,    1.2273,    1.2536,    1.2730,    1.2790,    1.2994,    1.3033,
		1.3296,    1.3357,    1.4110,    1.4636,    1.4823,    1.4957,    1.5217,    1.5681,    1.8103,    1.8678,    1.8796,
		1.8846};
	//100个故障点
	int num_point = 100;

	//下面计算文档中对应的公式
	double xmean = 0.0;
	double ymean = 0.0;
	double beta1 = 0.0;
	double beta21 = 0.0;
	double beta22 = 0.0;
	double beta3 = 0.0;
	double beta4 = 0.0;
	double beta2 = 0.0;
	
	for(int i = 0; i < num_point; i++)
	{
		xmean += log(log(1.0/(1-(i+1)*1.0/(num_point+1))));
		ymean += log(time[i]);
		beta1 += log(time[i])*log(log(1.0/(1-(i+1)*1.0/(num_point+1))));
		beta21 += log(log(1.0/(1-(i+1)*1.0/(num_point+1))));
		beta22 += log(time[i]);
		beta3 += log(time[i])*log(time[i]);
		beta4 += log(time[i]);
	}
	ymean = ymean/num_point;
	xmean = xmean/num_point;
	beta1 = beta1 * num_point;
	beta2 = beta21*beta22;
	beta3 = beta3*num_point;
	beta4 = beta4*beta4;
	double beta = (beta1-beta2)/(beta3-beta4);
	double eta = exp(ymean - xmean/beta);
	cout << "beta: " << beta << "eta: " << eta;
	return 0;
}

9.参考文献

Methods for Estimating the Parameters of the Weibull Distribution

Mohammad A. Al-Fawzan